теор вер. Решение Решение
 Скачать 125.32 Kb. Скачать 125.32 Kb.
|
|
Зима Задание 1 Шифр кодового замка состоит из трёх цифр. Найти вероятность того, что: 1) все они различны Решение: Решение. Так как на каждом из 3 мест в шифре может стоять любая из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, то всех различных номеров по правилу произведения будет n=10*10*10=1000. Номера, в которых все цифры различны, - это размещения из 10 элементов (10 цифр) по 3. Поэтому число благоприятствующих исходов m=A310. Искомая вероятность равна 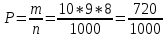 =0.72 =0.722) шифр заканчивается цифрой 7 m=A37=7*6*5=210 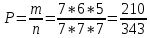 =0.6 =0.6Задание 2 Из 28 костей домино случайно выбирается две. Найти вероятность того, что из них можно составить цепочку составить цепочку согласно правилам игры. Количество вариантов выбора 2 костей равно 28*27=756. Порядок имеет значение. Это используем и дальше. Подсчитаем количество благоприятных случаев (чтобы кости подходили, т.е. совпадало хотя бы по одному значению на обеих костях). Если первая кость дубль, то это 7 вариантов. К ней подходит 6 "не дублей". Всего 7*6=42 Если первая - "не дубль", то таких костей 21. К первому числу подходит 6 костей и ко второму числу 6 костей, значит для первой кости - "не дубль" подходит 12 вариантов, а всего благоприятных исходов 21*12 = 252. Общее кол-во благоприятных исходов 42+252 = 294. Р = 294/756 = 0,388...≈ 0,389 Задание 3 Стрелок произвел три выстрела по мишени. Событие А – попадание в мишень при к-ом выстреле (к=1,2,3). Выразить через А1, А2, А3. Следующие события: А- хотя бы одного попадания Событие (А1+A2+A3) – хотя бы одно попадание в цель. Вероятность хотя бы одного попадания в цель: P(A1+A2+A3)=1-P( 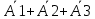 ) )Б –три промаха Вероятность промаха всех стрелков одновременно Р( 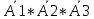 ) )Событиевсе промахнулисьP(Б)= ( 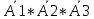 ) )Задание 4 В собираем механизм входят две одинаковые шестерни. Технические условия нарушаются, если обе они оказываются с отклонениями по толщине зуба в положительную сторону от среднего размера (заедание). У сборщика имеется 10 шестерён из которых 3 с плюсовым отклонением. Определить вероятность нарушения технических условий при случайном выборе двух шестерён. 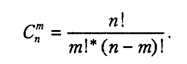 m= 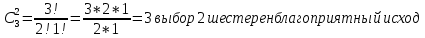 n= 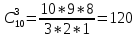 общее число исходов общее число исходовР=m/n=3/120=0.025 Задание 5 Среди облигаций займа половина выигрышных. Сколько облигаций следует взять, чтобы рассчитывать на выигрыш с вероятностью, большей 0.95? Пусть вероятность события Ai– выигрыша по i-мy билету равна р,т.е. P(Ai)= р.Тогда вероятность выигрыша хотя бы по одному из пприобретенных билетов, т.е. вероятность суммы независимых событий A1,A2,...,Ai,...,Anопределится по формуле P(A1+A2+…+An) = 1-(1-p)n По условию 1-(1-p)n ≥ R , где R = 0,95, откуда (1 - p)n ≤ 1 – R Логарифмируя обе части неравенства, имеем nlg(1 - p) ≤ lg(1 - R) Учитывая, что lg(1 - p) – величина отрицательная, получим По условию р = 0,5, R = 0,95. По формуле n 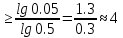 , т.е. n ≥ 4 и необходимо купить не менее 4 лотерейных билетов. Лето ВАРИАНТ 5 Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
Найти: 1) функцию распределения F(x); 2) числовые характеристики: математическое ожидание М(X), дисперсию D(X), среднее квадратическое отклонение (X), моду M0(Х); 3) вероятность P(40 ≤ X < 80). Построить многоугольник распределения и график F(x). Математическое ожидание находим по формуле m = ∑xipi. Математическое ожидание M[X]. M[x] = 20*0.2 + 40*0.1 + 50*0.4 + 70*0.2 + 80*0.1 = 50 Дисперсию находим по формуле d = ∑x2ipi - M[x]2. Дисперсия D[X]. D[X] = 202*0.2 + 402*0.1 + 502*0.4 + 702*0.2 + 802*0.1 - 502 = 360 Среднее квадратическое отклонение σ(x). Мода распределения равна 50 так как P = 0,4 максимально M0(X)=50 Функция распределения F(X). F(x≤20) = 0 F(20< x ≤40) = 0.2 F(40< x ≤50) = 0.1 + 0.2 = 0.3 F(50< x ≤70) = 0.4 + 0.3 = 0.7 F(70< x ≤80) = 0.2 + 0.7 = 0.9 F(x>80) = 1 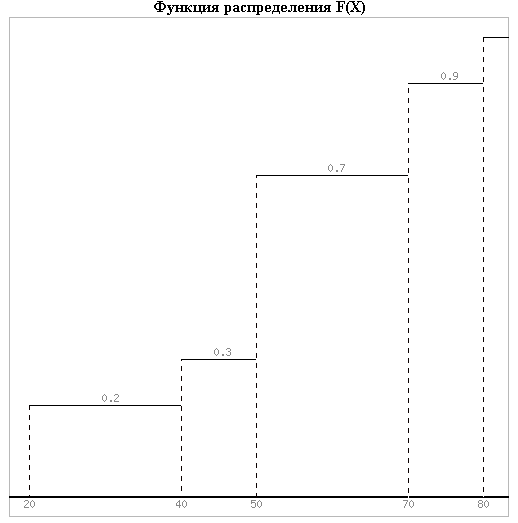 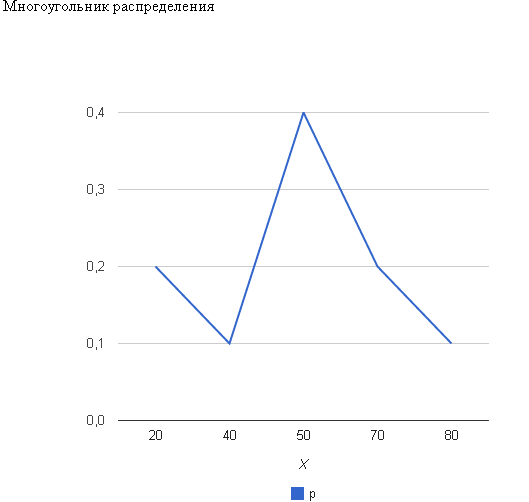 Задача 2. Автоматическая линия состоит из n независимо работающих однотипных станков. Вероятность того, что станок потребует наладки в течение смены для каждого станка равна 0,3. Требуется: 1) построить ряд распределения CB X – числа станков, которым потребуется наладка в течение смены, если n = 4; 2) оценить вероятность того, что за смену потребуют наладки 20 станков, если n = 100. Наладка потребуется станкам из п= 4 представляет случайную величину Хсмножеством значений X= т =0, 1, 2, 3, 4, вероятности которых определяются по формуле Бернулли: В нашем случае n = 4, p = 0,3, q = 1-p = 0,7 Вычислим Р(Х=0)= 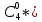 0,30*0,74=1*1*0,2401=0,2401 0,30*0,74=1*1*0,2401=0,2401Р(Х=1)= 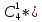 0,31*0,73=4*0,3*0,343=0,4116 0,31*0,73=4*0,3*0,343=0,4116Р(Х=2)= 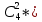 0,32*0,72=6*0,09*0,49=0,2646 0,32*0,72=6*0,09*0,49=0,2646Р(Х=3)= 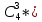 0,33*0,71=4*0,027*0,7=0,0756 0,33*0,71=4*0,027*0,7=0,0756 Р(Х=4)= 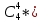 0,34*0,70=1*0,0081*1=0,0081 0,34*0,70=1*0,0081*1=0,0081(Здесь учтено, что Ряд распределения имеет вид
проверка Р=0,2401+0,4116+0,2646+0,0756+0,0081=1 к=20 n=100 p=0.3 q=1-0.3=0.7 2) 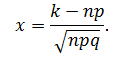 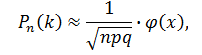 х= 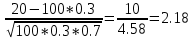 (2.18)=0.485 P(20)= 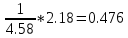 Задача 3. Непрерывная CB X задана функцией распределения 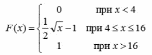 Найти: 1) плотность распределения f(x); 2) M(X) и D(X); 3) P(3 < X < 9); 4) вероятность того, что в 4 независимых испытаниях CB X ровно 2 раза примет значения, принадлежащие интервалу (3; 9). Случайная величина Х задана функцией распределения F(x): 0, x 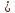 4 4 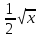 -1≤ x ≤ 16 -1≤ x ≤ 16 1, x > 16 Найдем плотность распределения f(x), как производную от функции распределения F(x): Плотность распределения f(x): 0, x < 4 0, x ≥ 16 Математическое ожидание. Дисперсия. = 1/10•165/2 - (1/10•45/2) - (28/3)2 = 544/45 Среднеквадратическое отклонение. Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a P(0.25< X <0.75) = F(0.75)-F(0.25) = 0.5 Р(3 Вероятность того, что Х примет значение xЄ(3; 9) ровно 2 раза в 4-х испытаниях, равна по ф-ле Бернулли: q=1-0.24=0.76 Р4 (2) = 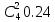 2*0.762=6*0.0576*0.5776=0.2 2*0.762=6*0.0576*0.5776=0.2Задача 4. Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Случайная величина X – разница между временем, показываемым на табло и истинным временем имеет равномерное распределение. Найти вероятность того, что в некоторый момент времени часы укажут время, которое отличается от истинного: а) не менее, чем на 10 с и не более, чем на 25 с; б) не менее, чем на 25 с. а)М(Х)=(10+25)/2=17,5 =(25-10)/2 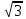 =4,3 =4,3Ф( 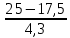 )-Ф( )-Ф(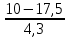 )=Ф(1,7)-Ф(-1,7)=0,46+0,46=0,92 )=Ф(1,7)-Ф(-1,7)=0,46+0,46=0,92б)Показание часов в данное мгновение времени можно рассматривать как случайную непрерывную величину X, которая равномерно распределена на интервале (0;60). Плотность распределения этой случайной величины равно:
Пусть событие А — «в данное мгновение часы покажут время, которое отличается от истинного не более чем на 25 с». Данное событие может произойти или в интервале (0;25), или в интервале (35;60). Так как эти интервалы не пересекаются, то по теореме сложения вероятностей двух независимых событий имеем: Р(А)=Р(0
|
