Задачи. Решение Текущая стоимость акции Где номинальная цена акции размере дивиденда годовых от номинала
 Скачать 108.14 Kb. Скачать 108.14 Kb.
|
|
Задача 1. Инвестор приобрел акцию по номинальной цене 1000 руб. при размере дивиденда 10% годовых от номинала, которые будут выплачиваться в будущем. Учетная ставка банковского процента - 8% годовых. Определите текущую стоимость акции. Решение: Текущая стоимость акции 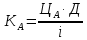 Где 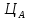 - номинальная цена акции - номинальная цена акции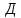 - размере дивиденда годовых от номинала - размере дивиденда годовых от номинала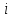 - учетная ставка банковского процента - учетная ставка банковского процента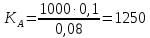 руб. руб.Ответ: Текущая стоимость акции 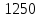 руб. руб.Задача 2. Компания в настоящее время выплачивает дивиденды в размере 4руб. за акцию. Ожидается, что дивиденды будут расти на 3% в год. Ставка дисконтирования равна 10%. Какова внутренняя стоимость акций данной компании? На рынке акции компании продаются по цене 110руб. за акцию. Какова внутренняя норма доходности акции (IRR)? Стоит ли продавать акции? Решение: Для решения данной задачи можно воспользоваться моделью дисконтирования дивидендов (DDM). По условию задачи 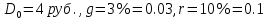 Рассчитаем внутреннюю стоимость акции по модель Гордона, поскольку темп прироста дивидендов не меняется: 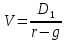 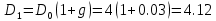 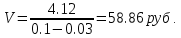 Таким образом, внутренняя стоимость акции составит 58,86 руб. Чистый приведенный доход по акции, где Р- текущая рыночная цена 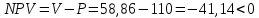 Следовательно акция переоценена рынком на 41,14руб. 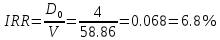 Так как внутренняя стоимость акции (58,86руб.) меньше рыночной (110 руб.), то имеет смысл продать акции. Ответ: внутренняя стоимость акций данной компании равна 58,86руб., внутренняя норма доходности акции (IRR)равна 6,8%. Акции стоит продавать. Задача 3. Гражданин владеет облигацией, номинал которой составляет 1000 рублей, а срок до погашения- 3года. Ежегодные процентные платежи по ней составляют 75 рублей, первый будет сделан через год. Текущий курс этой облигации составляет 975,48рублей. Приемлемая норма прибыли составляет 10%. Стоит ли гражданину держать эту облигацию или продать? Решение: По условию задачи 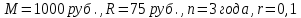 . .Для определения внутренней стоимости такой облигации необходимо определить современную стоимость купонного дохода и номинала бумаги. В случае, если выплата купонного дохода будет производиться раз в год, то расчет стоимости выглядит так: Vо=Рк+Рd где Vо – внутренняя стоимость облигации, руб., Рк – современная стоимость купонного дохода, руб., Рd – современная стоимость номинала облигации, руб. 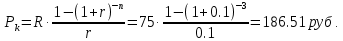 Затем рассчитаем Рd: 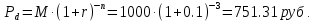 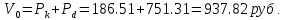 . Текущий курс этой облигации 975,48 рублей превышает Vо= 937,82 руб., следовательно, облигацию можно продать. Ответ: Облигацию стоит продать Задача 4. АО выпустило облигации без выплаты процентов сроком на пять лет. Текущий курс облигации- 72. Определите доходность облигации. Решение: 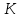 - текущий курс облигации- 72 - текущий курс облигации- 72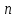 - срок- 5лет - срок- 5летДля бескупонной облигации (без выплаты процентов) полная доходность 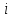 будет исчисляться по формуле: будет исчисляться по формуле: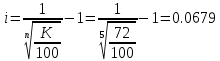 т.е. облигация обеспечивает 6.79% годового дохода. Ответ: доходность облигации-6,79% годовых Задача 5. Облигации реализована по курсу 89 сроком на пять лет, начисление процентов производится по ставке 15% годовых, при условии, что проценты и номинал погашаются в конце срока. Определите доходность облигации. Решение: 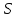 - ставка начисления процентов, 20%=0,2 - ставка начисления процентов, 20%=0,2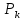 - курс реализации облигации =89 - курс реализации облигации =89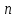 - срок- 5лет - срок- 5летДоходность облигации рассчитывается по формуле 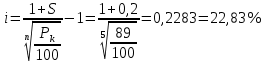 Ответ: доходность облигации- 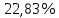 |
