математика. Решение 1) Двумя предметами увлекаются человек (из условия)
 Скачать 76.83 Kb. Скачать 76.83 Kb.
|
|
1. В группе 38 человек. Из них 16 увлекаются математикой, 17 – физикой, 18 – историей. Увлекаются двумя предметами – математикой и физикой – четверо, математикой и историей – трое, физикой и историей – пятеро. Трое не увлекаются ни математикой, ни физикой, ни историей. Сколько человек увлекается тремя предметами? Решение: 1) Двумя предметами увлекаются  человек (из условия) человек (из условия)2) Пусть 3-мя предметами увлекаются х человек. Предметы для облегчения Физика, Математика, История. Тогда только Математикой увлекаются:  чел. (т.е. исключили Физика+Математика, История+Математика, Физика+История+Математика). чел. (т.е. исключили Физика+Математика, История+Математика, Физика+История+Математика).Только физикой увлекаются: 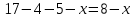 чел. (исключили Математика+Физика, История+Физика, Математика+История+Физика) чел. (исключили Математика+Физика, История+Физика, Математика+История+Физика)Только историей увлекаются:  чел. (исключили Физика+История, Математика+История, Физика+Математика+История) чел. (исключили Физика+История, Математика+История, Физика+Математика+История)Всего занимаются: а) только одним предметом 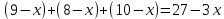 б) только двумя предметами 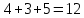 в) только тремя предметами 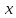 Всего занимается 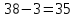 человек. человек.Просуммируем а), б), в) и решим уравнение 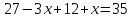 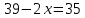 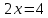 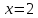 – человека занимаются всеми тремя предметами – человека занимаются всеми тремя предметами2. Решите систему линейных уравнений по формулам Крамера, методом Гаусса, методами матричного исчисления, представив систему в матричном виде: 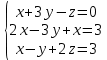 Решение: 1) 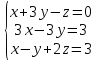 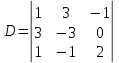 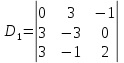 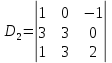 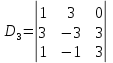  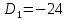 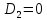 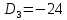 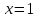 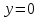 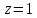 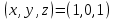 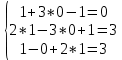 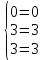  2) 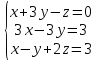 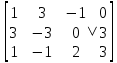 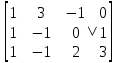 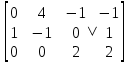 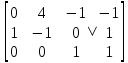 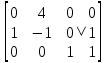 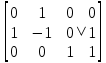 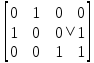 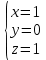 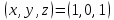 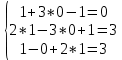 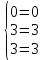 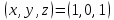 3. Найдите приближенное значение 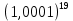 Решение: 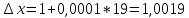 4. Найдите неопределенные интегралы, правильность найденных интегралов проверьте дифференцированием: 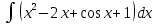 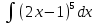 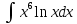 Решение: 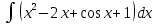 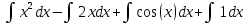 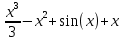 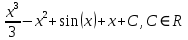 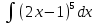 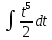 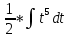  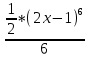 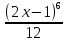 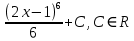 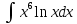   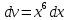  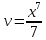 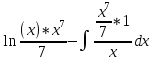 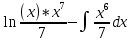   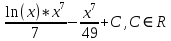 5. Найдите объем тела, полученного вращением вокруг оси 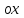 криволинейной трапеции, ограниченной кривой криволинейной трапеции, ограниченной кривой 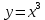 , осью , осью 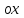 и прямыми и прямыми 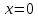 , , 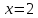 Решение: 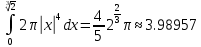  6. Найдите сумму, разность, произведение и частное комплексных чисел 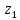 и и  , если , если 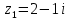 , , 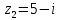 . .Решение: 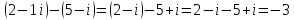 ( 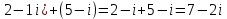 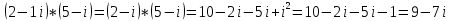 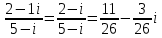 7. Решите дифференциальные уравнения с разделяющимися переменными: 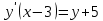 Решение:  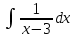 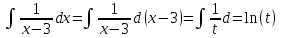 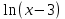 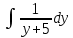 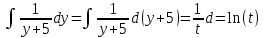  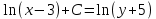 8. Решите однородное дифференциальное уравнение с постоянными коэффициентами:  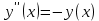   9. Исследуйте ряд на сходимость: 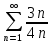 Решение: 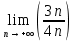  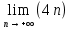 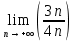 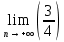 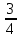 Расходится. 10. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго. Какова вероятность того, что взятая наугад деталь бракованная? Решение: Возьмем с конвейера наудачу одну деталь и рассмотрим событие 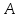 – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: 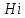 – взятая наудачу деталь обработана на i-ом станке, – взятая наудачу деталь обработана на i-ом станке, 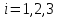 . .Условные вероятности (в условии задачи они даны в форме процентов): 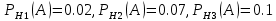 Зависимости между производительностями станков означают: 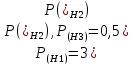 . .Для того, чтобы вероятности появления гипотез, придется решить эти уравнения. 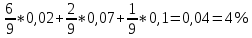 |
