Математика высшая. Контрольная работа Марина. Решение расстояние между точками находят по формуле 1 2 уравнение прямой, проходящей через две точки
 Скачать 62.36 Kb. Скачать 62.36 Kb.
|
|
Контрольная работа 1. 1  6. Даны координаты вершин треугольника АВС: А(-2;11), В(10;2), С(8;16). 6. Даны координаты вершин треугольника АВС: А(-2;11), В(10;2), С(8;16). Вычислить: 1) длину стороны АВ; записать уравнения: 2) стороны АВ; 3) высоты CD, опущенной из вершины С на сторону АВ; 4) медианы АЕ; 5) окружности для которой медиана АЕ служит диаметром. Дано: А(-2;11), В(10;2), С(8;16) Найти: 1) 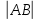 2) уравнение АВ 3) уравнение CD, CD⊥АВ 2) уравнение АВ 3) уравнение CD, CD⊥АВ4) уравнение АЕ, где ВЕ=ЕС 5) уравнение окружности, где АЕ=d Решение: расстояние между точками находят по формуле: 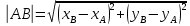 1)  2) уравнение прямой, проходящей через две точки:  Подставляя координаты точек А и В, получим уравнение прямой АВ:  12(y-11)=-9(x+2) 12y-132=-9x-18 9x+12y-132+18=0 9+12y-114=0 |:3 3x+4y-38=0 уравнение прямой (AB) Решим это уравнение относительно у, находим уравнение прямой стороны АВ в виде уравнения прямой с угловым коэффициентом 4y=-3x+38 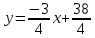 (AB), (AB), 3) Высота СД перпендикулярна стороне АВ. Чтобы найти угловой коэффициент высоты СД, воспользуемся условием перпендикулярности прямых. kCD=  Подставим координаты точки С и найденного углового коэффициента высоты в формулу:  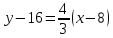  3y-48=4x-32 3y-4x-48+32=0 -4x+3y-16=0 (CD) 4) Чтобы найти уравнение медианы АЕ, определим координаты точки Е, которая является серединой стороны ВС, применяя формулу деления отрезка на две равные части: 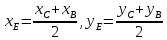   E(9;9) E(9;9)Подставим координаты точекA(-2;11) E(9;9) в формулу:    -2(x+2)=11(y-11) -2x-4-11y+121=0 -2x-11y+117=0 (AE) 5) уравнение окружности радиуса Rс центром в точке Q(a;b) имеет вид:  Применяя формулу 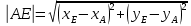 находим длину стороны АЕ \AE\=  R=  Так как медиана (АЕ) является диаметром искомой окружности, то ее центр Q есть середина отрезка АЕ. Применяем формулу деления отрезка пополам:   (x-3,5)2+(y-10)2=  (x-3,5)2+(y-10)2=125 36. Даны координаты вершин пирамиды ABCD: А(-3;-6;2), В(1;-2;0), С(-1;5;-8), D(-3;-4;3). Требуется: 1) записать векторы  в системе орт и вычислить модули этих векторов; 2) определить угол между векторами в системе орт и вычислить модули этих векторов; 2) определить угол между векторами  ; 3) определить проекцию вектора ; 3) определить проекцию вектора  на вектор на вектор 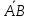 ; 4) вычислить площадь грани АВС; 5) вычислить объем пирамиды ABCD. ; 4) вычислить площадь грани АВС; 5) вычислить объем пирамиды ABCD.Дано: ABCD – пирамида А(-3;-6;2), В(1;-2;0), С(-1;5;-8), D(-3;-4;3) Найти: 1)  2) 2)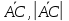 3) 3) 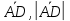 4) 4)  5)  6) 6)  6) Vпир 6) VпирРешение: Если даны точки 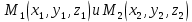 , то проекция вектора на координатные оси находятся по формулам: , то проекция вектора на координатные оси находятся по формулам: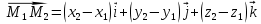 длина вектора вычисляется по формуле:     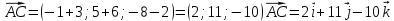   Косинус угла между двумя векторами равен скалярному произведению этих векторов, деленному на произведение их модулей. Скалярное произведение векторов находим по формуле:  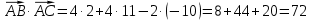 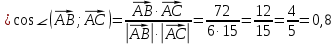   Проекция вектора Проекция вектора на вектор на вектор равна скалярному произведению этих векторов, деленному на модуль вектора равна скалярному произведению этих векторов, деленному на модуль вектора   Площадь грани АВС равна половине площади параллелограмма, построенного на векторах  . Площадь параллелограмма, построенного на векторах . Площадь параллелограмма, построенного на векторах  произведения векторов произведения векторов  и и 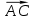 . Векторное произведение вычислим по формуле: . Векторное произведение вычислим по формуле:   = =    Объем параллелепипеда, построенного на трех некомпланарных векторах, равен абсолютной величине их смешанного произведения. Смешанное произведение векторов находят по формуле:     Vпарал=\108\=108 (куб.ед)  56. Решите систему трех уравнений с тремя неизвестными при помощи определителей по формулам Крамера.  Решение:  вычислим определитель вычислим определитель  , составленный из коэффициентов при неизвестных и применяя правило треугольников. , составленный из коэффициентов при неизвестных и применяя правило треугольников. 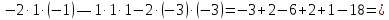  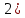 вычислим определитель вычислим определитель  , полученный из , полученный из  заменой первого столбца столбцом свободных коэффициентов и применяя правило треугольников. заменой первого столбца столбцом свободных коэффициентов и применяя правило треугольников.   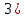 вычислим определитель вычислим определитель  , полученный из , полученный из  заменой второго столбца столбцом свободных коэффициентов и применяя правило треугольников заменой второго столбца столбцом свободных коэффициентов и применяя правило треугольников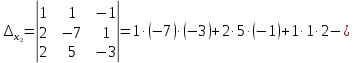    вычислим определитель вычислим определитель 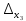 , полученный из , полученный из  заменой третьего столбца столбцом свободных коэффициентов и применяя правило треугольников заменой третьего столбца столбцом свободных коэффициентов и применяя правило треугольников   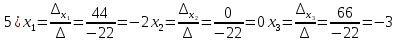 Ответ: (-2;0;-3) 76. Вычислите указанные пределы   Непосредственная подстановка предельного значения аргумента приводит к неопределенности вида Непосредственная подстановка предельного значения аргумента приводит к неопределенности вида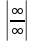 . Чтобы раскрыть эту неопределенность, разделим числитель и знаменатель на х3. . Чтобы раскрыть эту неопределенность, разделим числитель и знаменатель на х3.   )Непосредственная подстановка предельного значения аргумента х=10 приводит к неопределенности вида )Непосредственная подстановка предельного значения аргумента х=10 приводит к неопределенности вида , чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и сократим члены дроби на общий множитель (х-10) , чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и сократим члены дроби на общий множитель (х-10)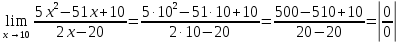 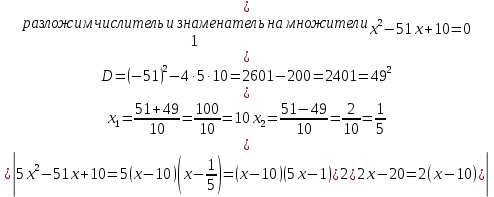  96. Определите производные и дифференциалы указанных функций:  Решение: Используем правила дифференцирования и таблицу:     Решение: последовательно применяя правила производной произведения и таблицу:    Решение: Используем правила дифференцирования частного и сложной функции, получаем:  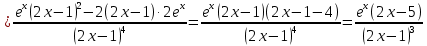  Решение: Воспользуемся правила дифференцирования сложной функции: 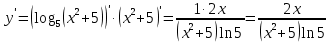 116. Исследуйте данную функцию на экстремум и постройте ее график. Исследование предусматривает определение точек экстремума, интервалов возрастания и убывания функции, точек пересечения интервалов выпуклости и вогнутости графика функции.  1.Функция целая (нет деления на переменную) ⇒ область определения множество действительных чисел.   функция не является ни четной, ни нечетной, т.к. y(-x)≠y(x), y(-x)≠-y(x)  (вычислим производную и найдем критические точки-точки в которых производная обращается в ноль) (вычислим производную и найдем критические точки-точки в которых производная обращается в ноль)  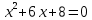    возрастает y’>0 (-∞;-4) ∪(-2;+∞) убывает y’<0 (-4;-2) 4.Найдем точки экстремума(в условие подставим критические точки) y(-4)=(-4)3+9(-4)2+24(-4)+17=-64+144-96+17=-160+161=1 (-4;1) – max y(-2)=(-2)3+9(-2)2+24(-2)+17=-8+36-48+17=-56+53=-3 (-2;-3) – min 5.Вычислим вторую производную и определим точки перегиба y’’=(3x2)’+(18x)’+(24)’=6x+18 6  x+18=0 x+18=06x=- 18 x=-18:6=-3 y(-3)=(-3)3+9(-3)2+24(-3)+17=-27+81-72+17=-99+98=-1 (-3;-1) – точка перегиба y’’<0 (-∞;-3) y’’>0 (-3;+∞) 6. функция целая – асимптот нет
ax3+bx2+cx+d=0 теорема Виета-Кардана     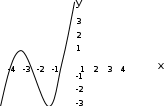 136. Найти неопределенные интегралы:  Решение: используем свойства и таблицу интегралов:  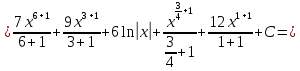 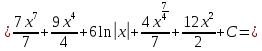 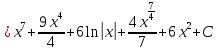 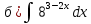 Решение: применяем метод замены переменной и таблицу интегралов:    Решение: применяем метод замены переменной и таблицу интегралов: 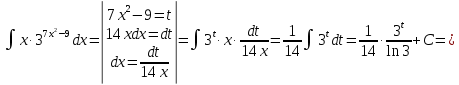   Решение: применяем метод интегрирования по частям:  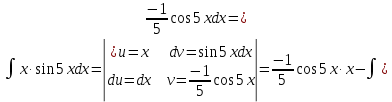  156. Даны уравнения параболы и прямой. Вычислить с помощью определенного интеграла площадь фигуры, ограниченной данными линиями; сделать чертеж и заштриховать искомую область. Решение: построим фигуру, ограниченную указанными линиями. 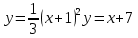
 Найдем пределы интегрирования    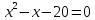 D=1+80=81 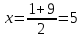  Вычислим площадь 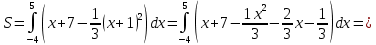    176. Для заданной функции z=f(x;y) доказать справедливость указанного равенства.  Решение: вычислим частные производные 1-ого порядка и 2-го порядка, смешанные производные для функции z. 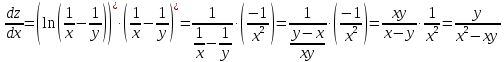    Подставим найденные производные в условие и преобразуем левую часть.       Что и требовалось доказать. |


