Контрольная работа по математике (2 семестр)
1. Вычислить неопределенные интегралы
1.1
|
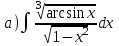
|
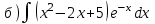
|
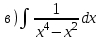
|
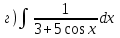
|
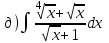
|
1.2
|
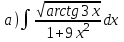
|
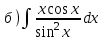
|

|
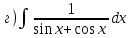
|
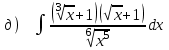
|
1.3
|
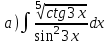
|
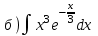
|
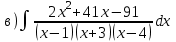
|
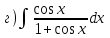
|
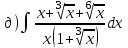
|
1.4
|
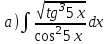
|
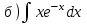
|
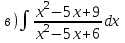
|
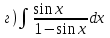
|
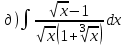
|
1.5
|
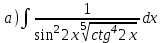
|
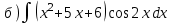
|
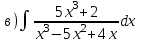
|
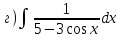
|
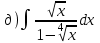
|
1.6
|
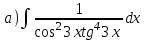
|
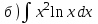
|
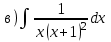
|
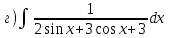
|
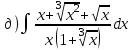
|
1.7
|
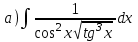
|
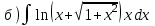
|
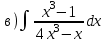
|
|
|
1.8
|
|
|
|
|
|
1.9
|
|
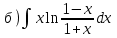
|
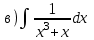
|
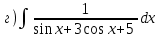
|
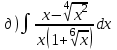
|
1.10
|
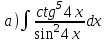
|
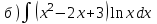
|
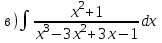
|
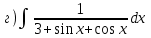
|
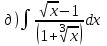
|
2. С помощью определенного интеграла вычислить площадь плоской фигуры, ограниченной линиями
2.1
|
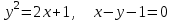
|
2.2
|

|
2.3
|
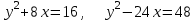
|
2.4
|
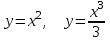
|
2.5
|

|
2.6
|
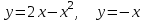
|
2.7
|
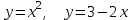
|
2.8
|
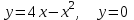
|
2.9
|
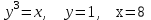
|
2.10
|
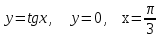
|
3. С помощью определенного интеграла вычислить длину дуги кривой между указанными точками
3.1
|
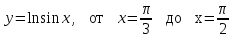
|
3.2
|
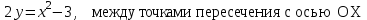
|
3.3
|
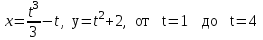
|
3.4
|
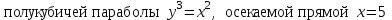
|
3.5
|
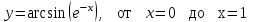
|
3.6
|
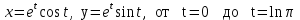
|
3.7
|
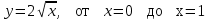
|
3.8
|
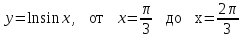
|
3.9
|
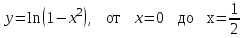
|
3.10
|
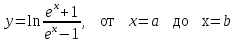
|
4. С помощью определенного интеграла вычислить объем тела, полученного вращением фигуры Ф вокруг указанной оси координат
4.1
|
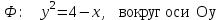
|
4.2
|
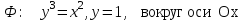
|
4.3
|
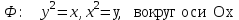
|
4.4
|
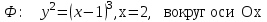
|
4.5
|
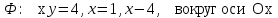
|
4.6
|
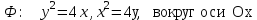
|
4.7
|
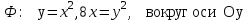
|
4.8
|
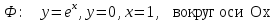
|
4.9
|
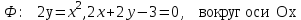
|
4.10
|
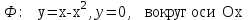
|
5. Вычислить несобственный интеграл или доказать его расходимость
5.1
|
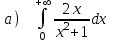
|
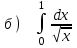
|
5.2
|
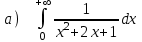
|
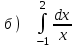
|
5.3
|
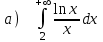
|
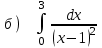
|
5.4
|
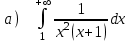
|
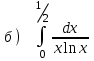
|
5.5
|
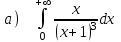
|
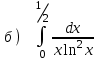
|
5.6
|
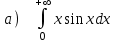
|
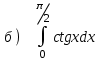
|
5.7
|
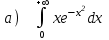
|
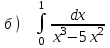
|
5.8
|
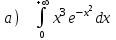
|
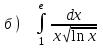
|
5.9
|
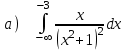
|
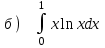
|
5.10
|
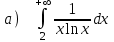
|
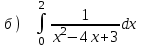
|
6. Найти решения дифференциальных уравнений первого порядка
6.1
|
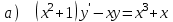
|
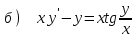
|
6.2
|
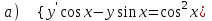
|
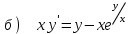
|
6.3
|
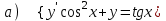
|
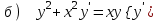
|
6.4
|
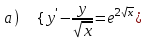
|
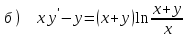
|
6.5
|
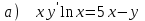
|
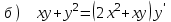
|
6.6
|
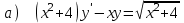
|
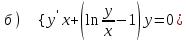
|
6.7
|
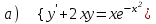
|
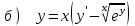
|
6.8
|
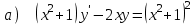
|
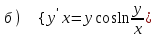
|
6.9
|
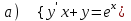
|
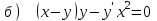
|
6.10
|
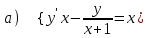
|
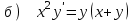
|
7. Найти решения дифференциальных уравнений высших порядков
7.1
|
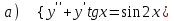
|
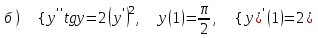
|
7.2
|
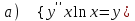
|
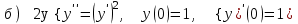
|
7.3
|
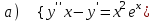
|
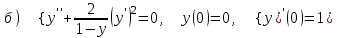
|
7.4
|
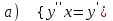
|
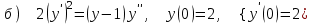
|
7.5
|
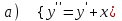
|
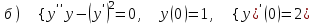
|
7.6
|
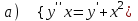
|
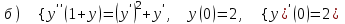
|
7.7
|
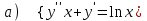
|
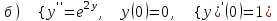
|
7.8
|
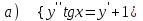
|
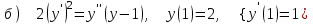
|
7.9
|
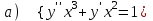
|
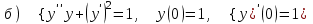
|
7.10
|
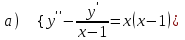
|
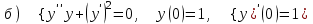
|
8. Найти решения линейного неоднородного дифференциального уравнения второго порядка
8.1
|
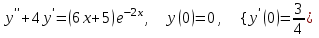
|
8.2
|
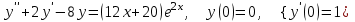
|
8.3
|
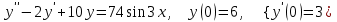
|
8.4
|
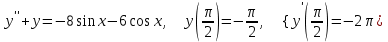
|
8.5
|
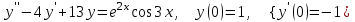
|
8.6
|
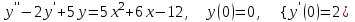
|
8.7
|
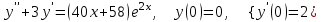
|
8.8
|
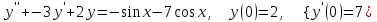
|
8.9
|
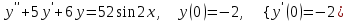
|
8.10
|
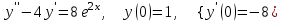
|
9. Решить систему дифференциальных уравнений
9.1
|
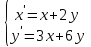
|
9.2
|
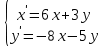
|
9.3
|
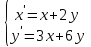
|
9.4
|
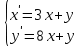
|
9.5
|
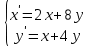
|
9.6
|
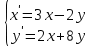
|
9.7
|
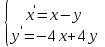
|
9.8
|
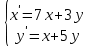
|
9.9
|
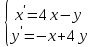
|
9.10
|
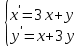
|
10. Составить дифференциальное уравнение, удовлетворяющее заданным условиям, и найти его решение
10.1
|
Найти кривую, проходящую через точку А(1,4), для которой отрезок касательной между точкой касания и осью абсцисс делится пополам в тоске пересечения с осью ординат.
|
10.2
|
Кривая проходит через точку 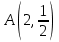 . В произвольной точке этой кривой проведена касательная, точка пересечения которой с осью ОХ имеет абсциссу вдвое большую, чем абсцисса точки касания. Найти кривую. . В произвольной точке этой кривой проведена касательная, точка пересечения которой с осью ОХ имеет абсциссу вдвое большую, чем абсцисса точки касания. Найти кривую.
|
10.3
|
Найти кривую, проходящую через точку А(0,-2), для которой угловой коэффициент касательной в любой ее точке равен ординате этой точки, увеличенной на 3.
|
10.4
|
Найти кривую, проходящую через точку А(1,1), если известно, что произведение абсциссы любой точки кривой на угловой коэффициент касательной к кривой в этой точке равно удвоенной сумме координат точки.
|
10.5
|
Найти кривую, проходящую через точку А(0,1), и обладающую следующим свойством: треугольник, образованный осью ОУ, касательной к кривой в произвольной ее точке и радиус-вектором точки касания, равнобедренный, причем его основанием служит отрезок касательной от точки касания до оси ординат.
|
10.6
|
Найти кривую, проходящую через точку А(4,2), у которой отрезок, отсекаемый касательной на оси ординат, равен полусумме координат точки касания.
|
10.7
|
Найти кривую, проходящую через точку А(1,-1), для которой отрезок, отсекаемый касательной на оси ординат, равен квадрату абсциссы точки касания.
|
10.8
|
Найти линию, проходящую через точку 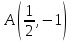 , если длина отрезка полуоси абсцисс, отсекаемого ее касательной, равна квадрату абсциссы точки касания. , если длина отрезка полуоси абсцисс, отсекаемого ее касательной, равна квадрату абсциссы точки касания.
|
10.9
|
Найти линию, проходящую через точку А(2,3) и обладающую тем свойством, что отрезок любой ее касательной, заключенный между осями, делится пополам в точке касания.
|
10.10
|
Найти кривую, проходящую через точку А(1,-1) и обладающую следующим свойством: длина отрезка, отсекаемого на оси ординат любой касательной, равна утроенной абсциссе точки касания.
| |
 Скачать 241.57 Kb.
Скачать 241.57 Kb.
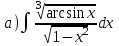


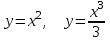

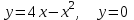
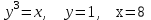
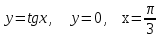
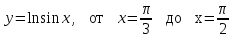
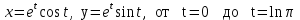
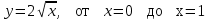
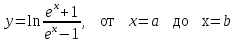
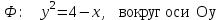
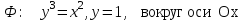
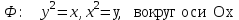
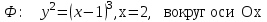
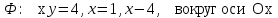
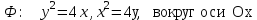
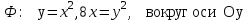
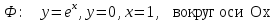
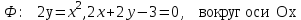
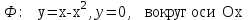
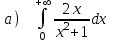
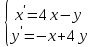
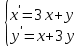
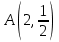 . В произвольной точке этой кривой проведена касательная, точка пересечения которой с осью ОХ имеет абсциссу вдвое большую, чем абсцисса точки касания. Найти кривую.
. В произвольной точке этой кривой проведена касательная, точка пересечения которой с осью ОХ имеет абсциссу вдвое большую, чем абсцисса точки касания. Найти кривую.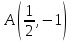 , если длина отрезка полуоси абсцисс, отсекаемого ее касательной, равна квадрату абсциссы точки касания.
, если длина отрезка полуоси абсцисс, отсекаемого ее касательной, равна квадрату абсциссы точки касания.