Решение непрерывна при Тогда несобственный интеграл Вычислим неопределенный интеграл
 Скачать 234.96 Kb.
|
|
Задача 1. Вычислить несобственный интеграл или доказать его расходимость:  Решение:  непрерывна при  Тогда несобственный интеграл:  Вычислим неопределенный интеграл: 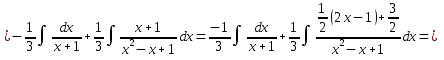 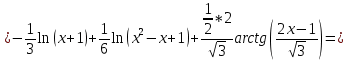 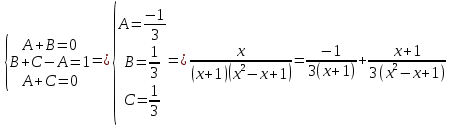 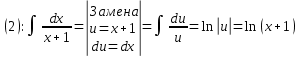 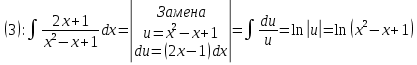 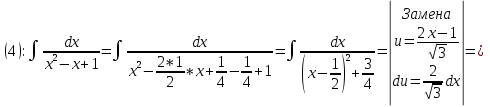 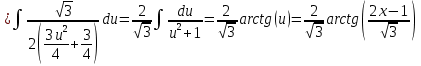     Вычислим несобственный интеграл с помощью вышеприведенной формулы:    Задача 2. Вычислить несобственный интеграл или доказать его расходимость:  Решение:  в точке x=7 терпит бесконечный разрыв.Вычислим неопределенный интеграл: 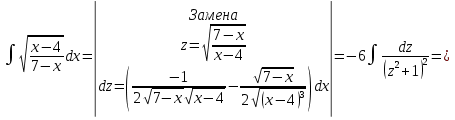 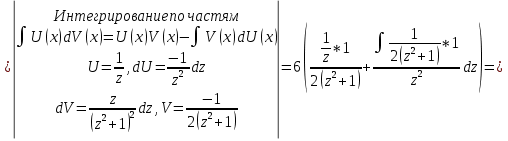 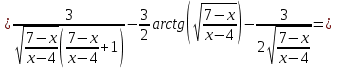   Вычислим несобственный интеграл: 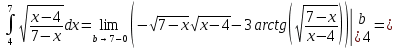 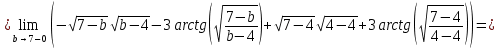  Задача 3. Исследовать на сходимость несобственный интеграл  Решение: Подынтегральная функция  непрерывна для любого x [2;+)Воспользуемся теоремой: Если для любого xA (Aa) выполнено равенство |f(x)||g(x)|, тогда если интеграл  абсолютно сходится, то интеграл  также абсолютно сходится, а если абсолютно расходится, то также расходится.Рассмотрим функции 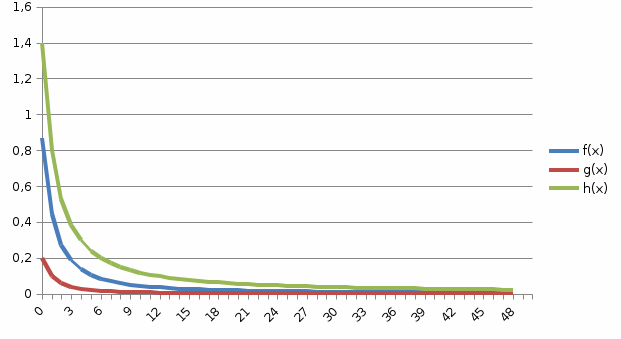 . Для любого x [2;+) справедливо  что наглядно видно на графике.  Исследуем сходимость интегралов 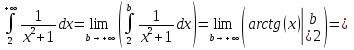   Следовательно 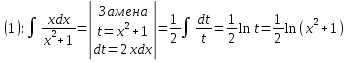 сходится.    Следовательно  расходится, следовательно, расходится исходный интеграл  Задача 4. Исследовать на сходимость несобственный интеграл 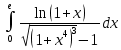 Решение: Подынтегральная функция  в точке x=0 терпит разрыв.Воспользуемся теоремой: Если для любого x[b-;b) выполнено неравенство 0f(x)g(x), тогда если интеграл  сходится, то  также сходится; а если расходится, то также расходится.Рассмотрим 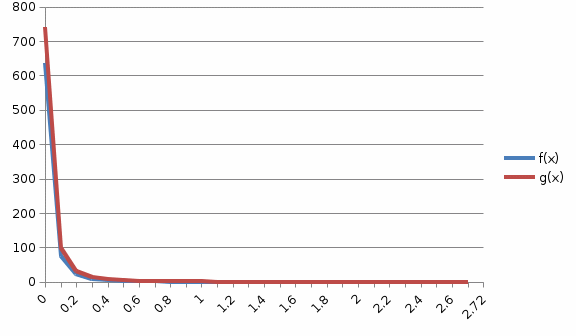 . Для любого x (0;e] справедливо   Исследуем сходимость интеграла 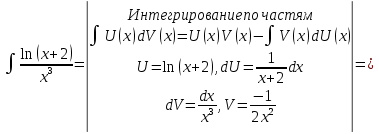      .    Следовательно, интеграл 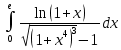сходится, а значит, сходится и исходный интеграл Задача 5. Вычислить площадь фигуры, ограниченной линиями  Решение: Изобразим графически фигуру, площадь которой предлагается найти: 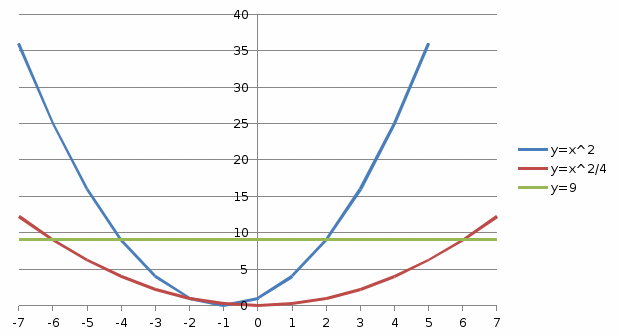 На графике видно, что фигура, ограниченная данными графиками (окрашена синим) состоит из двух симметрично расположенных частей. Следовательно, необходимо найти площадь одной из них и, умножив на 2, получим площадь искомой фигуры. Если на отрезке [a,b] некоторая непрерывная функция f(x) больше либо равна некоторой непрерывной функции g(x), то площадь фигуры, ограниченной графиками данных функций и прямыми x=a, x=b, можно найти по формуле:  Для того чтобы найти пределы интегрирования, найдем точки пересечения парабол и прямой: 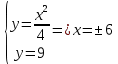  Воспользуемся вышеприведенной формулой:   Тогда площадь искомой фигуры: 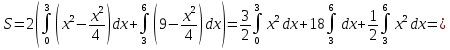  Задача 6. Вычислить площадь фигуры, ограниченной линиями  Решение: Схематически фигура, площадь которой требуется найти, выглядит следующим образом: 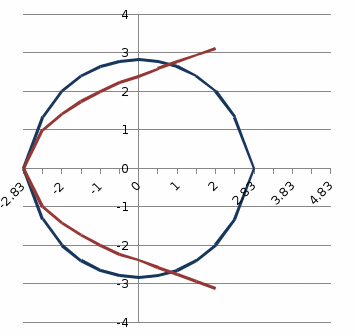 В данном случае удобнее рассматривать данную фигуру как симметричную относительно оси ОХ и интегрировать по y. Найдем пределы интегрирования: 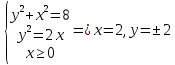 Если на отрезке [a,b] некоторая непрерывная функция f(x) больше либо равна некоторой непрерывной функции g(x), то площадь фигуры, ограниченной графиками данных функций и прямыми x=a, x=b, можно найти по формуле: В нашем случае  Тогда площадь искомой фигуры:         Задача 7. Вычислить площади фигур, ограниченных графиками функций  Решение: Изобразим графически фигуру, площадь которой требуется найти:   На графике очевидно, что пределы интегрирования по x [0;1]   Задача 8. Вычислить площадь фигуры, ограниченной линиями:  Решение: Кривая, заданная параметрически уравнением  - астроида. Поскольку задано условие  построим правую половину астроиды и найдем площадь фигуры, лежащей правее прямой x=1. Так как фигура симметрична относительно оси абсцисс, поэтому вычислим верхнюю половину площади и удвоим результат.  Площадь фигуры, заданной параметрически:  Найдем значения параметра, которые определяют точки пересечения прямой x=1 и астроиды:    Правой вершине астроиды соответствует значение t=0  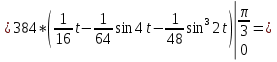 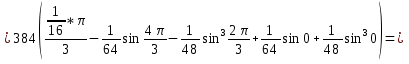 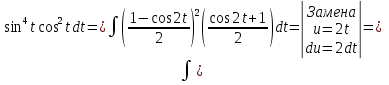 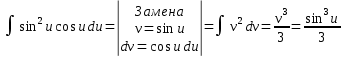      Задача 9. Вычислить площади фигур, ограниченных линиями, заданными уравнениями.  Решение: Построим заданный эллипс. В качестве переменной интегрирования для поиска площади фигуры, удобнее использовать y. Поскольку фигура симметрична относительно оси OY, найдем площадь половины, затем удвоим.   Площадь фигуры, заданной параметрически:   Найдем значения параметра, которые определяют точки пересечения прямой y=2 и эллипса:       Задача 10. Вычислить площадь фигуры, ограниченной линиями  Решение: Заданные уравнения в полярной системе координат описывают окружности. Для наглядности построим график:  Необходимо найти площадь кольца, для этого нужно из площади большего круга  вычесть площадь меньшего круга  Площадь фигуры, заданной в полярной системе координат, вычисляется по формуле:  Вычислим площадь большего круга:   Вычислим площадь меньшего круга:   Тогда площадь искомой фигуры:  Задача 11. Вычислить площади фигур, ограниченных линиями, заданными в полярных координатах.  Решение: Заданное уравнение описывает в полярной системе координат окружность со смещенным центром, таким образом, необходимо найти площадь круга. Площадь фигуры, заданной в полярной системе координат, вычисляется по формуле:         Задача 12. Вычислить длину дуги кривой  Решение: Длина кривой, график которой задан непрерывной функцией y= f(x) рассчитывается по следующей формуле:  В данном случае       Задача 13. Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат  Решение: Длина кривой, график которой задан непрерывной функцией y= f(x) рассчитывается по следующей формуле: 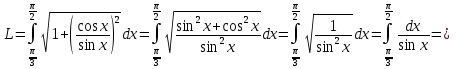 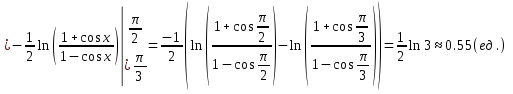 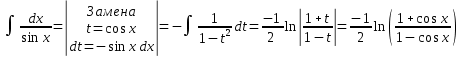  Задача 14. Вычислить длину дуги кривой  Решение: Если линия задана параметрическими уравнениями x=x(t), y=y(t), то длина дуги кривой, которая прочерчивается при изменении параметра t в пределах [t1,t2] , рассчитывается по формуле: 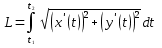 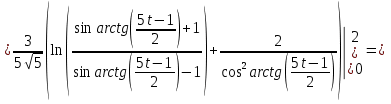  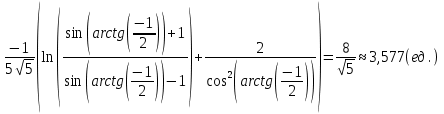 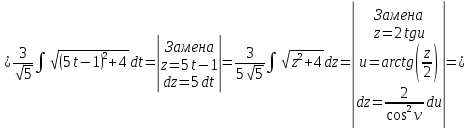 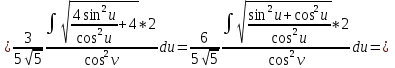            Задача 15. Вычислить длины дуг кривых, заданных параметрическими уравнениями  Решение: Если линия задана параметрическими уравнениями x=x(t), y=y(t), то длина дуги кривой, которая прочерчивается при изменении параметра t в пределах [t1,t2] , рассчитывается по формуле:        Задача 16. Вычислить длину дуги кривой  находящейся внутри окружности r = 5Решение: Если кривая задана в полярных координатах уравнением r=r(), где , при этом на промежутке [;] функция имеет непрерывную производную r’(), то длина дуги кривой выражается следующей формулой:  Поскольку требуется найти часть логарифмической спирали, лежащей внутри окружности r = 5, пределы интегрирования [0;2].    Задача 17. Вычислить длины дуг кривых, заданных уравнениями в полярных координатах.  Решение: Если кривая задана в полярных координатах уравнением r=r(), где , при этом на промежутке [;] функция имеет непрерывную производную r’(), то длина дуги кривой выражается следующей формулой:  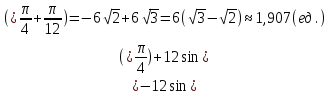 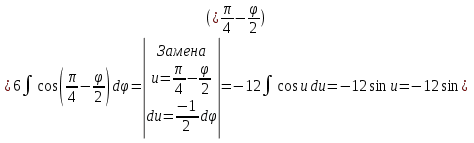     Задача 18. Найти объем тела, полученного вращением фигуры, ограниченной графиками функций вокруг оси OX  Решение: Изобразим схематически график функции y=f(x). Фигура, которая вращается вокруг оси ОХ, изображена на рисунке синим цветом. 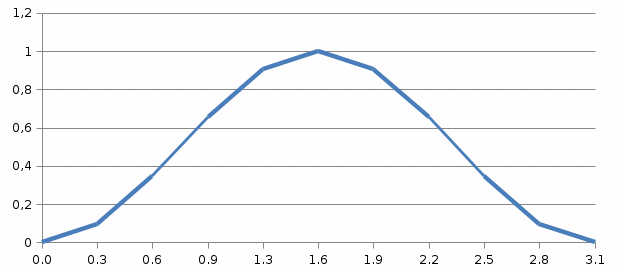 Объем тела вращения можно вычислить по формуле:       Задача19. Найти объем тела, полученного вращением фигуры, ограниченной графиками функций вокруг оси OY  Решение: Составим чертеж. Фигура, которая вращается вокруг оси OY, окрашена синим цветом. Очевидно, что объем данной фигуры состоит из двух симметричных частей. Разделим фигуру на две части (красная пунктирная линия y=1). При y[0;1] объем тела вращения можно найти как разность объемов двух усеченных конусов: большего – V1  и меньшего – V2  На отрезке от 1 до 2 объем тела вращения можно найти как разницу объемов тел вращения ветки гиперболы V3  и усеченного конуса V4  Объем тела вращения в общем случае вычисляется по формуле: 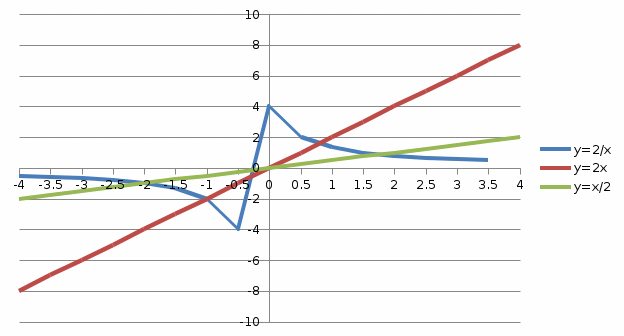  Из чертежа видно, что пределы интегрирования по оси OY [0;2]     Задача 20. Вычислить объемы тел, образованных вращением фигур, ограниченных графиками функций. В вариантах 1–16 ось вращения Ox , в вариантах 17–30 ось вращения Oy .  Решение: Составим чертеж. Фигура, которая вращается вокруг оси OY, окрашена синим цветом. Из графика видны пределы интегрирования по Y: [0;1]. Найдем функцию, обратную  описывает часть параболы, лежащей левее точки x=1. Тогда искомый объем тела вращения можно представить как разность объемов тел вращения V1 правой ветки параболы ( и V2 левой ветки   Объем тела вращения в общем случае вычисляется по формуле:      |