реферат по тфкп. Реферат по теме Конформные отображения
 Скачать 0.66 Mb.
|
|
Министерство образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Нижегородский Государственный Технический Университет им. Р.Е. Алексеева» Кафедра «Прикладная математика» Реферат по теме «Конформные отображения» Выполнила: Студентка 2 курса ИРИТ, группа 10 – ПМ Багрова Екатерина Проверил: Алексеенко С. Н. Нижний Новгород, 2012 г. Содержание
1. Геометрический смысл производной функции комплексного переменного.
Напомним вначале некоторые сведения о кривых. Каждая кривая на плоскости может быть задана параметрическими уравнениями x = x (t), y = y (t), α ≤ t ≤ β , (1) где x (t), y (t) — действительные функции действительного переменного t. В дальнейшем предполагается, что эти функции имеют непрерывные производные на интервале (α, β), причем x’(t) и y’(t) не обращаются в нуль одновременно. Кривая, обладающая указанными свойствами, называется гладкой. Так как каждая точка (х, у) на плоскости задается комплексным числом z = х + iy, то уравнения (1) можно записать в более компактной форме: z (t) = x (t) + i y (t), α ≤ t ≤ β. 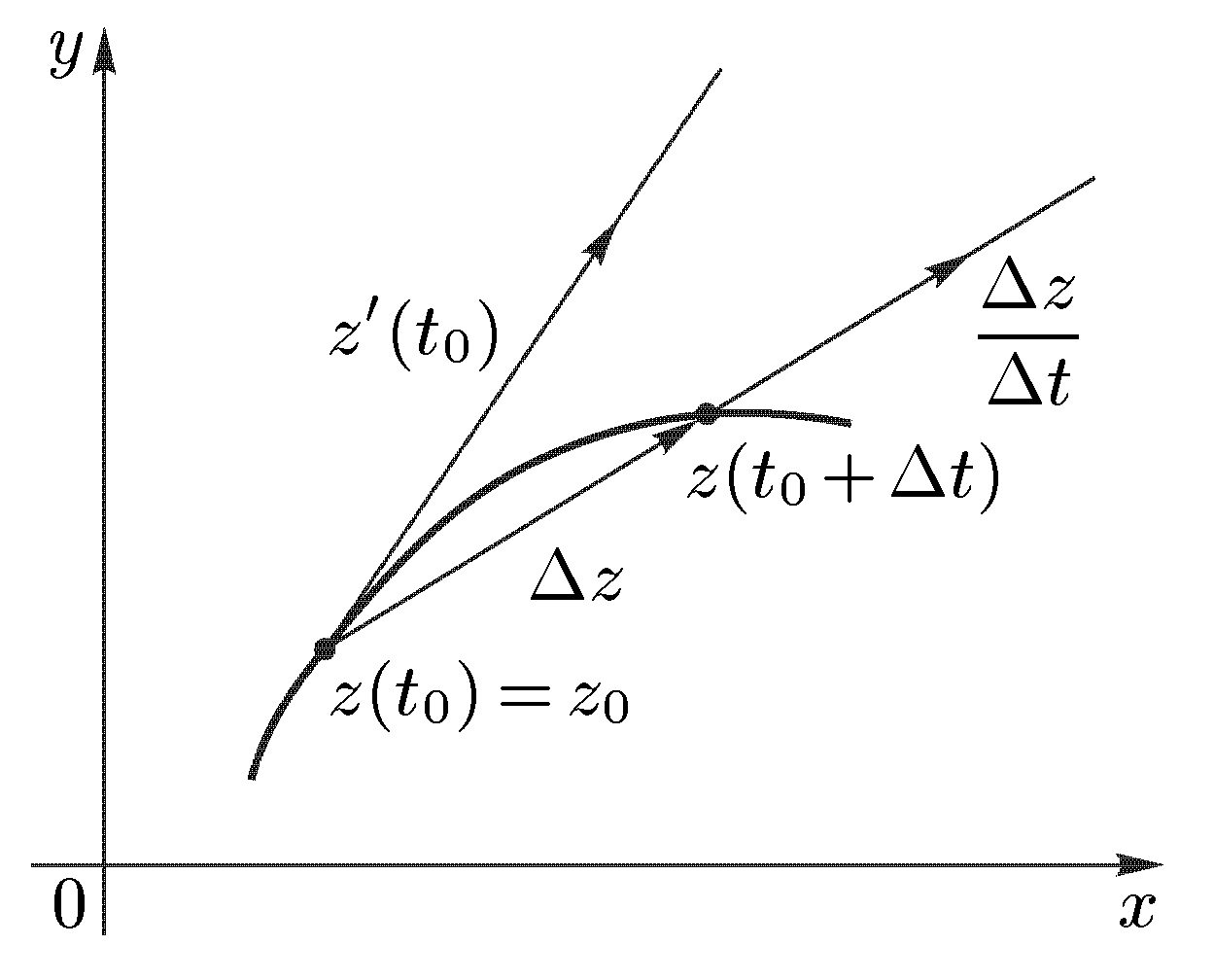 Возьмем значения t0 и t0 + Δt из интервала (α, β). Им соответствуют точки z (t0) и z (t0 + Δ t) на кривой. Вектор Δz = z (t0 + Δt) – z (t0) = Δx + i Δy направлен по секущей, проходящей через эти точки. Если умножить Δz на действительное число 1/ Δt, то получим вектор Δz / Δt, коллинеарный вектору Δz. Начнем уменьшать Δt. Тогда точка z (t0 + Δt) будет приближаться к z (t0) по кривой; вектор Δz/ Δt будет поворачиваться, приближаясь к вектору  .Предельное положение секущих, проходящих через точку z (t0), называется касательной к кривой в этой точке. Таким образом, вектор z ' (t0) направлен по касательной к кривой в точке z (t0). Пусть теперь задана функция f (z), аналитическая в точке z0, причем f ’(z0) ≠ 0. Предположим далее, что через точку z0 проходит кривая γ, заданная уравнением z (t) = x (t) + iy (t), и z (t0) = z0. Кривая γ отображается функцией w = f (z) в кривую Г, лежащую в плоскости переменного w; уравнение кривой Г будет иметь вид w (t) = f (z(t)); точка z0 отобразится в точку w0 = f (z0). По правилу дифференцирования сложной функции w ' (t0) = f ' (z0) · z ' (t0). (2) Отсюда следует, что Arg w ' (t0) = Arg f ' (z0) + Arg z ' (t0). (3) Но z ' (t0) есть вектор, касательный к кривой γ в точке z0 (рис. 1а), a w ' (t0) — вектор, касательный к кривой Г в точке w0 (рис. 1б). Поэтому равенство (3) позволяет придать величине Arg f ' (z0) следующий геометрический смысл: аргумент производной равен углу, на который поворачивается касательная в точке z0 к любой кривой, проходящей через эту точку, при отображении w = f (z). Заметим, что этот угол не зависит от кривой γ, т.е. касательные ко всем кривым, проходящим через точку z0, поворачиваются при отображении w = f (z) на один и тот же угол, равный Arg f ' (z0). Возьмем какие-либо две кривые γ и γ1 проходящие через точку z0, и проведем касательные к этим кривым (рис. 1а). При отображении 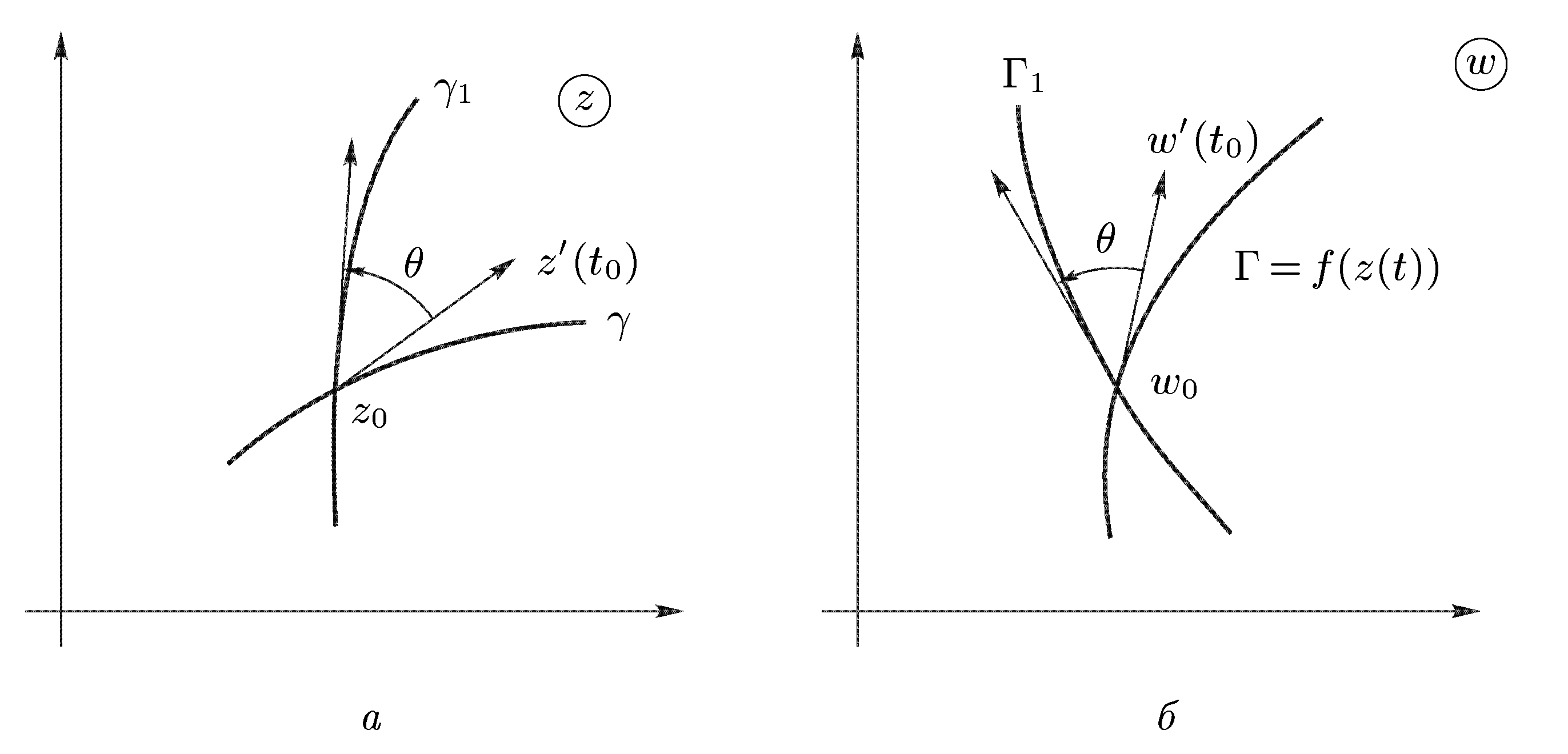 (рис. 1)w = f (z) кривые γ и γ1 перейдут в кривые Г и Г1, а каждая из касательных к γ и γ1 повернется на один и тот же угол. Поэтому угол θ между касательными к γ и γ1 будет равен (как по величине, так и по направлению отсчета) углу между касательными к Г и Г1. Напомним, что углом между кривыми в точке z0 называется угол между касательными к этим кривым в точке z0. Таким образом, если f ’(z0) ≠ 0, то отображение w = f (z) сохраняет углы между кривыми. Заметим, что при этом сохраняется не только абсолютная величина углов между кривыми γ и γ1 и их образами, но и направление углов. Это свойство данного отображения носит название свойства сохранения углов.
Зафиксируем точку z0 и возьмем приращение аргумента Δz; очевидно, что модуль |Δz| равен расстоянию между точками z0 и z = z0 + Δz (рис. 2а). Пусть w = f (z), Δw = w — w0. Тогда величина |Δw| / |Δz| указывает, в каком отношении изменяется расстояние между точками z0 и z в результате отображения w = f (z). Предел 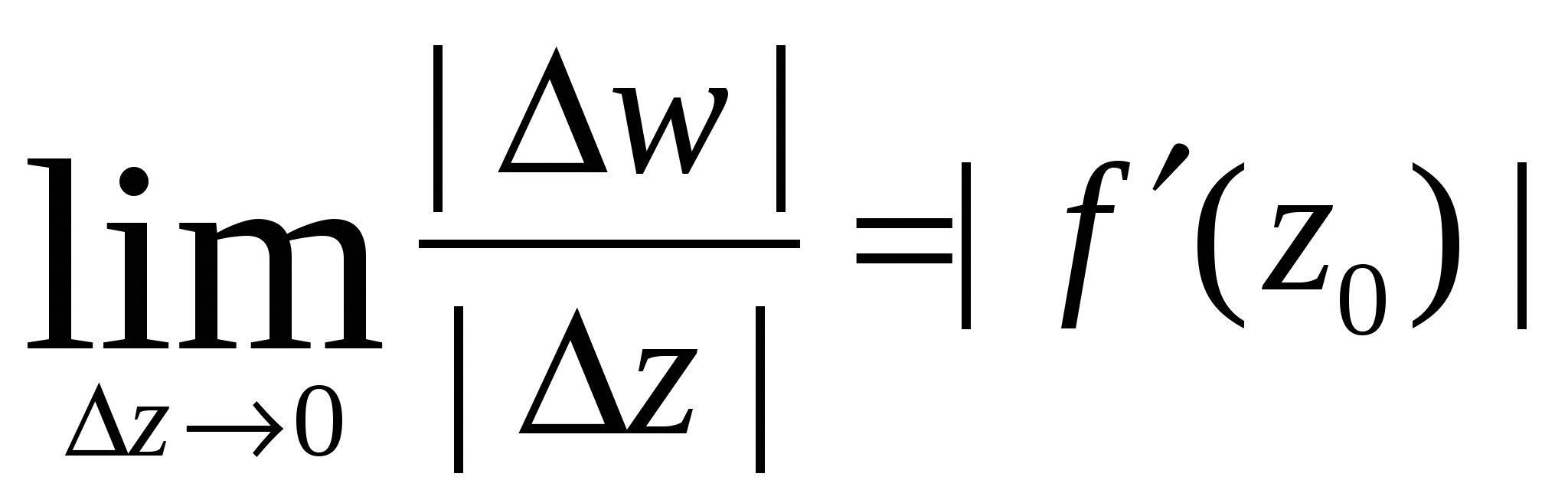 называется коэффициентом растяжения в точке z0 при отображении w = f (z). Поскольку , то модуль | f ’(z0) | равен коэффициенту растяжения в точке z0 при отображении w = f (z). Если | f ’(z0) | > 1, то в достаточно малой окрестности точки z0 расстояния между точками при отображении  (рис. 2)увеличиваются и происходит растяжение; если | f ’(z0)| < 1, то отображение приводит к сжатию (хотя соответствующий коэффициент все равно называют коэффициентом растяжения). Свойство данного отображения носит название свойства постоянного растяжения. Так как производная f '(zo) не зависит от того, по какому пути точка z0 + Δz приближается к z0, то коэффициент растяжения одинаков во всех направлениях. Это свойство можно проиллюстрировать следующим образом. Возьмем окружность l с центром z0 и радиусом |Δz| (т.е. приращения Δz имеют фиксированный модуль, но различные направления — рис. 2а). При отображении w = f (z) эта окружность перейдет в кривую L (рис. 2б); расстояние от точки w = f (z0 + Δz) этой кривой до точки w0 = f (z0) равно |Δw| = |w- w0| = |f (z 0 + Δz) – f (z0)|. Поскольку Δw = f ' (z0) Δz + α (Δz) Δz, где α (Δz) → 0 при Δz → 0, то |w - w0| = |f ' (z0) Δz + α(Δz) Δz|. Это равенство означает, что точки кривой L будут мало отличаться от окружности |w — w0| = |f ' (z0)| | Δz| с центром w0 и радиусом |f ' (z0)| | Δz| (точнее говоря, будут отличаться от этой окружности на величину более высокого порядка малости, чем |Δz| — рис. 2б). 2. Понятие конформного отображения. Отображение называется конформным в точке z0, если: 1) при этом отображении сохраняются углы между любыми двумя кривыми, проходящими через точку z0; 2) растяжение в точке z0 не зависит от направления. Если конформное отображение сохраняет и направление отсчета углов, то оно называется конформным отображением первого рода; если направление отсчета углов меняется на противоположное, то конформным отображением второго рода. Полученные выше результаты сформулируем в виде теоремы. Теорема 1. Если функция w = f (z) является аналитической в точке z0 и f ’(z0) ≠ 0, то f (z) осуществляет конформное отображение первого рода в точке z0. При этом Arg f ' (z0) означает угол поворота, a |f ' (z0)| — коэффициент растяжения при данном отображении. Пример конформного отображения второго рода дает функция (не аналитическая!) w =  , которая каждую область D отображает на область Е, симметричную D относительно оси ОХ. Если f '(z0) = 0, то отображение, вообще говоря, уже не будет конформным в точке z0. Так, отображение w = z2 увеличивает вдвое углы между лучами в начале координат. Отметим, что в силу общих свойств аналитических функций в окрестности точки w0 определена однозначная аналитическая функция z = φ ( w). Тем самым между окрестностями точек z0 и w0 установлено взаимно однозначное соответствие. Введем следующее фундаментальное определение. Определение. Взаимно однозначное отображение области ϑ комплексной плоскости z на область G комплексной плоскости w называется конформным, если это отображение во всех точках z  ϑ обладает свойствами сохранения углов и постоянства растяжений.Подчеркнем, что данное определение подразумевает непрерывность рассматриваемого отображения. Выясним теперь какими свойствами должна обладать функция комплексной переменной для того, чтобы отображение, осуществляемое этой функцией, было конформным. Имеет место следующая теорема. Теорема 2. Пусть функция f (z) является однозначной и однолистной аналитической функцией в области ϑ и f ’ (z) ≠ 0 при z ϑ. Тогда функция f (z) производит конформное отображение области ϑ на область G комплексной плоскости w, представляющую собой область значений функции w = f (z) при z ϑ.Доказательство. Действительно, в силу условия f ’ (z) ≠ 0 при z ϑ отображение, осуществляемое функцией f (z), во всех точках области ϑ обладает свойствами сохранения углов и постоянства растяжений, что и доказывает теорему.Итак, условия аналитичности, однолистности и отличия от нуля производной функции комплексной переменной являются достаточными условиями конформности отображения, осуществляемого этой функцией. Естественно поставить вопрос, являются ли условия необходимыми. На этот вопрос отвечает следующая теорема. Теорема 3. Пусть функция f (z) осуществляет конформное отображение области ϑ комплексной плоскости z на область G комплексной плоскости w и ограничена в ϑ. Тогда функция f (z) является однолистной и аналитической в области ϑ, причем f ’ (z) ≠ 0 при z ϑ.Доказательство. Так как отображение, осуществляемое функцией f (z), является конформным, то оно является взаимно однозначным, и в любой точке z0 ϑ выполняются свойства сохранения углов и постоянства растяжений. Следовательно, для любых точек z1 и z2, принадлежащих окрестности точки z0, с точностью до бесконечно малых величин выполняются соотношения (4)и  , (5)где Δz1 = z1 - z0 и Δz2 = z2 - z0 суть бесконечно малые линейные элементы, выходящие из точки z0, а Δw1 и Δw2 – их образы (р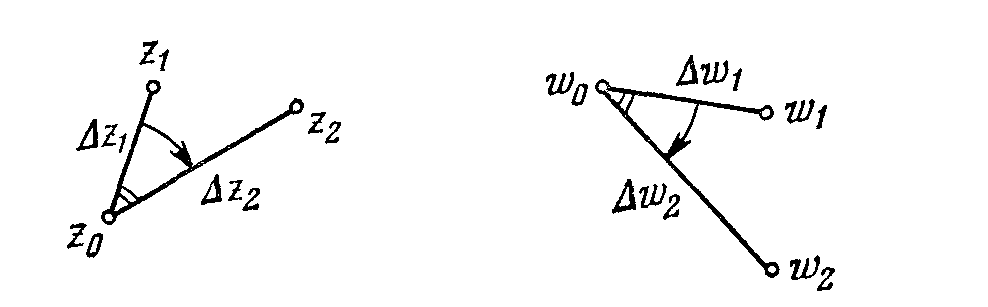ис. 3).  (рис. 3)Заметим, что в силу (4) соответствующие углы в точках z0 и w0 равны не только по абсолютной величине, но и по направлению. Обозначив arg  через , из (4) найдем, что и arg . Действительно,  . (6)Из (5) и (6) получим, что с точностью до бесконечно малых величин имеет место соотношение   .(7)В силу произвольности выбора точек z1 и z2 в окрестности точки z0 соотношение (7) означает, что существует предел разностного отношения  при  . Этот предел по определению является производной функции f (z) в точке z0. Так как  , то эта производная отлична от нуля:  . (8)Точка z0 – произвольная точка области ϑ; поэтому из (8) следует, что функция f (z) является аналитической в области ϑ и f ’ (z) ≠ 0 при z ϑ. Однолистность следует из взаимной однозначности отображения. Теорема доказана.Итак, конформное отображение области ϑ комплексной плоскости z на область G комплексной плоскости w осуществляется только однолистными аналитическими функциями комплексной переменной с производной, отличной от нуля во всех точках области ϑ. Отметим, что условие f ’ (z) ≠ 0 всюду в области ϑ является необходимым, но недостаточным условием конформности отображения области ϑ на область G, осуществляемого функцией f (z). 3. Общие свойства конформных отображений Теорема 4. (теорема Римана). Пусть D и D' — односвязные области на расширенных плоскостях переменных z и w соответственно, причем границы этих областей состоят более чем из одной точки. Тогда существует аналитическая функция, взаимно-однозначно и конформно отображающая D на D'. Из теоремы Римана следует, что односвязную область D нельзя конформно отобразить на единичный круг |w| < 1 только в двух случаях: а) если D есть вся расширенная плоскость  (граница — пустое множество); б) если D есть расширенная плоскость, из которой удалена только одна точка (например, если D — конечная плоскость С, когда из удалена точка z = ∞). Отображение w = f (z) области D на D', существующее по теореме Римана, не является единственным. Для однозначного определения конформного отображения нужно задать дополнительные условия, называемые условиями нормировки, содержащие три действительных параметра. Например, достаточно в какой-либо одной точке z0 области D задать значения w0 = f(z0),  . (9) Здесь в качестве параметров выступают две координаты точки w0 и действительное число  . Условия (9) означают, что отображение w = f(z) является единственным, если для какой-либо точки z0 области D задать ее образ w0 в области D' и угол поворота бесконечно малых векторов в точке z0. Можно задавать и другие условия нормировки, отличные от (9). Например, задают образы одной внутренней и одной граничной точек области D: f(z0) = w0, f(z1) = w1, где z0, w0 — внутренние точки областей D, D', a z0, w0 — граничные точки этих областей. Здесь также присутствуют три действительных параметра: две координаты точки w0 и положение граничной точки w1, которая определяется одним действительным числом (например, расстоянием, отложенным по границе области D' от некоторой фиксированной граничной точки). Укажем еще один вариант условий нормировки: f(zk) = wk, k = 1,2,3, где zk и wk — граничные точки областей D и D'. Сформулируем следующее важное свойство конформных отображений. |