Основы дифференциал. 4.Основы дифференциального и интегрального исчисления, дифференц. 4. основы дифференциального и интегрального исчисления, дифференциальные уравнения
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
4.ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ, ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 4.1.Производная, приложения производной 4.2.Дифференциал функции 4.3.Неопределенный интеграл 4.4.Определенный интеграл 4.5.Дифференциальные уравнения первого порядка 4.1.Производная, приложения производной Определение: Производной функции y = f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует): 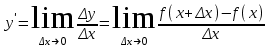 . .Производная функции имеет несколько обозначений: 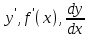 . .Определение: Нахождение производной функции называется дифференцированием этой функции. Определение: Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Определение: Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке. Геометрический смысл производной: Производная 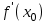 есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой y = f(x) в точке х0, т.е. есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой y = f(x) в точке х0, т.е. 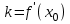 . .Тогда уравнение касательной к кривой y = f(x) в точке х0 примет вид: 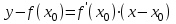 . .Механический смысл производной: Производная пути по времени 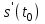 есть скорость точки в момент t0: есть скорость точки в момент t0: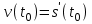 . .Экономический смысл производной: Производная объема произведенной продукции по времени 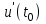 есть производительность труда в момент t0. есть производительность труда в момент t0.Теорема (зависимость между непрерывностью и дифференцируемостью). Если функция y = f(x) дифференцируема в точке х0, то она в этой точке непрерывна. Следствие: Непрерывность функции – необходимое, но не достаточное условие дифференцируемости функции. Замечание: Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором промежутке Х, то функция называется гладкой на этом промежутке. Если же производная функции допускает конечное число точек разрыва (причем первого рода), то такая функция на данном промежутке называется кусочно гладкой. Правила дифференцирования. 1.Производная постоянной величины равна нулю. с'=0 2.Производная аргумента равна 1. х'=1 3.Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций. (u+v)'=u'+v' 4.Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго. (uv)'=u'v+uv' 5.Производная частного двух дифференцируемых функций может быть найдена по формуле 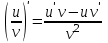 Следствие 1. Постоянный множитель можно вынести за знак производной (сu)'=cu'. Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные (uvw)'=u'vw+uv'w+uvw'. Производная сложной функции. Определение: Пусть переменная у есть функция от переменной u (y=f(u)), а переменная u в свою очередь есть функция от независимой переменной х, то есть задана сложная функция y=f(φ(x)). Теорема: Если y=f(u) и u=φ(x) – дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменой х. y' =f '(u)·u' Производная обратной функции. Определение: Пусть y=f(x) – дифференцируемая и строго монотонная функция на некотором промежутке Х. Если переменную у рассматривать как аргумент, а переменную х как функцию, то новая функция x=φ(y) является обратной к данной и непрерывной на соответствующем промежутке Y. Теорема: Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции 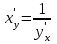 . .Производные основных элементарных функций. 1.Производная логарифмической функции 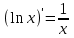 ; ; 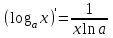 . .2.Производная показательной функции 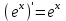 ; ; 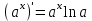 . .3.Производная степенной функции 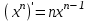 . .4.Производная степенно-показательной функции 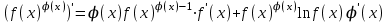 5.Производные тригонометрических функций 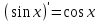 ; ; 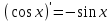 ; ; 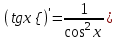 ; ; 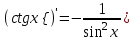 . .6.Производные обратных тригонометрических функций 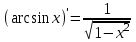 ; ;  ; ; 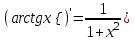 ; ; 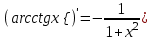 . .Производные высших порядков. Определение: Производная f '(x)от функции f(x), называется производной первого порядка. Но производная f '(x) сама является функцией, которая также может иметь производную. Определение: Производной n-го порядка называется производная от производной (n-1) – го порядка. Обозначение: f '(x), f ''(x), f '''(x),…….f (n)(x),….. Механический смысл второй производной. Если точка движется прямолинейно по закону s=s(t), где s - путь, t – время, то s '(t) представляет скорость изменения пути в момент t0. Следовательно, вторая производная пути по времени s ''(t0)=v'(t0) есть скорость изменения скорости или ускорение точки в момент t0. Основные теоремы дифференциального исчисления. Теорема Ферма: Если дифференцируемая на промежутке Х функция y=f(x) достигает наибольшего или наименьшего значения во внутренней точке х0 этого промежутка, то производная функции в этой точке равна нулю. f '(x0)=0 Геометрический смысл теоремы Ферма: В точке наибольшего или наименьшего значения, достигаемого внутри промежутка Х, касательная к графику функции параллельна оси абсцисс. Теорема Роля: Пусть функция y=f(x) удовлетворяет следующим условиям: 1.непрерывна на отрезке [α, b]; 2.дифференцируема на интервале (α, b); 3.на концах отрезка принимает равные значения, т.е. f(α)=f(b). Тогда внутри отрезка существует по крайней мере одна такая точка ξ 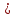 (α, b), в которой производная функция равна нулю: f '(ξ)=0. (α, b), в которой производная функция равна нулю: f '(ξ)=0.Геометрический смысл теоремы Роля: Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс; в этой точке производная и будет равна нулю. Теорема Лагранжа: Пусть функция y=f(x) удовлетворяет следующим условиям: 1.непрерывна на отрезке [α, b]; 2.дифференцируема на интервале (α, b); Тогда внутри отрезка существует по крайней мере одна такая точка ξ 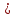 (α, b), в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке т.е. (α, b), в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке т.е. 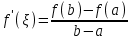 . .Механический смысл теоремы Лагранжа: f(α) - f(b) - это изменение функции на отрезке [α, b]; 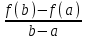 - средняя скорость изменения функции на этом отрезке; - средняя скорость изменения функции на этом отрезке;значения производной в точке – это «мгновенная» скорость изменения функции. Существует хотя бы одна точка внутри отрезка такая, что скорость изменения функции в ней равна средней скорости изменения функции на этом отрезке. Следствие: Если производная функции y=f(x) равна нулю на некотором промежутке Х, то функция тождественно постоянна на этом промежутке. Теорема: (правило Лопиталя): Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле. 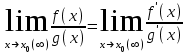 . .Возрастание и убывание функции. Определение: Функция y=f(x) называется возрастающей (убывающей) на промежутке Х, если для любых х1,х2 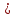 Х, х1<х2 верно неравенство f(х1) Х, х1<х2 верно неравенство f(х1)Определение: Строго возрастающие или убывающие функции называются монотонными. Теорема: (достаточное условие возрастания функции) Если производная дифференцируемой функции положительно внутри некоторого промежутка Х, то она возрастает на этом промежутке. Теорема (достаточное условие убывания функции) Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке. Геометрическая интерпретация условия монотонности: Если касательные к кривой в некотором промежутке направлены под острыми углами к оси абсцисс, то функция возрастает, если под тупыми, то убывает. Теорема (необходимое условие монотонности) Если функция возрастает (убывает) на некотором промежутке Х то можно лишь утверждать, что производная неотрицательна (не положительна) на этом промежутке (в отдельных точках производная монотонной функции может равняться нулю). Экстремум функции. Определение: Точка х0 называется точкой максимума функции y=f(x), если в некоторой окрестности точки х0 выполняется неравенство f(х)≤f(х0). Определение: Точка х1 называется точкой минимума функции y=f(x), если в некоторой окрестности точки х1 выполняется неравенство f(х)≥f(х1). Определение: Значения функции в точках х0 и х1 называются соответственно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием экстремума функции. Определение: Экстремум функции часто называют локальным экстремумом, это говорит о том, что понятие экстремума связано лишь с достаточно малой окрестностью точки х0. Теорема: (необходимое условие экстремума) Для того, чтобы функция y=f(x) имела экстремум в точке х0, необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала. Определение: Точки, в которых выполнено необходимое условие экстремума называются критическими или стационарными (они должны входить в область определения функции). Следствие: Если в какой-либо точке имеется экстремум, то эта точка стационарная. Обратное утверждение не верно. Стационарная точка вовсе не обязательно является точкой экстремума. Теорема: (первое достаточное условие экстремума) Если при переходе через точку х0 производная дифференцируемой функции y=f(x) меняет свой знак с плюса на минус, то точка х0 есть точка максимума функции y=f(x), а если с минуса на плюс, - то точка минимума. Теорема: (второе достаточное условие экстремума) Если первая производная f '(x) дважды дифференцируемой функции равна нулю в некоторой точке х0, а вторая производная в этой точке f ''(x0) положительна, то х0 есть точка минимума функции f '(x); если f ''(x0) отрицательна, то х0 – точка максимума. Схема исследования функции y=f(x) на экстремум: 1.Найти производную у'= f '(x). 2.Найти критические точки функции, в которых производная f '(x)=0 или не существует. 3.Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции. 4.Найти экстремумы функции. Наибольшее и наименьшее значение функции на отрезке. Теорема Вейерштрасса: Если функция y=f(x) непрерывна на отрезке [α,b], то она принимает на нем наибольшее и наименьшее значения. Замечание: Наибольшее и наименьшее значение функции может достигаться как в точках экстремума, так и в точках на концах отрезка. Схема отыскания наибольшего и наименьшего значения функции на отрезке. 1.Найти производную f '(x). 2.Найти стационарные точки функции, в которых f '(x)=0 или не существует. 3.Найти значения функции в стационарных точках и на концах отрезка и выбрать из них наибольшее и наименьшее. Замечание: Если функция y=f(x) непрерывна на интервале (α,b), то она может не принимать на нем наибольшее и наименьшее значения. Частный случай: Если дифференцируемая функция на интервале (α,b) имеет лишь одну точку максимума (или одну точку минимума), то наибольшее (или наименьшее) значение функции совпадает с максимумом (или минимумом) этой функции. Выпуклость функции. Определение: Функция y=f(x) называется выпуклой вниз на промежутке Х, если для любых двух значений х1, х2 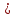 Х из этого промежутка выполняется неравенство Х из этого промежутка выполняется неравенство 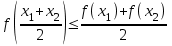 Определение: Функция называется выпуклой вверх на промежутке Х, если для любых двух значений х1, х2 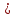 Х из этого промежутка выполняется неравенство Х из этого промежутка выполняется неравенство 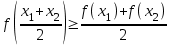 Замечание: Если функция выпукла вниз, то отрезок, соединяющий любые две точки графика, целиком лежит над графиком; если – выпукла вверх, то весь такой отрезок целиком лежит под графиком функции. Теорема: Функция выпукла вниз (вверх) на промежутке Х тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает (убывает). Геометрический смысл теоремы: Если f '(x) возрастает (убывает) на промежутке Х, то возрастает (убывает) угол наклона касательных к графику функции y=f(x). Теорема: (достаточное условие выпуклости) Если вторая производная дважды дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка Х, то функция выпукла вниз (вверх) на этом промежутке. Теорема: (необходимое условие выпуклости) Если функция выпукла на промежутке Х, то можно утверждать лишь, что f ''(x)≥0 (или f ''(x)≤0), где х 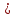 Х. Х.Точки перегиба. Определение: Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх. Теорема (необходимое условие перегиба) Вторая производная f ''(x) дважды дифференцируемой функции в точке перегиба х0 равна нулю. f ''(x0)=0 Теорема (достаточное условие перегиба) Если вторая производная f ''(x) дважды дифференцируемой функции при переходе через некоторую точку х0 меняет свой знак, то х0 есть точка перегиба ее графика. Следствие: Если стационарная точка дифференцируемой функции не является точкой экстремума, то она есть точка перегиба. Схема исследования функции на выпуклость и точки перегиба: 1.Найти вторую производную функции - f ''(x). 2.Найти точки, в которых вторая производная f ''(x)=0 или не существует. 3.Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба 4.Найти значение функции в точках перегиба. Асимптоты графика функции. Определение: Асимптотой графика функции y=f(x) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремиться к нулю при неограниченном удалении точки графика от начала координат. Асимптоты бывают: вертикальные, горизонтальные, наклонные. Нахождение асимптот: Теорема: Пусть функция y=f(x) определена в некоторой окрестности точки х0 (исключая, возможно, саму эту точку) и, хотя бы один из пределов функции при х→х0–0 (слева) или при х→х0+0 (справа) равен бесконечности. Тогда прямая х=х0 является вертикальной асимптотой графика функции y=f(x). Следствие: Вертикальные асимптоты х=х0 следует искать в точках разрыва функции y=f(x) или на концах ее области определения (α,b), если α и b - конечные числа. Теорема: Пусть функция y=f(x) определена при достаточно больших х и существует конечный предел функции 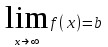 . Тогда прямая у= b есть горизонтальная асимптота графика функции y=f(x). . Тогда прямая у= b есть горизонтальная асимптота графика функции y=f(x).Замечание: Если конечен только один из пределов 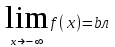 или или 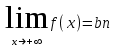 , то функция имеет лишь левостороннюю у= bл или правостороннюю у= bп горизонтальную асимптоту. , то функция имеет лишь левостороннюю у= bл или правостороннюю у= bп горизонтальную асимптоту. Если 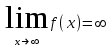 , функция может иметь наклонную асимптоту. , функция может иметь наклонную асимптоту.Теорема: Пусть функция y=f(x) определена при достаточно больших х и существуют конечные пределы 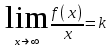 и и 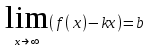 . .Тогда прямая y=kx+b является наклонной асимптотой графика функции y=f(x). Замечание: Наклонная асимптота может быть правосторонней или левосторонней. |
