Основы дифференциал. 4.Основы дифференциального и интегрального исчисления, дифференц. 4. основы дифференциального и интегрального исчисления, дифференциальные уравнения
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
4.5.Дифференциальные уравнения первого порядка Определение: Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких – то уравнением в частных производных. В общем случае дифференциальное уравнение можно записать в виде 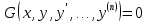 где G – некоторая функция от 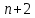 переменных, переменных, 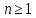 , при этом порядок , при этом порядок 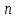 старшей производной входящей в запись уравнения, называется порядком дифференциального уравнения. старшей производной входящей в запись уравнения, называется порядком дифференциального уравнения.Решением дифференциального уравнения 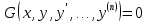 называется такая функция называется такая функция 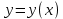 которая при подстановке ее в это уравнение обращает его в тождество. Например, функция которая при подстановке ее в это уравнение обращает его в тождество. Например, функция 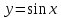 является решением уравнения является решением уравнения 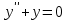 , так как , так как 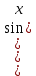 для любых для любых 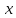 . Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой. . Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.Пример: Решить уравнение 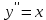 . .Решение: 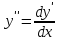 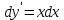 выполнит почленное интегрирование, получаем выполнит почленное интегрирование, получаем 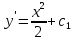 запишем обе части равенства в дифференциалах запишем обе части равенства в дифференциалах 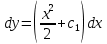 проинтегрируем обе части равенства, получаем проинтегрируем обе части равенства, получаем 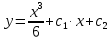 , где , где 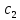 - произвольная постоянная. - произвольная постоянная.Замечание: данное дифференциальное уравнение задает семейство интегральных кривых на плоскости. Для выделения однозначно определенной интегральной кривой в данном случае достаточно указать точку плоскости, через которую проходит интегральная кривая и направление, в котором она проходит через эту точку. Эти дополнительные условия обычно называют начальными, поскольку часто дифференциальные уравнения используются для описания динамических процессов. В этих случаях переменная 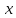 обозначает время. Например, если известно, что обозначает время. Например, если известно, что 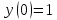 и и  то приходим к решению то приходим к решению 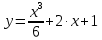 Для выделения однозначно определенного решения дифференциального уравнения 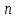 – го порядка, следует дополнительно задать – го порядка, следует дополнительно задать 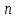 начальных условий. начальных условий.Определение: Общим решением дифференциального уравнения 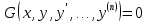 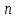 – го порядка называется такое его решение – го порядка называется такое его решение 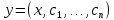 которое является функцией переменной которое является функцией переменной 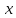 и и 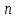 произвольных независимых постоянных произвольных независимых постоянных 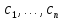 (независимость постоянных означает отсутствие каких-либо соотношений между ними). (независимость постоянных означает отсутствие каких-либо соотношений между ними).Определение: Частным решением дифференциального уравнения, называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных 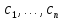 . .Пример: Найти уравнения кривых, в каждой точке которых отрезок касательной, заключенный между осями координат, делится пополам точкой касания. Решение: Пусть 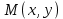 – произвольная точка кривой указанного типа; – произвольная точка кривой указанного типа; 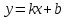 касательная к кривой в точке М; касательная к кривой в точке М; 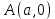 и и 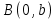 – точки пересечения касательной с осями абсцисс и ординат соответственно. – точки пересечения касательной с осями абсцисс и ординат соответственно. 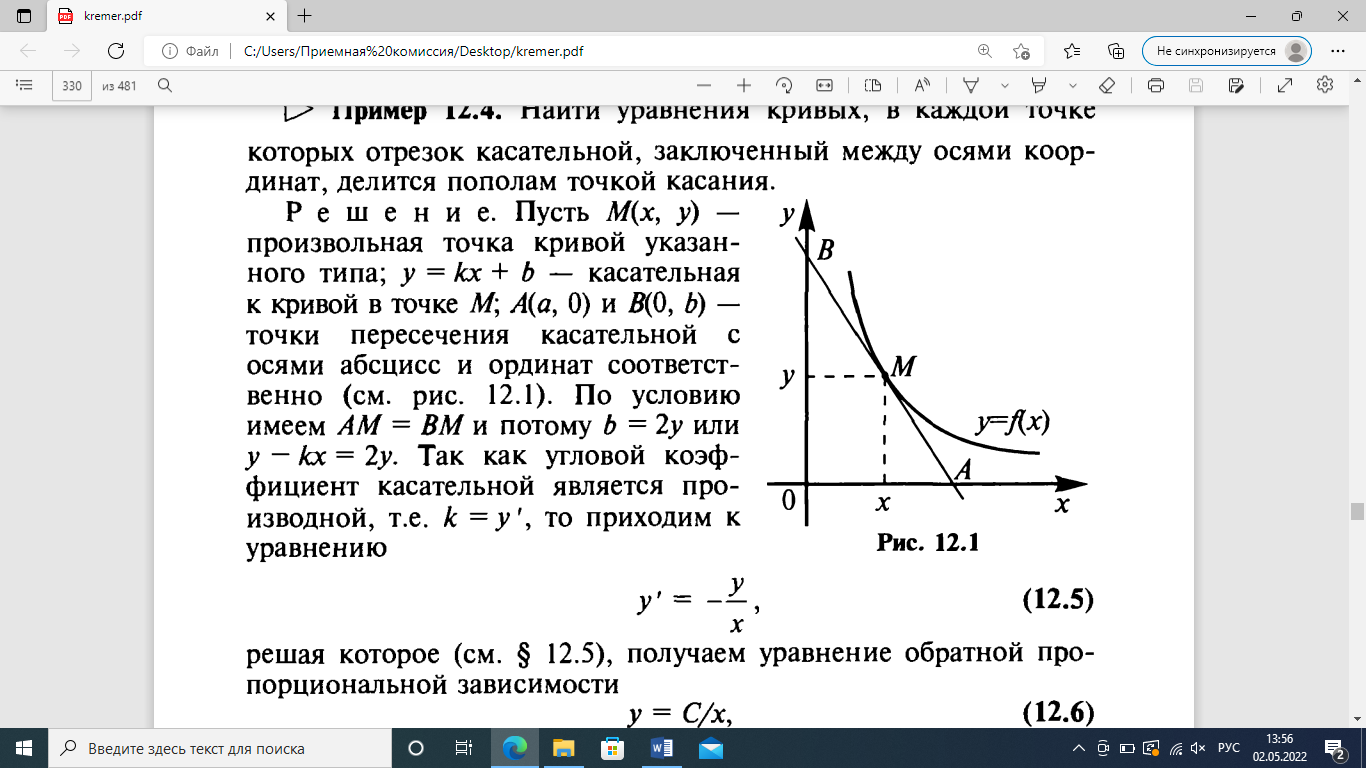 По условию 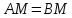 и и 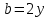 или или  . Так как . Так как  , то приходим к уравнению вида , то приходим к уравнению вида 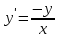 , решение данного уравнения , решение данного уравнения 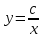 , где с-некоторое число. , где с-некоторое число.Элементы качественного анализа дифференциальных уравнений первого порядка. Определение: Дифференциальное уравнение 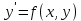 называется автономным если функция называется автономным если функция 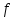 зависит только от переменной зависит только от переменной 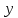 , то есть уравнение имеет вид , то есть уравнение имеет вид 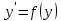 . . Уравнения такого вида часто применяются на практике, например, если дифференциальное уравнение описывает динамическое действие некоторого закона природы, который не будет изменяться со временем 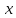 . Предполагается, что уравнение . Предполагается, что уравнение 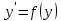 описывает процесс движения точки по прямой описывает процесс движения точки по прямой 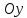 , которая называется фазовой прямой (переменная , которая называется фазовой прямой (переменная 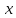 обозначает время). В этом случае обозначает время). В этом случае 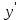 – это скорость движения точки. В соответствии с уравнением – это скорость движения точки. В соответствии с уравнением 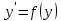 она зависит только от координаты точки и не зависит от значения текущего момента времени. Особую роль в проводимом анализе будут играть нули функции она зависит только от координаты точки и не зависит от значения текущего момента времени. Особую роль в проводимом анализе будут играть нули функции 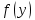 . Убедимся в том, что если . Убедимся в том, что если 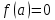 и точка в некоторый момент времени имеет координату и точка в некоторый момент времени имеет координату 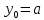 то с течением времени то с течением времени 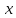 . она не меняет своего положения на фазовой прямой (оси . она не меняет своего положения на фазовой прямой (оси 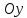 ). (Аналогично, как и во все предшествующие моменты времени она находилась в этой же точке.) Действительно, проверяем подстановкой, что ). (Аналогично, как и во все предшествующие моменты времени она находилась в этой же точке.) Действительно, проверяем подстановкой, что 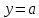 — решение уравнения — решение уравнения 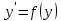 . Но решение . Но решение 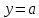 = const как раз и описывает точку, не меняющую с течением времени своего положения. Ввиду изложенных причин нули функции = const как раз и описывает точку, не меняющую с течением времени своего положения. Ввиду изложенных причин нули функции 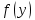 называются также положениями равновесия или стационарными точками. называются также положениями равновесия или стационарными точками.Пусть 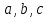 нули функции нули функции 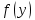 . Прямые . Прямые 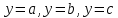 , разбивают всю координатную плоскость на полосы, расположенные параллельно оси абсцисс. Рассмотрим особенности интегральных кривых, заполняющих одну из таких полос. Так как функция , разбивают всю координатную плоскость на полосы, расположенные параллельно оси абсцисс. Рассмотрим особенности интегральных кривых, заполняющих одну из таких полос. Так как функция  непрерывна, то согласно непрерывна, то согласно  . производная . производная  знакопостоянна на произвольном интервале между положениями равновесия. Поэтому все интегральные кривые, лежащие в одной полосе, задаются либо только возрастающими, либо только убывающими функциями. знакопостоянна на произвольном интервале между положениями равновесия. Поэтому все интегральные кривые, лежащие в одной полосе, задаются либо только возрастающими, либо только убывающими функциями.Замечание: При параллельном переносе интегральной кривой вдоль оси абсцисс вновь получается интегральная кривая, причем из того же семейства. Все интегральные кривые одной полосы получаются одна из другой параллельным переносом вдоль оси абсцисс. Прямая  , отвечающая неподвижной точке дифференциального уравнения, является горизонтальной асимптотой интегральных кривых этого уравнения. , отвечающая неподвижной точке дифференциального уравнения, является горизонтальной асимптотой интегральных кривых этого уравнения.Описывая движение точки по фазовой прямой, мы полностью сохраним качественную информацию об этом движении, если вместо интегральных кривых изобразим лишь возможные траектории точки с указанием направления движения. Графическое изображение этих траекторий, называемых фазовыми, дает фазовый портрет автономного уравнения  . Например, фазовый портрет уравнения . Например, фазовый портрет уравнения  изображен на рисунке. изображен на рисунке.В данном случае фазовая прямая 0 у распадается на три траектории: интервалы  и положение равновесия и положение равновесия  . . Пример: Найти фазовый портрет уравнения  . . Решение: Решая уравнение  , получаем положения равновесия: , получаем положения равновесия:  . Траекторий в данном случае будет пять: . Траекторий в данном случае будет пять: интервалы  и точки и точки 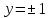 . .Из вида решаемого уравнения следует, что если 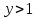 или или 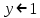 , то , то 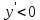 , решение , решение  — убывающая функция, и, следовательно, точка движется по фазовой прямой с уменьшением своей координаты (влево). — убывающая функция, и, следовательно, точка движется по фазовой прямой с уменьшением своей координаты (влево).Если  , то , то  , и точка движется вправо. Окончательный фазовый портрет изображен на рисунке. , и точка движется вправо. Окончательный фазовый портрет изображен на рисунке.Направления движения точки вблизи ее положения равновесия определяют тип положения равновесия. Например, находясь в достаточной близости от точки  , подвижная точка будет лишь приближаться к точке равновесия , подвижная точка будет лишь приближаться к точке равновесия  . . Такие положения равновесия называются устойчивыми. Наоборот, находясь в достаточной близости от точки  , подвижная точка будет лишь удаляться от положения равновесия , подвижная точка будет лишь удаляться от положения равновесия  . . Такие положения равновесия называются неустойчивыми. Возможен также третий тип точек равновесия — так называемые точки полуустойчивого равновесия. Например, точка  уравнения, уравнения,  или точка  уравнения уравнения  Вопросы для самоподготовки: 1.Перечислить основные понятия производной; 2.В чем заключается зависимость между непрерывностью и дифференцируемостью функции. 3.Перечислить правила дифференцирования; 4.Дать определения производной сложной, обратной, 5.Дать определения производной элементарных функций; 6.Дать определение производным высших порядков. 7.Перечислить основные теоремы дифференциального исчисления; правило Лопиталя. 8.Объяснить свойства возрастание и убывание функции; экстремум функции. 9.В чем заключается нахождение наибольшего и наименьшего значения функции на отрезке и интервале; 10.Понятие выпуклость функции; точки перегиба. 11.Рассказать об асимптотах графиков функций. 12.Определить понятие первообразной функции и неопределенного интеграла; 13.Перечислить свойства неопределенного интеграла. 14.Методы интегрирования неопределенного интеграла. 15.Определить понятие определенного интеграла, 16.Охарактеризовать геометрический смысл определенного интеграла 17.Перечислить свойства определенного интеграла; 18.Перечислить геометрические приложения определенного интеграла Практические задания 1.В задачах определить производные  , пользуясь формулами дифференцирования , пользуясь формулами дифференцирования1.1. а) 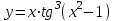 б) б)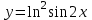 1.2. а) 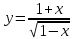 б) б) 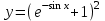 1.3. а) 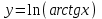 б) б) 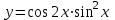 1.4. а) 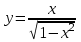 б) б) 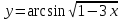 1.5. а) 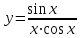 б) б) 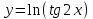 1.6. а) 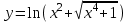 б) б) 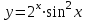 1.7. а) 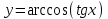 б) б) 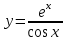 1.8. а) 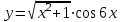 б) б) 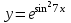 1.9. а) 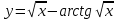 б) б) 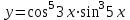 1.10. а) 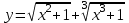 б) б)  1.11. а) 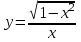 б) б) 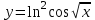 1.12. а) 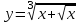 б) б) 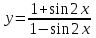 1.13. а) 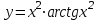 б) б) 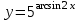 1.14. а) 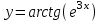 б) б) 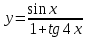 1.15. а) 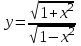 б) б)  |
