Основы дифференциал. 4.Основы дифференциального и интегрального исчисления, дифференц. 4. основы дифференциального и интегрального исчисления, дифференциальные уравнения
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
4.2.Дифференциал функции. На основании теоремы о связи бесконечно малых величин с пределами функций можно записать 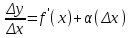 , где α(∆х) – бесконечно малая величина при ∆х→0, откуда , где α(∆х) – бесконечно малая величина при ∆х→0, откуда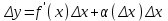 Определение: Дифференциалом функции называется главная линейная относительно ∆х часть приращения функции, равная произведению производной на приращение независимой переменной  Определение: Дифференциал независимой переменной равен приращению этой переменной dx=∆х Формулу для дифференцирования функции можно записать в виде 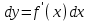 Геометрический смысл дифференциала: Дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y=f(x) в данной точке, когда х получает приращение ∆х. Свойства дифференциала. 1.dc=0 2.d(cu)=c du 3.d(u±v)=du±dv 4.d(uv)=v du+u dv 5. 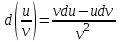 Инвариантность формы дифференциала: Рассмотрим функцию y=f(u), где аргумент u=φ(x) сам является функцией от х, то есть рассмотрим сложную функцию y=f [φ(x)]. Если y=f(u) и u=φ(x) – дифференцируемые функции от своих аргументов, то производная сложной функции равна y' =f '(u)∙u'. Тогда дифференциал функции dy=f '(u)du Данное равенство означает, что формула дифференциала не изменяется, если вместо функции от независимой переменной х рассматривать функцию от зависимой переменой u. Это свойство дифференциала получило название инвариантности (неизменности формы дифференциала). Понятие о дифференциалах высших порядков. Дифференциал независимой переменной имеет произвольное, но фиксированное значение, не зависящее от х. В этом случае dy есть некоторая функция х, которая также может иметь дифференциал. Определение: Дифференциалом второго порядка (или вторым дифференциалом) d2 y функции y=f(x) называется дифференциал от дифференциала первого порядка этой функции, d2 y = d(dy) Дифференциалом n – го порядка (или n – м дифференциалом) dn y называется дифференциал от дифференциала (n-1) – го порядка этой функции dn y=d(dn-1 y) Важные формулы: 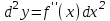 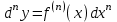 Определение: Дифференциал второго (и вообще n-го) порядка равен произведению производной второго (n-го) порядка на квадрат (n-ю степень) дифференциала независимой переменной.   . .4.3.Неопределенный интеграл. Определение: Функция F(x) называется первообразной функцией для функции f(x) на промежутке Х, если в каждой точке х этого промежутка F'(x)=f(x). Теорема: Если F1(x) и F2(x) – первообразные для функции f(x) на некотором промежутке Х, то найдется такое число С, что будет справедливо равенство F2(x) = F1(x)+С Следствие: Если F(x) – первообразная для функции f(x), то выражение вида F(x)+С, где С – произвольное число. Задает все возможные первообразные для f(x). Определение: Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x) и обозначается 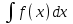 , где , где 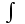 - знак интеграла, f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение. - знак интеграла, f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение.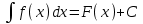 где F(x) – некоторая первообразная для функции f(x), С – произвольная постоянная. Свойства неопределенного интеграла. 1.Производная от неопределенного интеграла равна подынтегральной функции: 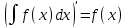 . .2.Дифференциал неопределенного интеграла равен подынтегральному выражению: 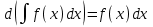 . .3.Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого 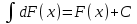 , где С – произвольное число. , где С – произвольное число.4.Постоянный множитель можно вынести за знак интеграла 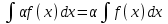 . .5.Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций 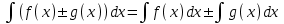 . .Методы интегрирования. 1.Метод замены переменной: 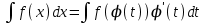 , где х=φ(t) – функция, дифференцируемая на рассматриваемом промежутке. , где х=φ(t) – функция, дифференцируемая на рассматриваемом промежутке.Теорема: Пусть F(x) некоторая первообразная для функции f(x). Тогда 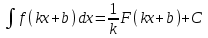 где k и b – некоторые числа, k≠0. где k и b – некоторые числа, k≠0.2.Метод интегрирования по частям: Пусть u=u(x) и v=v(x) – дифференцируемые функции, тогда  - данная формула называется формулой интегрирования по частям. - данная формула называется формулой интегрирования по частям.3.Метод неопределенных коэффициентов: Пример: Найти 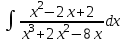 Решение: х3+2х2-8х=х(х+4)*(х+2) 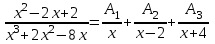 Найдем постоянные А1, А2, А3. Приводя дроби правой части к общему знаменателю, приходим к равенству Найдем постоянные А1, А2, А3. Приводя дроби правой части к общему знаменателю, приходим к равенствуА1(х-2)(х+4)+А2(х+4)х+А3(х-2)х=х2-2х+2 Если х=0, то А1=-1/4. Если х=2, то А2=1/6. Если х=-4, то А3=13/12 (Прием нахождения постоянных А1, А2, А3…. Нетрудно обобщить и использовать для доказательства существования указанного разложения в общем случае.) Тогда 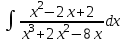 = =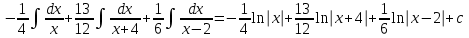 4.4.Определенный интеграл Интегральная сумма: Пусть на [α, b] задана функция y=f(x). Разобьем отрезок [α, b] на n элементарных отрезков точками х0, х1,….хn: α= х0< х1<….<хn =b. На каждом отрезке [хi-1, xi] отрезке разбиения выберем некоторую точку 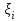 и положим и положим  , где i=1,2,…n. Сумма вида , где i=1,2,…n. Сумма вида 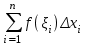 - называется интегральной суммой для функции y=f(x) на [α, b]. - называется интегральной суммой для функции y=f(x) на [α, b].Определение: Пусть предел интегральной суммы 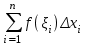 при стремлении при стремлении 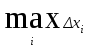 к нулю существует, конечен и не зависит от способа выбора точек х1,х2,…. и точек ξ1, ξ2,….. Тогда этот предел называется определенным интегралом от функции y=f(x) на [α, b] и обозначается к нулю существует, конечен и не зависит от способа выбора точек х1,х2,…. и точек ξ1, ξ2,….. Тогда этот предел называется определенным интегралом от функции y=f(x) на [α, b] и обозначается 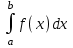 , а сама функция y=f(x) называется интегрируемой на отрезке [α, b]. , а сама функция y=f(x) называется интегрируемой на отрезке [α, b].При этом α – называется нижним пределом, b – верхним пределом, f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, а задача о нахождении 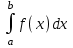 - интегрированием функции f(x) на отрезке [α, b]. - интегрированием функции f(x) на отрезке [α, b].Замечание: 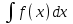 представляет семейство функций, представляет семейство функций, 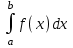 - есть определенное число. - есть определенное число.Геометрический смысл определенного интеграла: В случае когда функция y=f(x) неотрицательна на отрезке [α, b], где α < b, 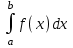 численно равен площади S под кривой y=f(x) на [α, b]. численно равен площади S под кривой y=f(x) на [α, b].Экономический смысл интеграла: Если f(t) – производительность труда в момент t, то 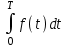 есть объем выпускаемой продукции за промежуток [0,Т]. есть объем выпускаемой продукции за промежуток [0,Т].Величина и объем продукции, произведенной за промежуток времени [0,Т], численно равна площади под графиком функции z=f(t), описывающей изменение производительности труда с течением времени, на промежутке [0,Т]. Теорема: (Достаточное условие существования определенного интеграла). Если функция y=f(x) непрерывна на отрезке [α, b], то она интегрируема на этом отрезке. Свойства определенного интеграла: 1.Постоянный множитель можно вынести за знак интеграла . 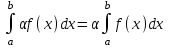 , где , где 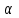 - некоторое число. - некоторое число.2.Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций. 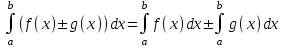 3.Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникающих частей 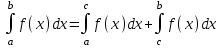 4.Если на отрезке [α, b], где α < b, f(x) ≤ g(х), то и 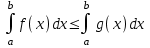 (обе части неравенства можно почленно интегрировать. (обе части неравенства можно почленно интегрировать.Следствие: Пусть на отрезке [α, b], где α < b, где m ≤ f(x) ≤ M, где m и M – некоторые числа. Тогда 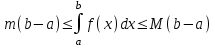 . .5.Теорема о среднем. Если функция y=f(x) непрерывна на отрезке [α, b], где α < b, то найдется такое значение ξ 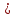 [α, b], что [α, b], что 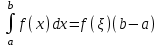 Следствие: Найдется такая точка ξ из отрезка [α, b], что площадь под кривой y=f(x) на [α, b] равна площади прямоугольника со сторонами f(ξ) и (b – α). Определенный интеграл как функция верхнего предела. Определение: Ф (х)= 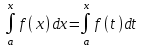 , где х , где х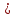 [α, b], а функция Ф(х) называется интегралом с переменным верхним пределом. [α, b], а функция Ф(х) называется интегралом с переменным верхним пределом.Свойства функции Ф(х): 1.Теорема: Если функция y=f(x) непрерывна на отрезке [α, b], то функция Ф(х) так же непрерывна на [α, b]. 2.Теорема: Пусть функция y=f(x) непрерывна на отрезке [α, b]. Тогда в каждой точке х отрезка [α, b] производная функции Ф(х) по переменному верхнему пределу равна подынтегральной функции f(x). Ф' (х)= 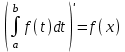 Следствие: Если функция y=f(x) непрерывна на отрезке [α, b], то для этой функции существует первообразная на отрезке [α, b]. Теорема (Формула Ньютона - Лейбница). Пусть функция y=f(x) непрерывна на отрезке [α, b] и F(x) – любая первообразная для f(x) на [α, b]. Тогда определенный интеграл от функции f(x) на [α, b] равен приращению первообразной F(x) на этом отрезке. 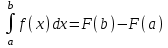 Методы интегрирования. 1.Замена переменной. Теорема: Пусть функция φ(t) имеет непрерывную производную на отрезке [α, b], 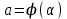 , ,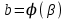 и функция f(x) непрерывна в каждой точке х вида х=φ(t), где t и функция f(x) непрерывна в каждой точке х вида х=φ(t), где t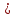 [α, b]. Тогда справедливо следующее равенство [α, b]. Тогда справедливо следующее равенство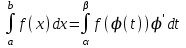 Данная формула носит название формулы замены переменной в определенном интеграле. 2.Интегрирование по частям. Теорема: Пусть функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [α, b]. Тогда 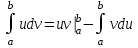 - формула интегрирования по частям для определенного интеграла. - формула интегрирования по частям для определенного интеграла.Пример: Вычислить 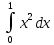 Решение: 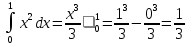 Пример: Вычислить 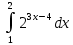 Решение: 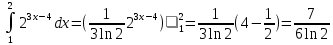 Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур 1.Пусть функция y=f(x) неотрицательна и непрерывна на отрезке [α, b]. Тогда по геометрическому смыслу определенного интеграла площадь S под кривой y=f(x) на [α, b] численно равна определенному интегралу 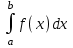 , т.е. , т.е.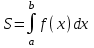 2.Пусть функция y=f(x) неположительна и непрерывна на отрезке [α, b]. Выясним, какая связь в этом случае существует между площадью S криволинейной трапеции «над кривой» y=f(x) на отрезке [α, b] и интеграл 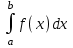 . .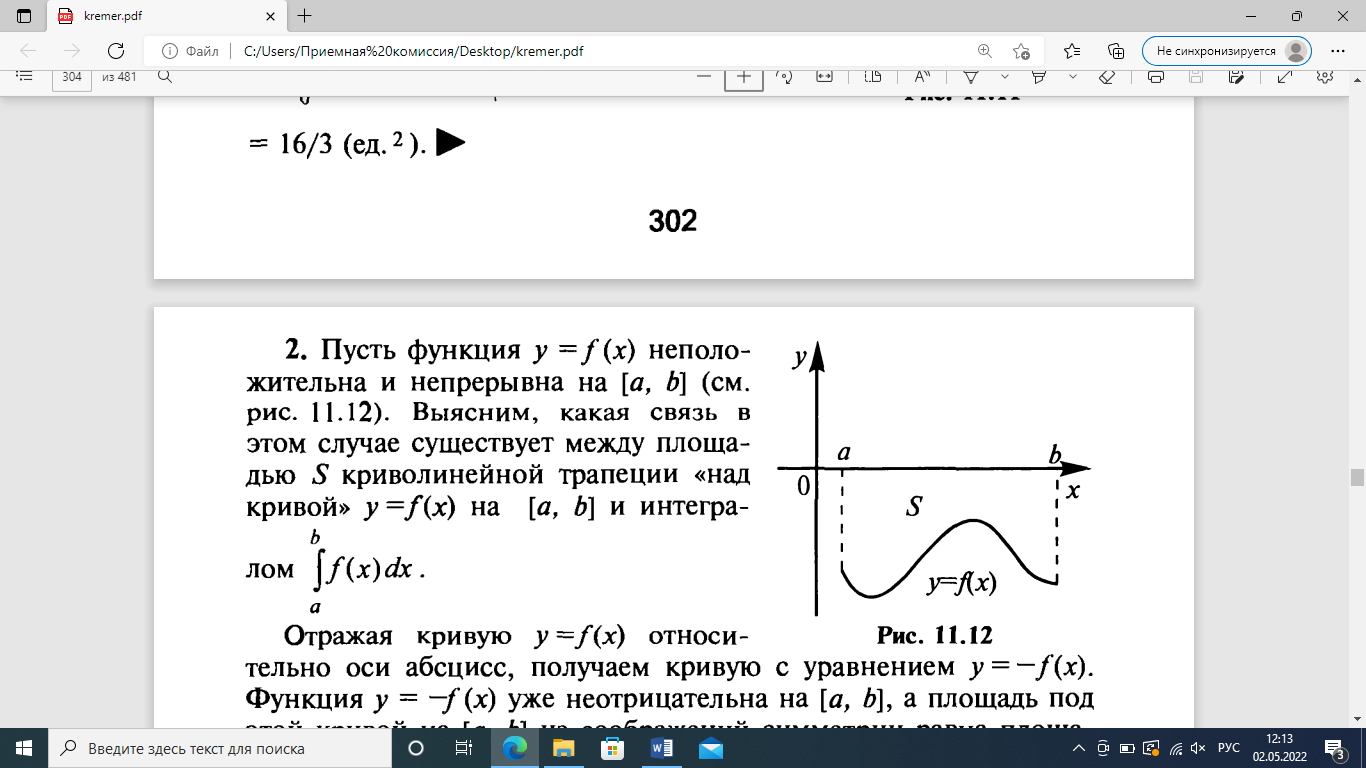 Отражая кривую y=f(x) относительно оси абсцисс, получаем кривую с уравнением y= - f(x). Функция y=f(-x) уже неотрицательна на [α, b], а площадь под этой кривой на [α, b] из соображений симметрии равна площади S. Тогда 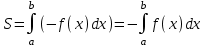 . .Таким образом, если функция y=f(x) неположительна на [α, b], то площадь S над кривой y=f(x) на [α, b] отличается знаком от определенного интеграла 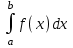 . .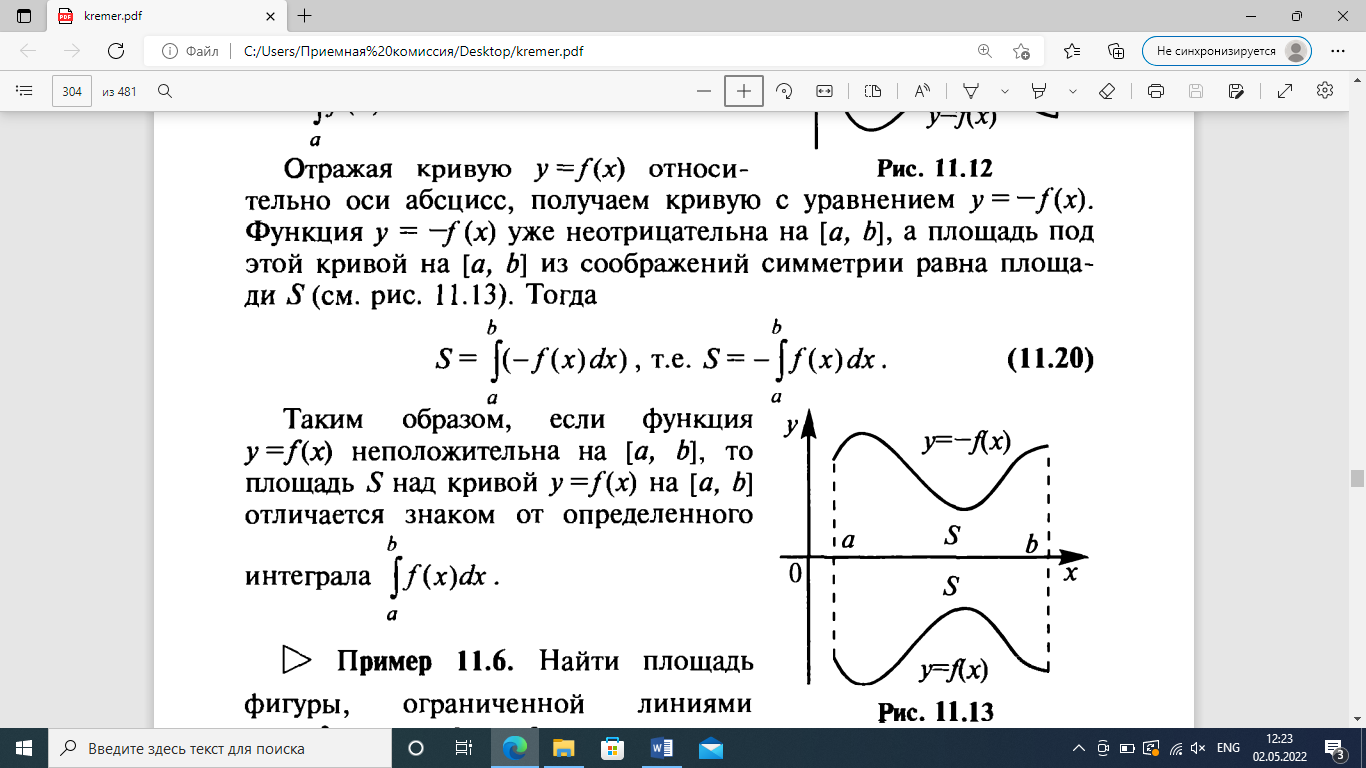 3.Пусть на отрезке [α, b] задана непрерывная функция y=f(x) общего вида. Предположим также, что исходный отрезок можно разбить точками на конечное число интервалов так, что на каждом из них функция y=f(x) будет знакопостоянна или равна нулю. Выясним, какая в данном случае существует связь между определенным интегралом 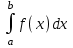 и площадями возникающих криволинейных трапеций. Предположим, что площадь фигуры S=S1+S2+S3, т.е. равна алгебраической сумме соответствующих определенных интегралов: и площадями возникающих криволинейных трапеций. Предположим, что площадь фигуры S=S1+S2+S3, т.е. равна алгебраической сумме соответствующих определенных интегралов: 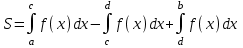 . . 4.Теорема: Пусть на отрезке [α, b] заданы непрерывные функции y=f1(x) и y=f2(x) такие, что f1(x) ≥f2(x). Тогда площадь S фигуры, заключенной между кривыми y=f1(x) и y=f2(x) на отрезке [α, b] вычисляется по формуле 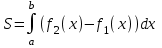 Проиллюстрируем теорему графически. Возможны несколько случаев расположения кривых на отрезке [α, b]. 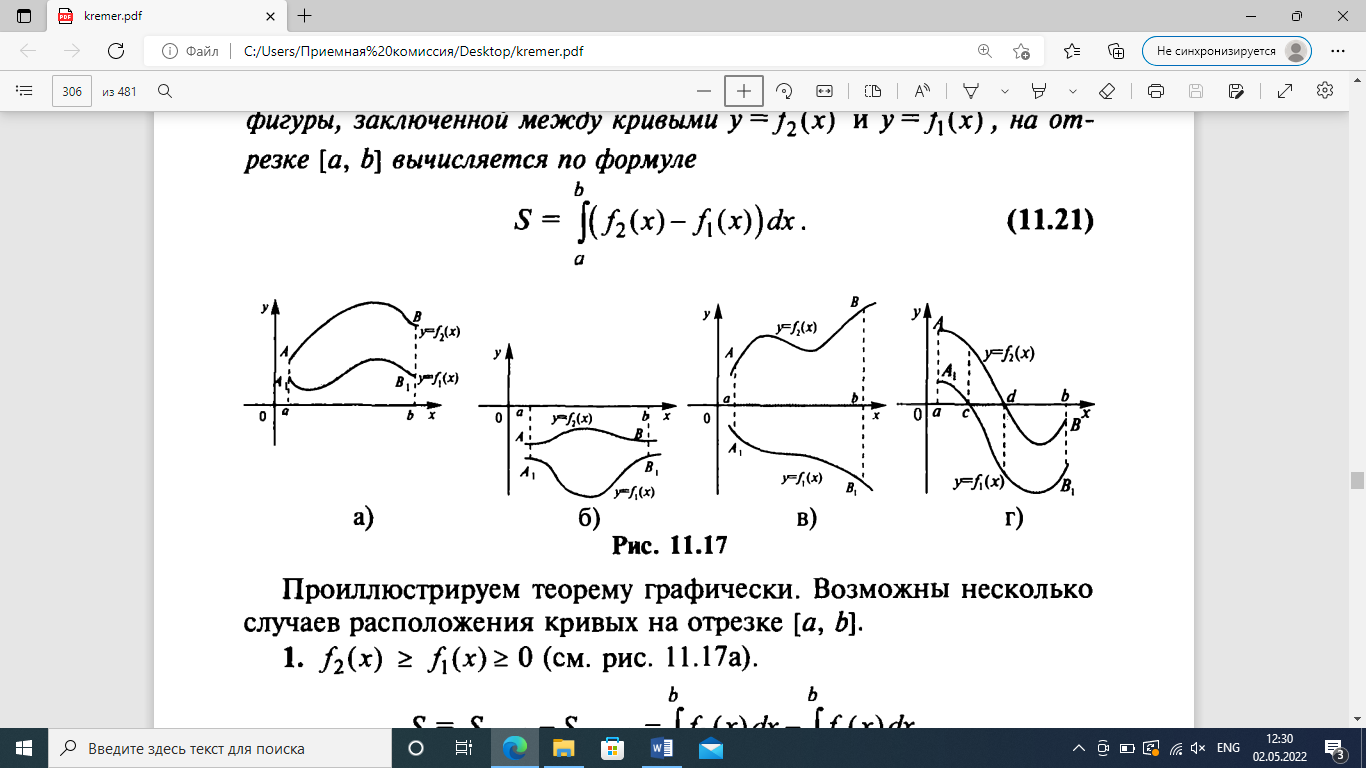 1. 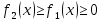 (рис. а) (рис. а)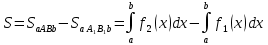 2.  (рис. б) (рис. б)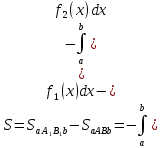 3. 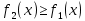 ; ; 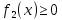 ; ; 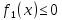 (рис. в) (рис. в)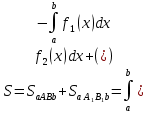 4.Общий случай (рис. г) сводится к частным случаям, рассмотренным выше, если разбить отрезок [α, b] на отдельные отрезки 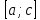 ; ;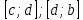 Вычисление объемов тел вращения. 1.Пусть на отрезке [α, b] задана непрерывная знакопостоянная функция y=f(x). Необходимо найти объем Vx тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями y=f(x), у=0, х=α, х=b. 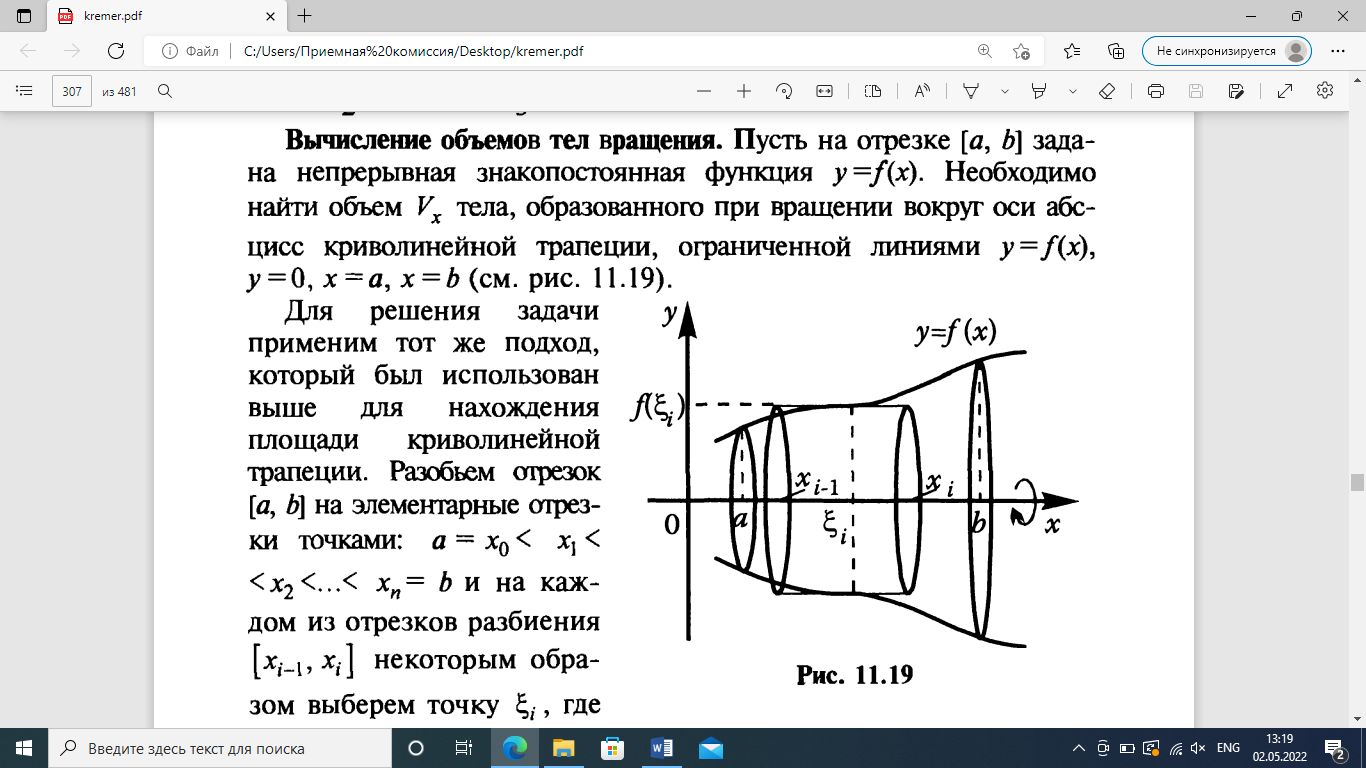 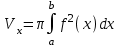 2.Формально заменяя в формуле 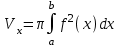 переменную х на у, получаем формулу для вычисления объема Vy тела, полученного от вращения криволинейной трапеции вокруг оси ординат: переменную х на у, получаем формулу для вычисления объема Vy тела, полученного от вращения криволинейной трапеции вокруг оси ординат: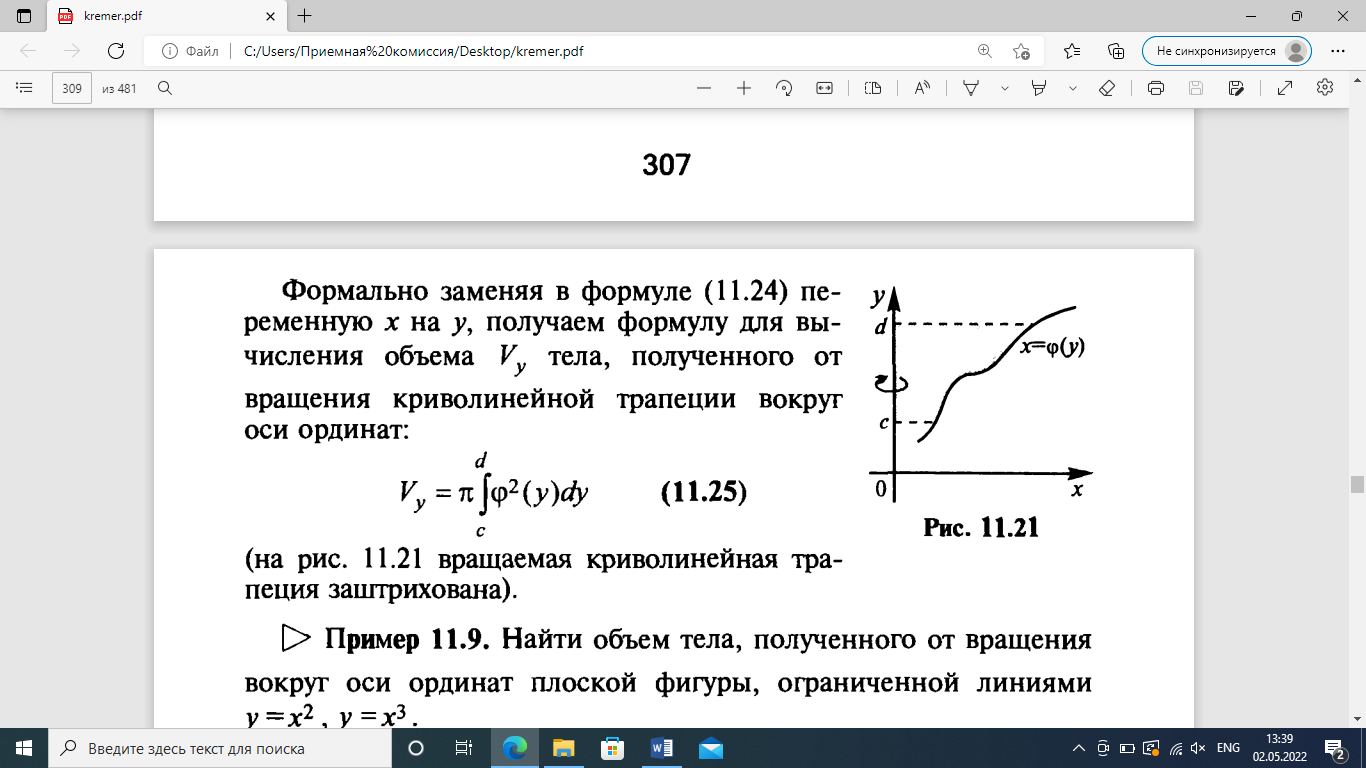 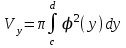 |
