реферат по тфкп. Реферат по теме Конформные отображения

• Название: Реферат по теме Конформные отображения
• Анкор: реферат по тфкп.doc
• Дата: 03.05.2018
• Размер: 0.66 Mb.
• Имя файла: реферат по тфкп.doc
• Тип: Реферат; #18852
• страница: 3 из 3

Теорема 9. Пусть функция w = f(z) однолистна и аналитична в области D, отображает D на область Е и f '(z) ≠ 0. Тогда обратная функция z = g(w) также аналитична в области Е и

(19)

Доказательство. Зафиксируем произвольную точку z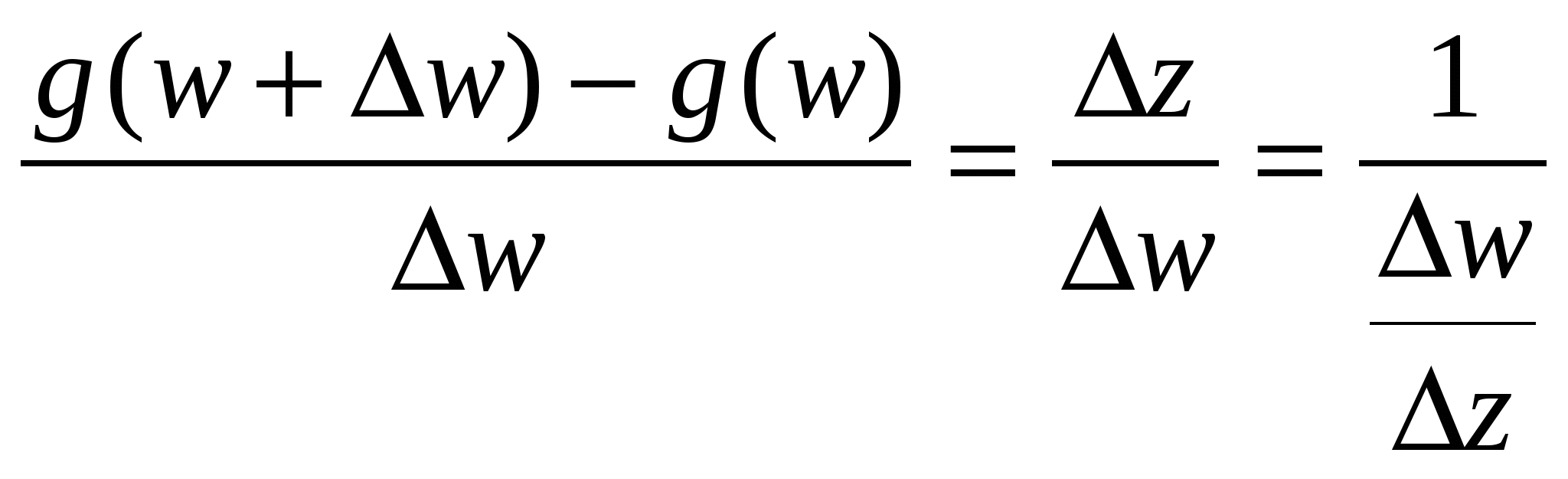D и возьмем приращение Δz ≠ 0. Тогда, в силу однолистности функции w = f(z), соответствующее приращение Δw = f(z + Δz) — f(z) также не равно нулю. Поэтому

Так как функция w = f(z) аналитична, то она непрерывна в точке z.

Следовательно, Δw → 0 при Δz → 0, а в силу взаимной однозначности верно и обратное: Δz → 0 при Δw → 0. Отсюда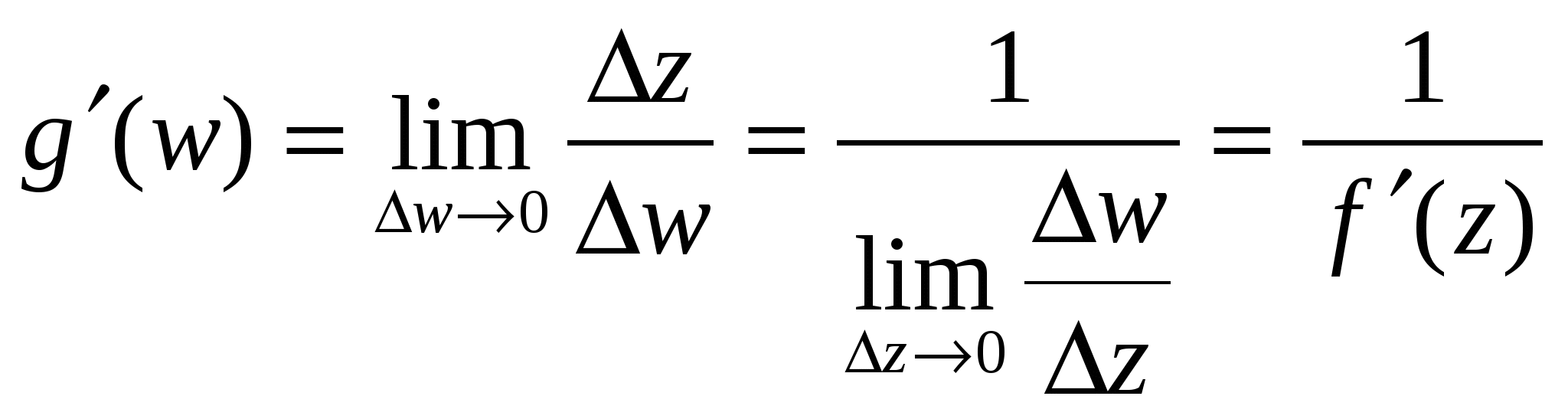



что и требовалось доказать.

Аргументом функции z = g(w), обратной w = f(z), является переменная w. Поскольку аргумент функции часто обозначают через z, то для единообразия переобозначают переменные z и w и пишут w = g(z). Например, обратная функция к w = zⁿ запишется как w = .

Рассмотрим подробнее функцию w = 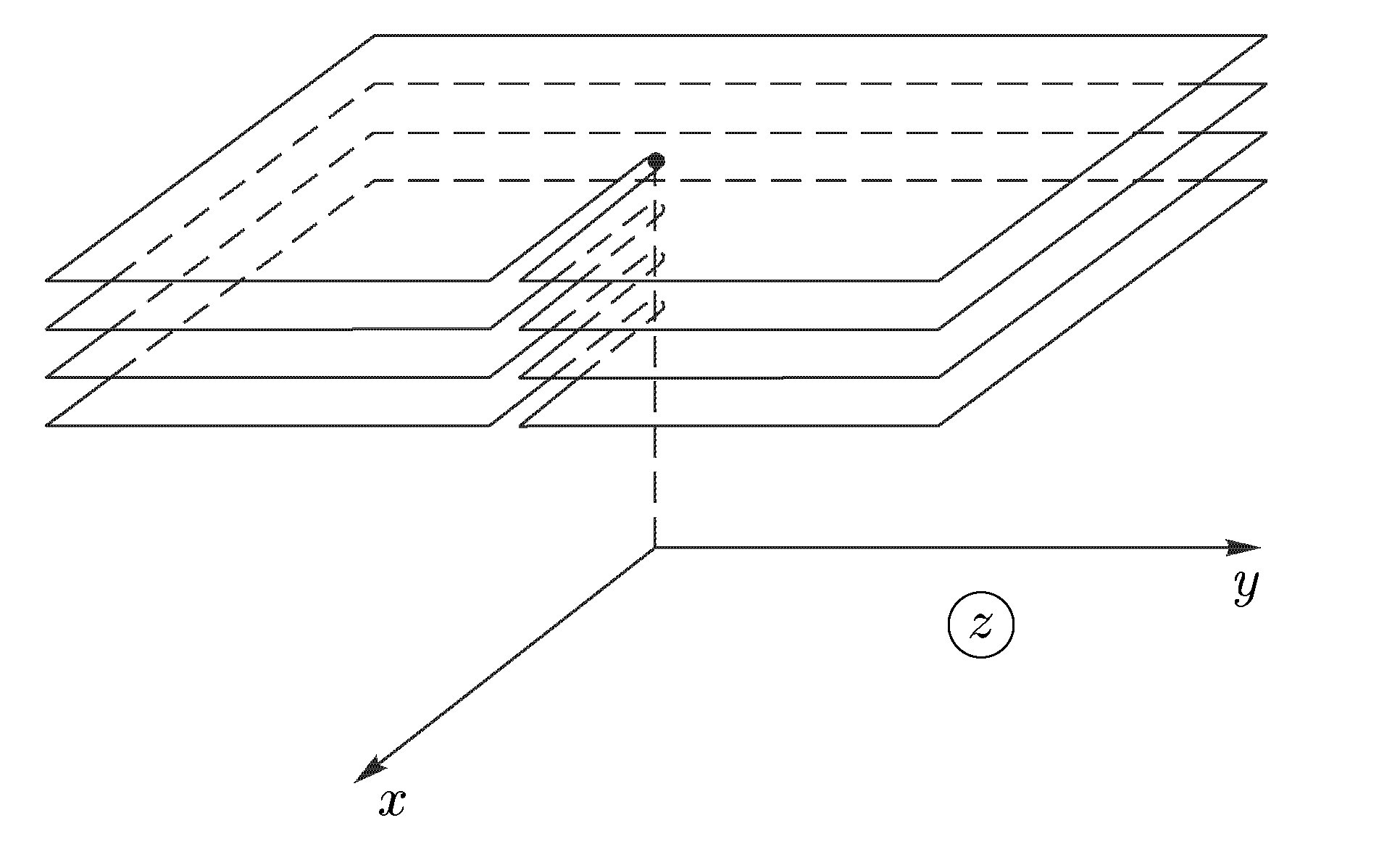. Как было отмечено выше, она является многозначной. Тем не менее можно определить эту функцию на множестве более сложного устройства, чем комплексная плоскость, на котором функция w =станет взаимно-однозначной и непрерывной. Опишем соответствующее множество. Возьмем n экземпляров ("листов") D₀, D₁,..., D_n-1 комплексной плоскости, разрезанной вдоль положительной полуоси, и расположим их друг над другом (на рис. 6а показан случай n = 4).

(рис. 6а)

Затем тот край разреза области D₀, к которому мы подходим снизу от луча ОХ (т.е. по полуплоскости у < 0), склеим с верхним краем разреза области D₁; нижний край разреза области D₁ склеим с верхним краем разреза области D₂ и т.д., пока не склеим нижний край разреза D_n-2 с верхним краем разреза D_n-1. Теперь склеим оставшиеся свободными нижний край разреза области D_n-1 (на рис. 6а это D₃) с верхним краем разреза области D₀. В трехмерном пространстве такую склейку невозможно осуществить без пересечения с уже сделанными склейками промежуточных листов. Но мы условимся считать эту склейку непересекающейся с предыдущими (т.е. точки этой склейки считаются отличными от точек остальных склеек). Полученная поверхность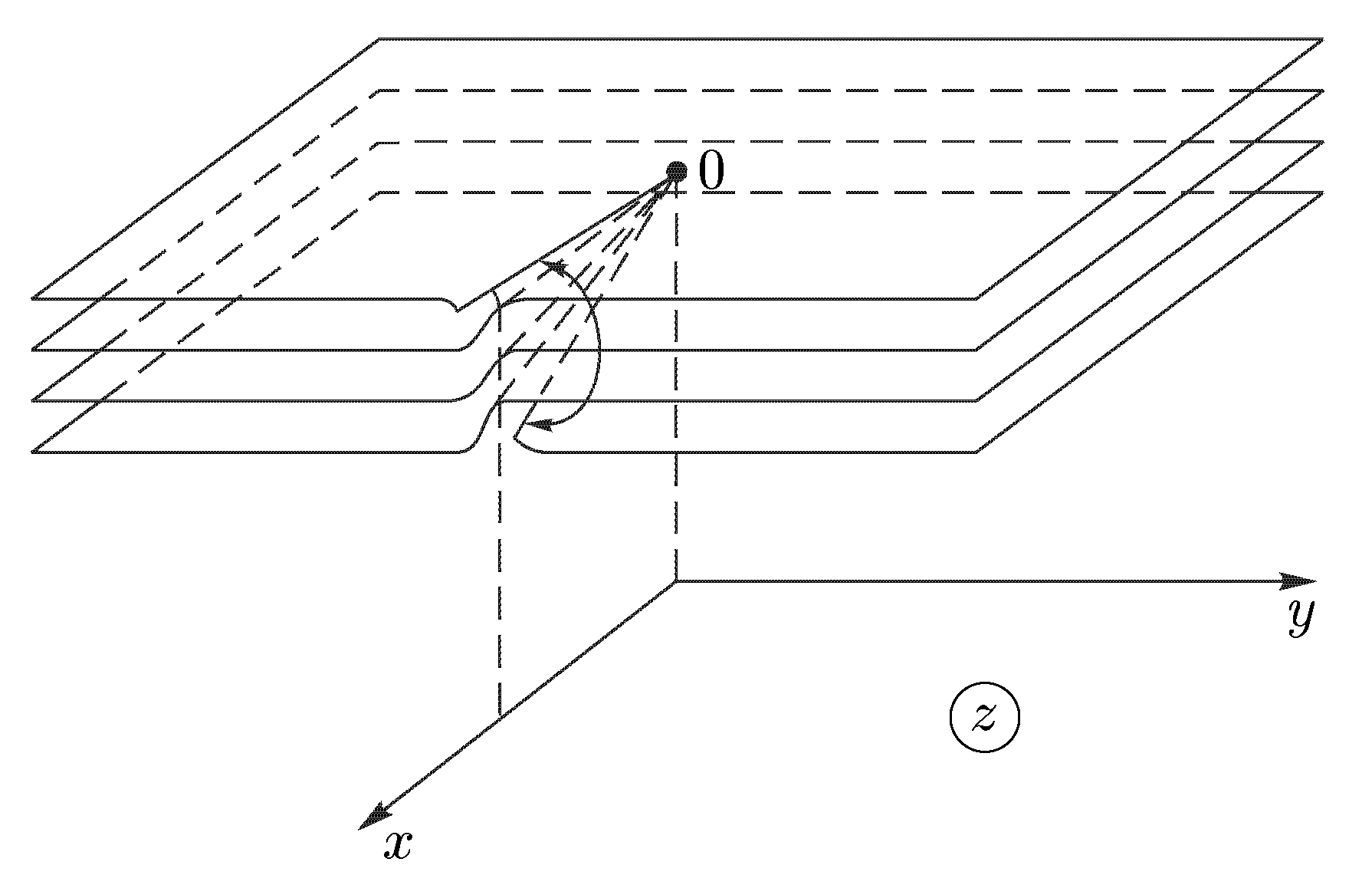

(рис. 6б)

показана на рис. 6б. Она называется римановой поверхностью функции w = . Над каждой точкой комплексной плоскости, отличной от 0 и ∞, расположено ровно n точек римановой поверхности. Точки х > 0 действительной полуоси не составляют исключения, так как все склейки, расположенные над ней, считаются непересекающимися. Лишь две точки не обладают этим свойством: z = 0 и z = ∞.Все листы римановой поверхности считаются склеенными в точках, расположенных над точками z = 0 и z = ∞.

Определим теперь функцию w = на построенной римановой поверхности. Напомним, что если z = r e^iφ, то все корни n-й степени из z определяются формулой (*):

(20)

Угол φ в этой формуле можно выбирать из любого промежутка длины 2π; нам удобно предполагать, что 0 ≤ φ < 2π.

Точкам z = r e^iφ, лежащим на листе D₀ и склейке D₀ с D_n-1, ставим в соответствие значение корня с k = 0; точкам, лежащим на листе D₁ и склейке D₁ с D₀, — значение корня с k = 1. Вообще, точкам, лежащим на D_k, при 1 ≤ k ≤ n-1, и склейке D_k, с D_k-1, соответствует значение корня с данным k. Построенное соответствие будет однозначной функцией на римановой поверхности.

Нетрудно показать, что эта функция взаимно-однозначно отображает риманову поверхность на всю комплексную плоскость. Действительно, лист D_k будет отображаться в угол, а склейки отобразятся в лучи, соединяющие эти углы; тем самым вся комплексная плоскость будет покрыта образами точек римановой поверхности.

Покажем, что это отображение является и непрерывным. Если точка z лежит на листе D_k с разрезом, то непрерывность в этой точке прямо следует из формулы (20) с фиксированным к. Для демонстрации непрерывности в точках склеек рассмотрим контур на римановой поверхности, состоящий из точек, расположенных над окружностью |z| = 1 комплексной плоскости. Начнем обходить этот контур с точки z, расположенной на верхнем крае разреза листа D₀. Так как r = 1, φ = 0, k = 0, то w = = 1. При обходе первого витка контура на листе D₀ будет

и . Перейдя по склейке на лист D₁, мы получим, по определению, (так как к = 1). В частности, при φ = 0 будет то же самое значение корня, к которому мы приближались, подходя к нижнему берегу разреза по листу D₀. Значит, в точках склейки D₀ c D­₁ функция будет непрерывной. Аналогично показывается непрерывность корня и при переходе с D_k-1 на D_k при 1 ≤ k ≤ n-1. Наконец, обходя контур по листу D_n-1 и приближаясь к нижнему краю разреза, получим k = n - 1, , и ,

т.е. то самое значение, с которого мы начинали на верхнем крае разреза листа D₀. Таким образом, функция будет непрерывной во всех точках римановой поверхности. Как функция, обратная к аналитической, она является также однозначной аналитической функцией на этой поверхности (кроме точек z = 0 и z = ∞).

Возьмем любую окружность |z| = r на комплексной плоскости, охватывающую точку z = 0. Эта окружность будет охватывать также и точку z = ∞. Обходя контур на римановой поверхности, состоящий из точек, расположенных над этой окружностью, мы будем переходить с одного листа римановой поверхности на другой. Поэтому точки z = 0 и z = ∞ называются точками ветвления. Ни одна другая точка описанным свойством не обладает: если взять окружность с центром в точке z ≠ 0, z ≠ ∞, не содержащую внутри себя точку 0, то соответствующие точки на римановой поверхности образуют n окружностей, не связанных друг с другом. Обходя каждую из них, мы не выйдем за пределы одного и того же листа.

Однозначная аналитическая в области D функция f (z) называется регулярной ветвью многозначной функции F (z), определенной в этой же области, если значение f (z) в каждой точке z области D совпадает с одним из значений F (z) в этой точке.

Многозначная функция F (z) является однозначной и аналитической на своей римановой поверхности (за исключением точек ветвления). Поэтому возможность выделить в области D регулярную ветвь означает возможность расположить эту область на римановой поверхности, не разрезая D и не задевая точек ветвления. Область D должна при этом целиком укладываться на одном листе или спускаться по склейке с одного листа на другой (как ковер по лестнице). Например, кольцо 1 < |z| < 2 нельзя без разрывов расположить на римановой поверхности функции F (z) = , n ≥ 2, поскольку точки кольца, располагаемые над положительной полуосью, должны одновременно попасть на разные листы, что невозможно. Но если разрезать кольцо по любому радиусу, то такое расположение становится возможным. При этом расположить D на римановой поверхности можно n способами (и, следовательно, выделить в D n различных ветвей функции ). Для выделения конкретной ветви достаточно указать значение функции в какой-либо точке области D. Тем самым указывается лист римановой поверхности, на который попадает эта точка, а значит, фиксируется расположение и всей области D.

4.4 Показательная и логарифмическая функции

1. Показательная функция e^z определяется следующими соотношениями: для любого комплексного числа z = х + iу

e^z = e^{x + iy} = e^x(cos y + i sin y). (21)

Второе равенство в (21) получается, если принять по определению е^{х + iу} = е^хе^iу и применить к е^iу формулу Эйлера . Из (21) следует, что

|e^z| = |е^x+iу| = е^x, Arg e^z = у + 2 πn.

Определение (21) и свойства функции е^iφ позволяют легко доказать, что функция e^z обладает обычными свойствами показательной функции:

e^z1+z2 = e^z1e^z2; e^{z1 – z2} = e^z1/e^z2; (e^z)ⁿ = e^nz.

Докажем, что функция e^z будет аналитической во всей комплексной плоскости С. Для этого надо проверить выполнимость условий Коши—Римана (7). Если w = u + iv, то в силу (21) u + iv = е^х cos у + iе^х sin у, откуда u = е^х cos у, v = e^x sin y;



Таким образом, условия (7) выполнены, и аналитичность функции e^z доказана. Чтобы вычислить производную (e^z)’, воспользуемся независимостью производной от направления и вычислим производную в направлении оси ОХ:

.

Следовательно, для производной функции e^z имеет место обычная формула

(e^z)’ = е^z .

Следующее свойство функции e^z не имеет аналога в случае показательной функции действительного переменного: функция e^z является периодической с чисто мнимым периодом 2πi. В самом деле, для любого целого n

e^{z +2πni} = e^x(cos(y + 2πn) + i sin(у+2πn)) = е^x(cos y + i sin y) = e^z.

Из периодичности функции w = e^z следует, в частности, что она не является однолистной во всей комплексной плоскости. Для выяснения, в каких областях эта функция однолистна, положим z₁ = x₁ + iy₁, z₂ = х₂ + iy₂. В силу (21), равенство e^z1 = e^z2 равносильно следующим условиям:

e^x1 = e^x2, cos y₁ = cos y₂, sin y₁ = sin y₂,

откуда следует х₁ = x₂, y₁ = y₂ + 2πn, где n — произвольное целое число, или

z₁ – z₂ = 2πni. (22)

Следовательно, для взаимной однозначности отображения w = e^z в области D необходимо и достаточно, чтобы D не содержала никакой пары точек, для которой справедливо (22). В частности, этому условию удовлетворяет любая горизонтальная полоса шириной 2π, например полосы

{z : - ∞ < х < ∞, 2πk < у < 2 π(k + 1)}, k = 0, ±1, ±2,...

Каждой такой полосе соответствует совокупность значений w = e^z = e^xe^iy = ρe^iθ для которых, в силу равенств ρ = е^х, θ = у, имеем

0 < ρ < ∞, 2πk < θ < 2π(k + 1).

Эти значения w заполняют всю комплексную плоскость переменного w с разрезом по действительной положительной полуоси. При этом прямые у = у₀ (показаны на рис. 7, а пунктиром) переходят в лучи θ = у₀ (рис. 7б), а интервалы x = x₀, 2πk< у < 2π(k + 1) (показаны сплошными линиями 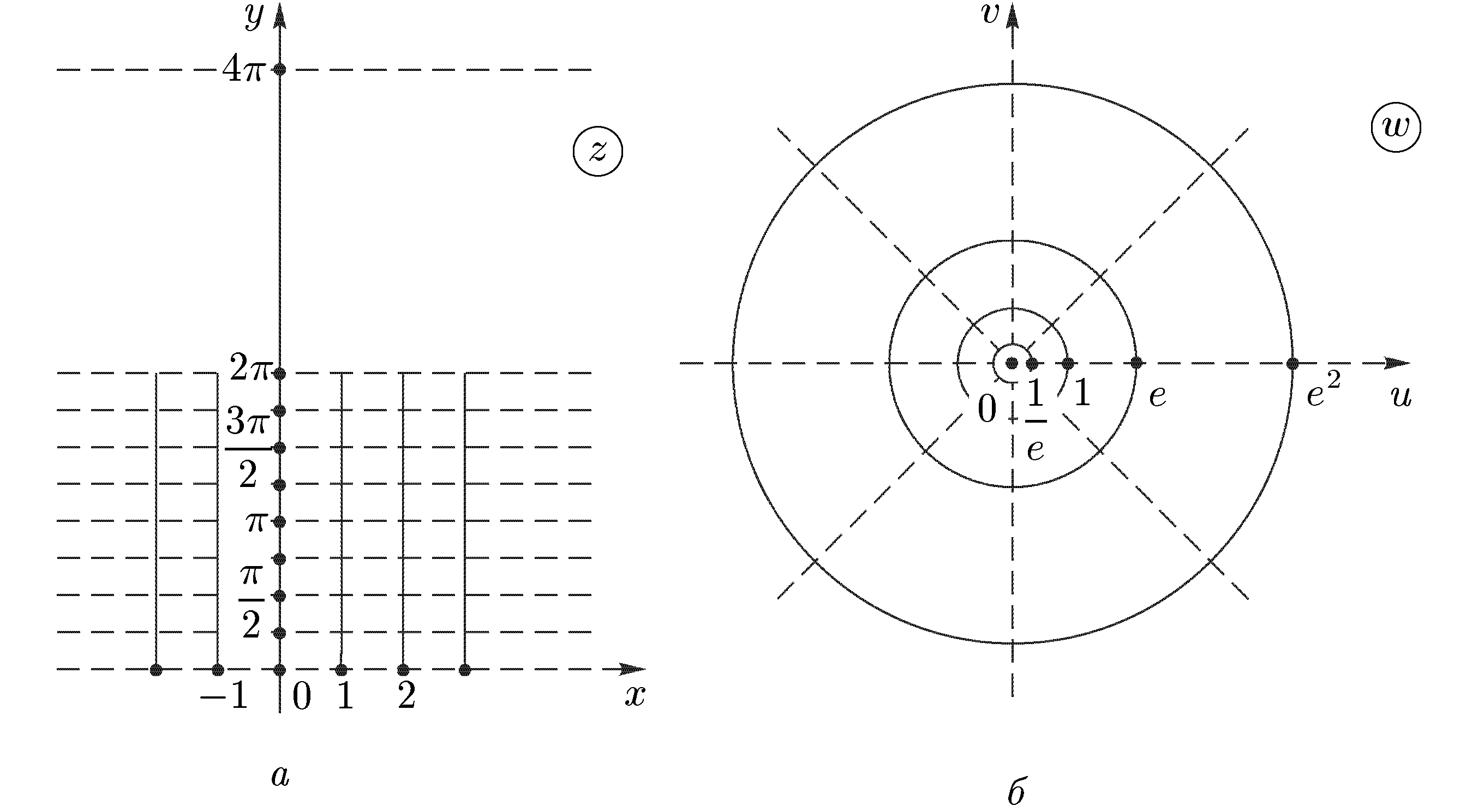(рис. 7)

для k = 0) — в окружности ρe^x0 (с выколотыми точками на полуоси u > 0). Полосы 0 < Im z < h < 2 π показательная функция e^z отображает в углы 0 < θ < h. В частности, полоса 0 < Im z < π переводится в верхнюю полуплоскость.

2. Логарифмической функцией называется функция, обратная показательной.

Так как показательная функция e^z не является однолистной в С, то обратная к ней функция будет многозначной. Эта многозначная логарифмическая функция обозначается Ln z. Таким образом, если w = Ln z, то z = e^w. Положим

w = u + iv, z = r e^iφ = re^{iArg z}.

Тогда

re^{iArg z} = z = e^w = e^{u + iv} = e^ue^iv.

Сравнивая числа, стоящие в начале и конце этой цепочки, заключаем, что

r = e^u, e ^{i Arg z} = e^iv. (23)

Из первого равенства находим u = ln r, где ln r — обычный натуральный логарифм положительного числа r. Второе равенство в (23) дает v = Arg z. Таким образом,

Lnz = ln |z| + i Arg z. (24)

Каждому комплексному числу z, отличному от 0 и ∞, формула (24) ставит в соответствие бесконечное множество значений Ln z, отличающихся друг от друга на величину 2 πki, где k — любое целое число. Удобно представить Arg z в виде

Arg z = arg z + 2 πk, - π < arg z ≤ π,

где arg z — главное значение аргумента. Тогда формула (24) примет вид

Ln z = ln |z| +i(arg z + 2πk ). (25)

Для каждого значения k функция Ln z является непрерывной однозначной функцией в комплексной плоскости с разрезом по отрицательной полуоси; она также и аналитична в этой области как функция, обратная аналитической функции e^z. Таким образом, для каждого фиксированного k формула (25) определяет регулярную ветвь многозначной функции Ln z. Эта ветвь взаимно-однозначно отображает плоскость с разрезом по отрицательной полуоси в полосу

- π + 2 πk < Im w < π + 2πk.

Ветвь, которая получается при k = 0, обозначается ln z и называется главным значением многозначной функции Ln z:

ln z = ln |z| + i arg z.

Н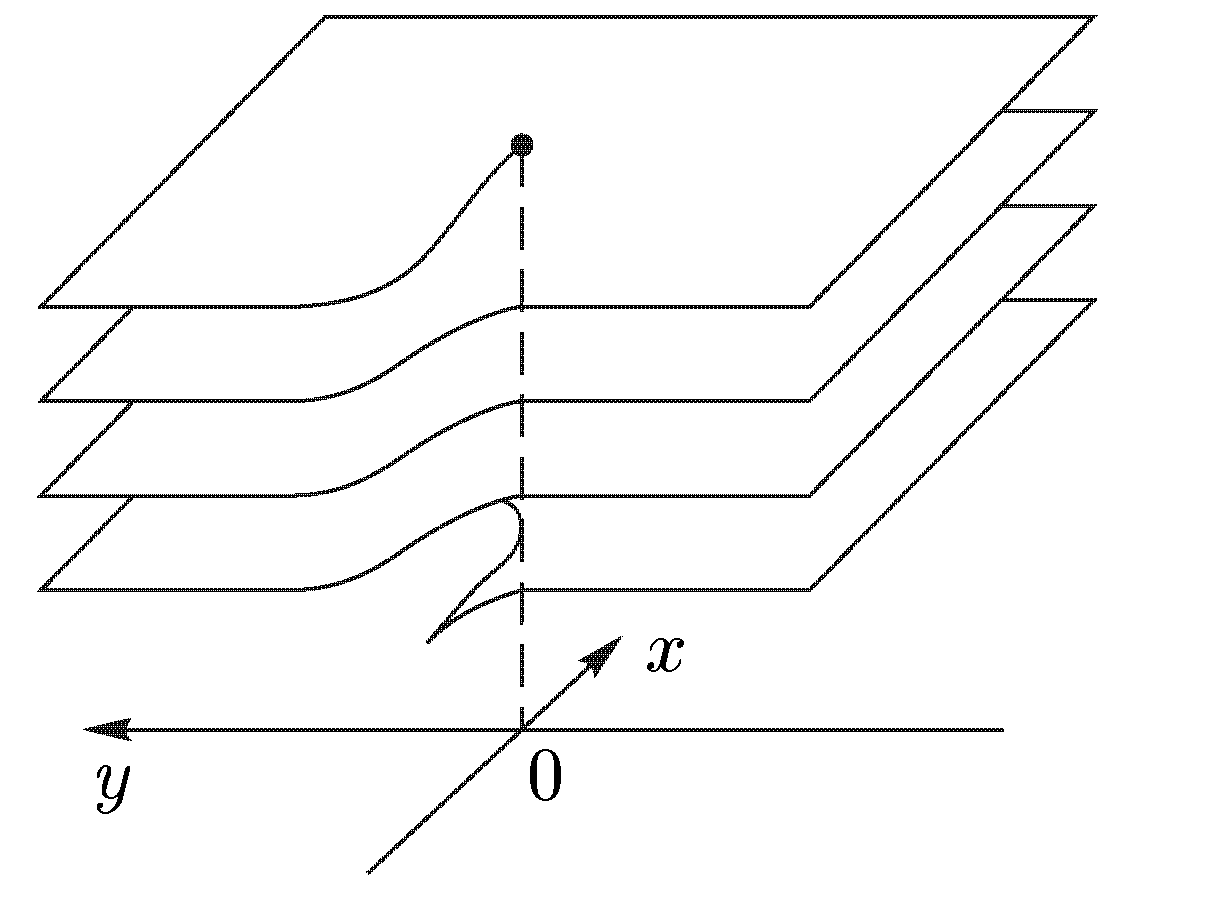апример, ln i = ln 1 + iπ/2 = iπ/2; ln(-i) = ln 1 — iπ/2 = —iπ/2. Если приближаться к точке z = — 1 по верхней полуплоскости у > 0, то ; если по нижней, — то .

Чтобы представить себе риманову поверхность функции Ln z, возьмем бесконечное количество экземпляров ("листов") плоскости с разрезом по отрицательной полуоси и склеим их так, как показано на рис. 8. Над каждой точкой плоскости, кроме точек z = 0 и z = ∞,

располагается бесконечно много точек (рис. 8)

римановой поверхности. В точках 0 и ∞ функция Ln z не определена, и точек поверхности над ними нет. Точки z = 0 и z = ∞ называются точками ветвления бесконечного порядка.

Рис. 8 наглядно демонстрирует причину того, что : если предположить, что точки — 1 ± h, h > 0, находятся на одном и том же листе римановой поверхности и устремить h, к нулю, то предельные положения этих точек окажутся на разных листах римановой поверхности.

Выделить регулярную ветвь логарифма можно не только в области D, являющейся плоскостью с разрезом по отрицательной полуоси. Если сделать разрез плоскости по любому лучу, то полученная область также допускает выделение в ней регулярной ветви. Пусть разрез сделан по лучу, идущему под углом θ к оси ОХ. Тогда регулярные ветви будут задаваться следующей формулой: при z = e^iφ

Ln z = ln r + i(φ + 2πk), θ < φ < θ + 2 π.

Формула (25) является частным случаем при θ = - π. Производная каждой регулярной ветви f (z) логарифма находится по формуле , аналогичной формуле для производной логарифмической функции действительного переменного. Этот факт выводится из равенства (e^z)’ = e^z и формулы (19) производной обратной функции. Действительно, обратной к w = f(z) будет функция z = e^w. Отсюда и из (19) получаем

.

4.5 Общая степенная и тригонометрические функции. Функция Жуковского

1. Общая степенная функция , где — фиксированное комплексное число, определяется соотношением .

Полагая , получаем Ln z = ln r + i(φ + 2πk). Следовательно, .

Отсюда видно, что при модуль принимает бесконечное множество значений. Таким образом, при функция будет бесконечнозначной.

Общая степенная функция в силу своего определения допускает выделение регулярных ветвей в тех же областях, что и логарифмическая; например в плоскости с разрезом по лучу. Ветвь , выделенная в плоскости с разрезом вдоль отрицательной полуоси, называется главной ветвью степенной функции. В силу теоремы о производной сложной функции для каждой регулярной ветви степенной функции справедливы равенства ,

где f (z) — регулярная ветвь логарифмической функции Ln z. Мы получили обычную формулу для производной степенной функции:

.

2. Перейдем к тригонометрическим функциям. Для действительных значений х из формулы Эйлера следует, что

е^iх = cos х + i sin x, е^{- iх} = cos x — i sin x.

Отсюда cos x = , sin x =. Эти формулы служат основой следующего определения.

Тригонометрические функции комплексного переменного z определяются равенствами

,,,.(26) Определенные таким образом функции сохраняют многие свойства тригонометрических функций действительного переменного. Из периодичности функции e^z следует, что функции sin z и cos z периодичны с периодом 2 π, a tg z и ctg z — с периодом π. Функция sin z нечетна, a cos z — четна. Действительно, . Аналогично доказывается четность функции cos z. Для функций, определенных равенствами (26), справедливы обычные тригонометрические соотношения. Например,

sin² z + cos² z = 1, sin(z₁ + z₂) = sin z₁ cos z₂ + cos z₁ sin z₂ и т.д. Все эти соотношения вытекают из (26).

Функции sin z и cos z аналитичны во всей плоскости С, причем имеют место обычные формулы дифференцирования:

(sin z) ' = cos z, (cos z) ' = - sin z.

Докажем, например, формулу для производной sinz: Используя формулы для производной частного, получим

,.

Однако не все свойства тригонометрических функций действительного переменного сохраняются при продолжении этих функций в комплексную плоскость. В частности, sinz и cosz могут принимать значения, по модулю превосходящие 1. Например,

;.

3. Функции, обратные (26), называются обратными тригонометрическими функциями. Так как тригонометрические функции (26) периодичны, то обратные к ним функции будут бесконечнозначными. В силу того что функции (26) достаточно просто выражаются через показательные, обратные к ним функции удается выразить через логарифмы. Получим такое выражение, например, для w = Arccos z. Из определения этой функции имеем

z = cos w = , откуда e^{2 iw} — 2ze ^iw + 1 = 0. Решая это квадратное уравнение относительно e ^iw, находим (мы опускаем ± перед знаком квадратного корня, поскольку понимаем корень как двузначную функцию, принимающую оба соответствующих значения). Из последнего равенства получаем

.

В силу соотношения изменение знака перед корнем приводит к изменению знака перед логарифмом. Но корень принимает значения как с "+" так и с "—". Значит, и среди значений Arccos z будут значения как с "+", так и с " —" перед логарифмом. Поэтому знак "—" можно не писать:

(27)

Аналогичные формулы можно дать и для других обратных тригонометрических функций:



(28)

Из элементарных функций комплексного переменного отметим также гиперболические функции sh z, ch z, th z, и cth z, определяемые равенствами

,,

,, (29)

Они весьма просто выражаются через тригонометрические функции:

sh z = — i sin iz, ch z = cos iz, th z = — i tg iz, cth z = i ctg iz,

и поэтому несущественно отличаются от последних.

4. Функцией Жуковского называется функция

. (30)

Эта функция имеет важные применения в теории крыла самолета, а также весьма полезна при построении ряда конформных отображений. Она аналитична всюду в , кроме точек z = 0 и z = ∞. Производная



существует всюду в , за исключением точек z = 0 и z = ∞, и обращается в нуль при z = ±1. Поэтому отображение (30) конформно всюду, кроме точек 0, ±1 ,∞.

Выясним, при каком условии две различные точки переходят в одну и ту же точку. Пусть z₁ ≠ z₂ и .

Отсюда следует, что .

Так как z₁ ≠ z₂, то это равенство равносильно условию z_lz₂ = 1. (31)

Поэтому для однолистности функции Жуковского в некоторой области D необходимо и достаточно, чтобы эта область не содержала пары различных точек, удовлетворяющих условию (31). Такими областями являются, например, внешность |z| > 1 единичного круга (при этом |z₁z₂| > 1) и внутренность |z| < 1 этого круга (|z₁z₂| < 1).

Чтобы наглядно представить себе отображение (30), выясним, в какие кривые оно переводит окружности (показаны на рис. 9а сплошными линиями) и лучи (показаны пунктирами). Положим z =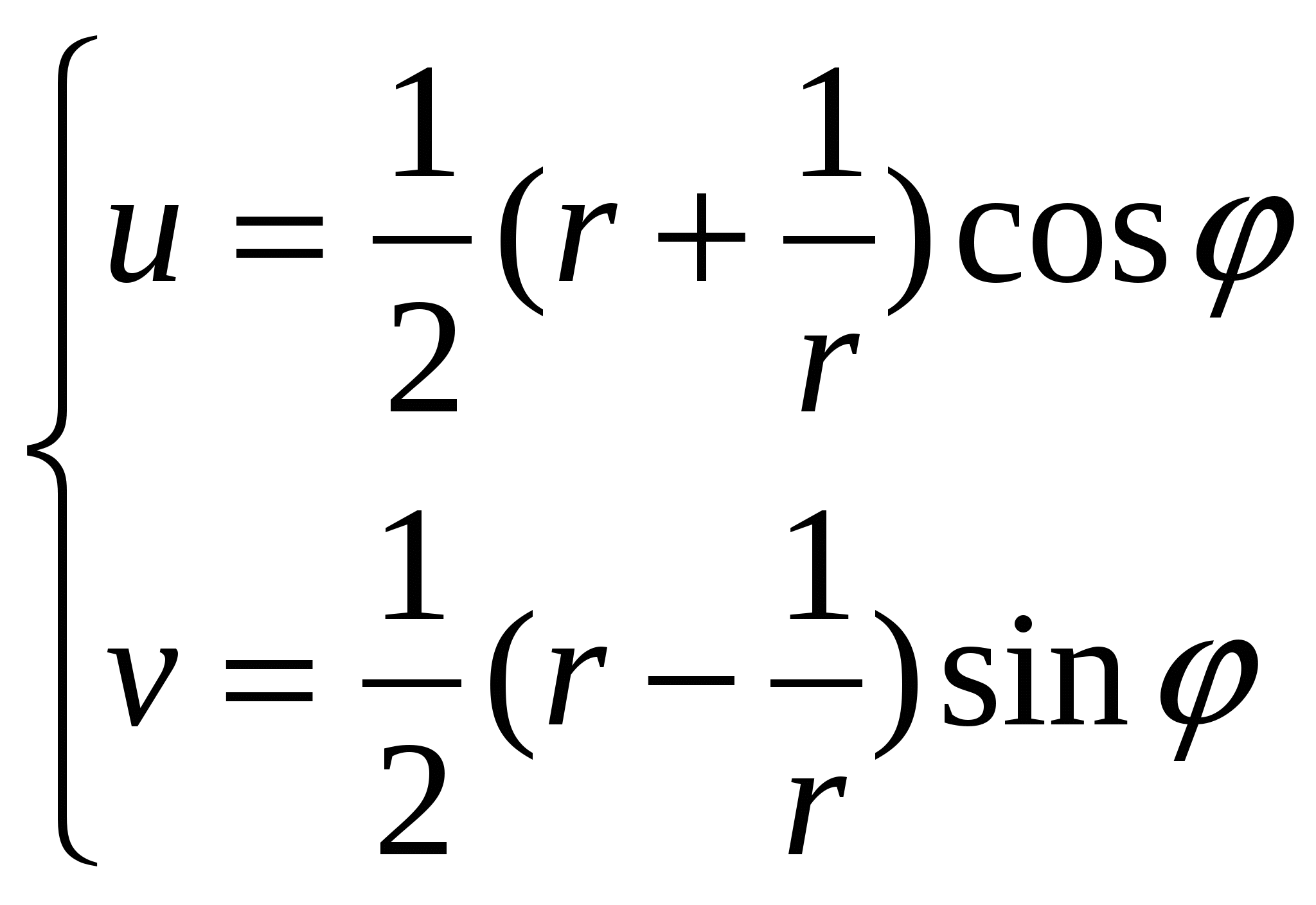. Тогда (30) перепишется в виде , откуда (32)

Рассмотрим образы окружностей r = r₀. Из (32) следует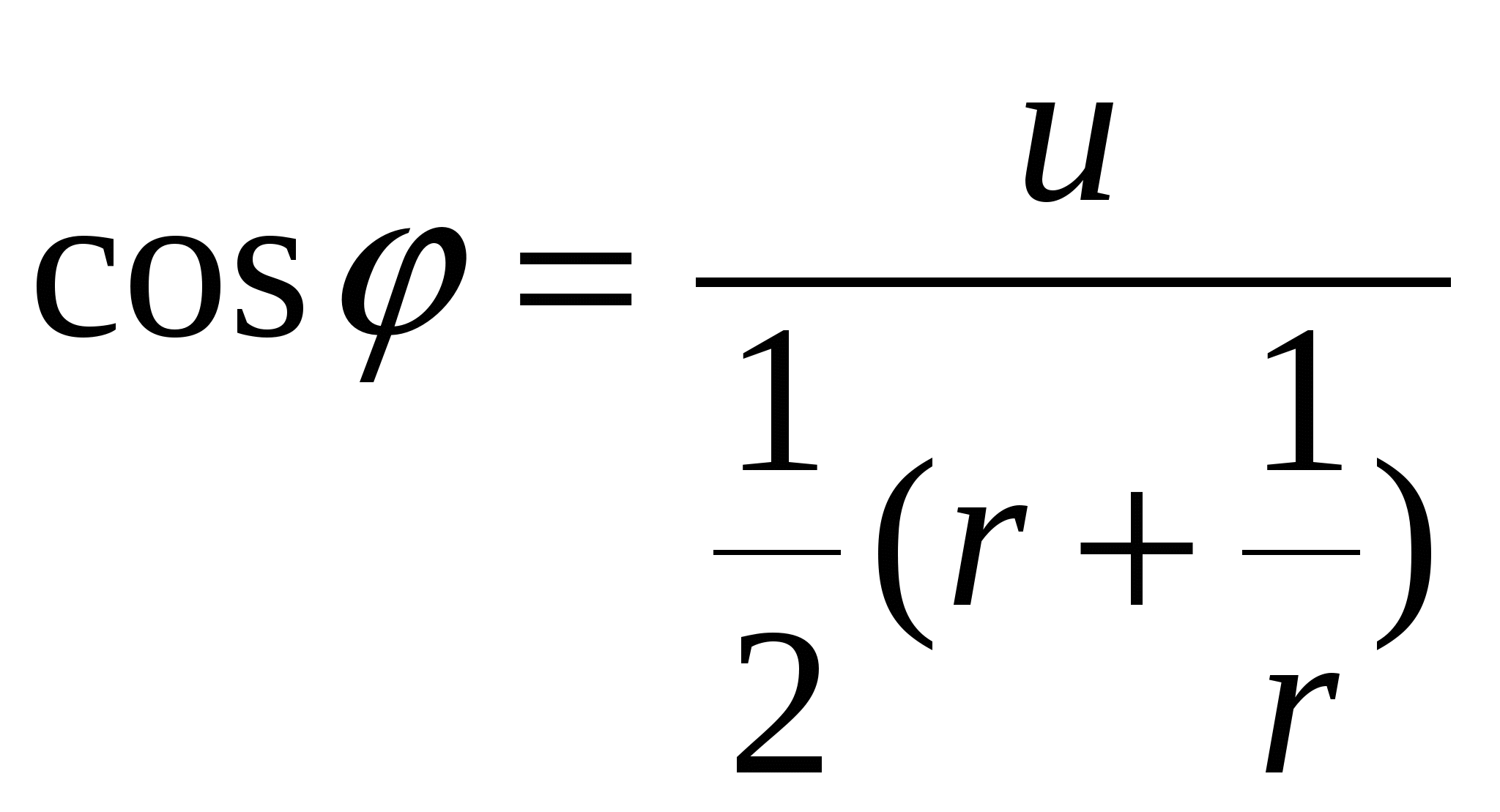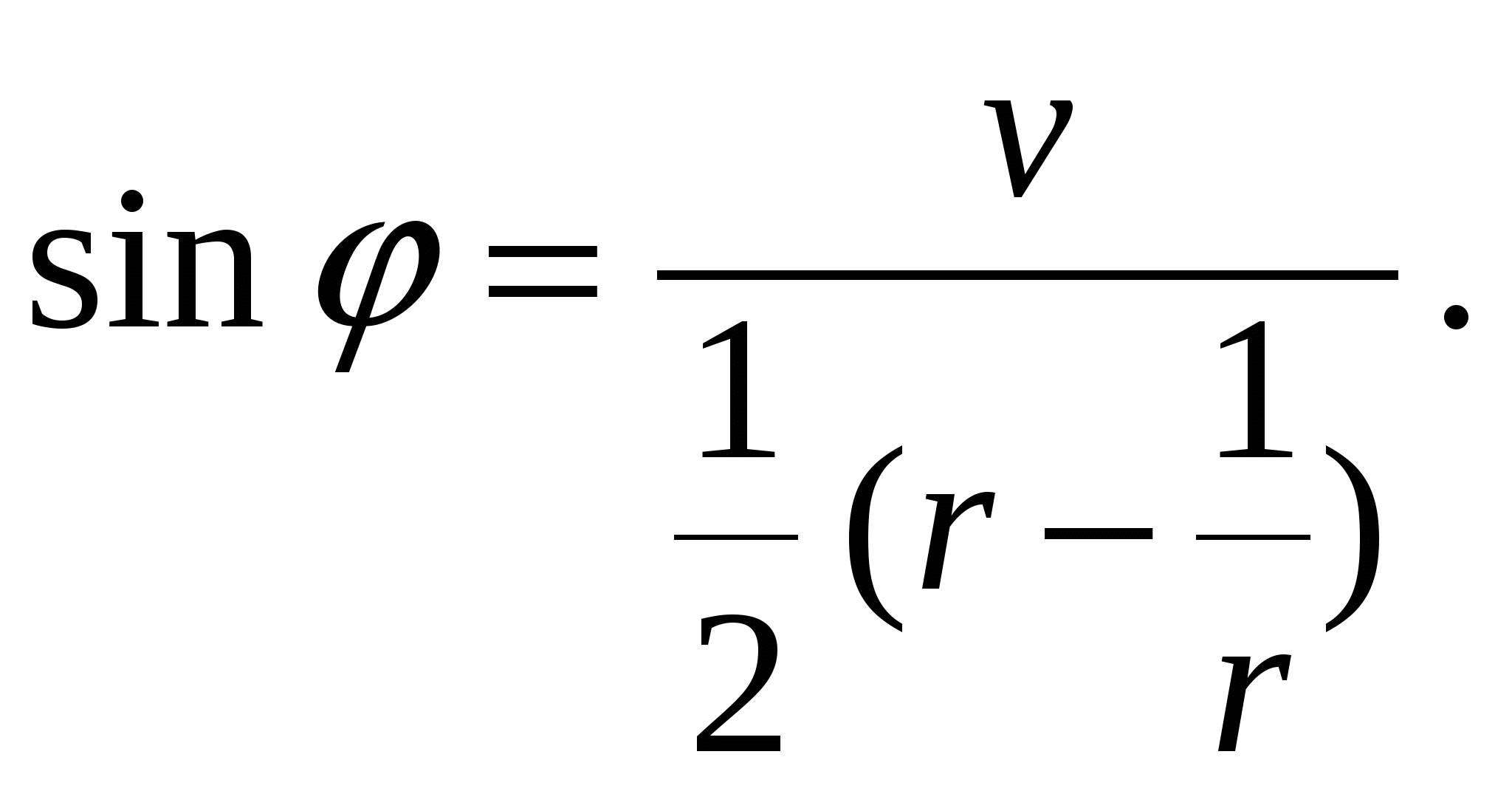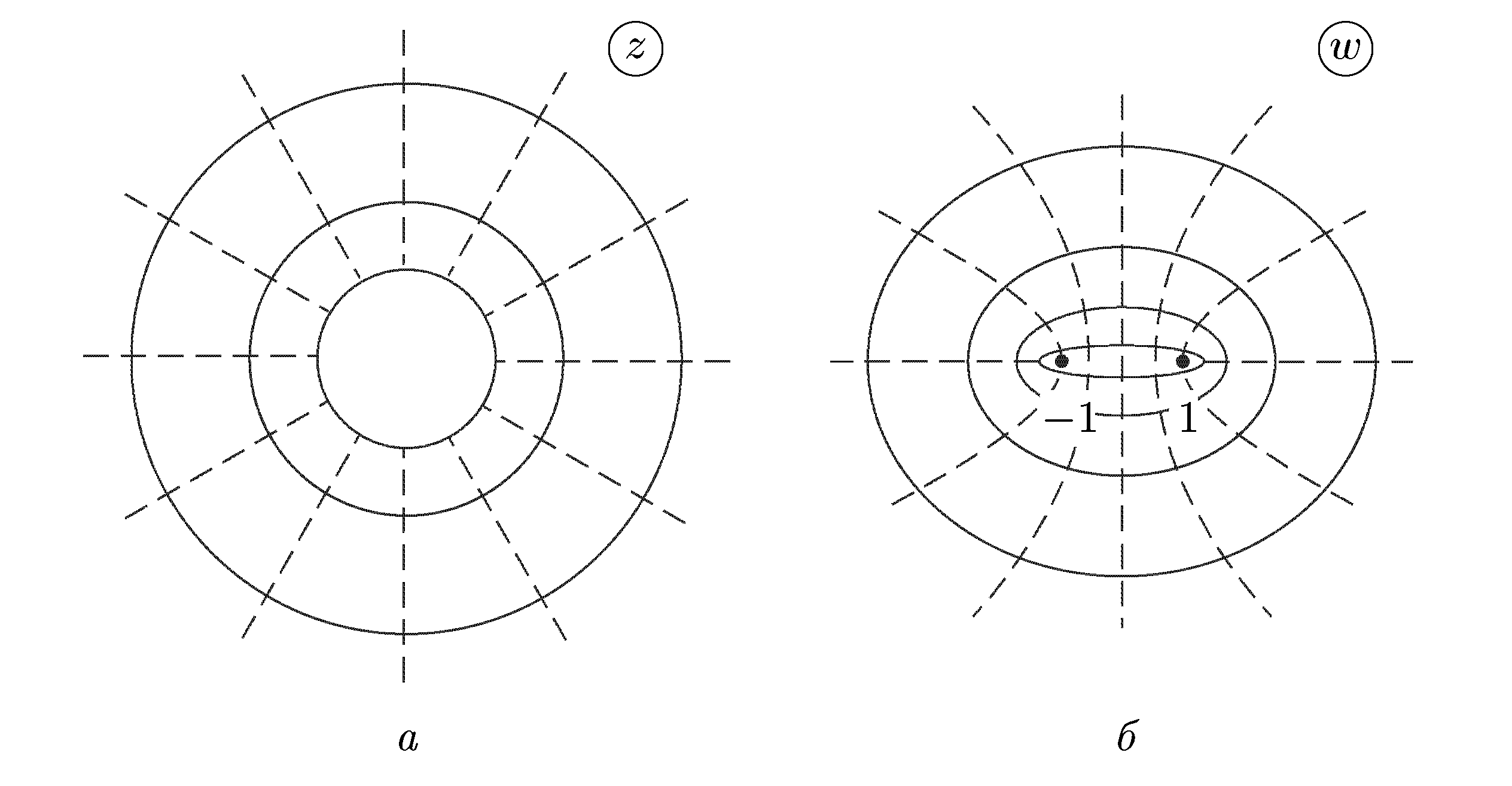

,

(рис. 9)

Возводя эти равенства в квадрат, складывая и полагая r = r₀, получим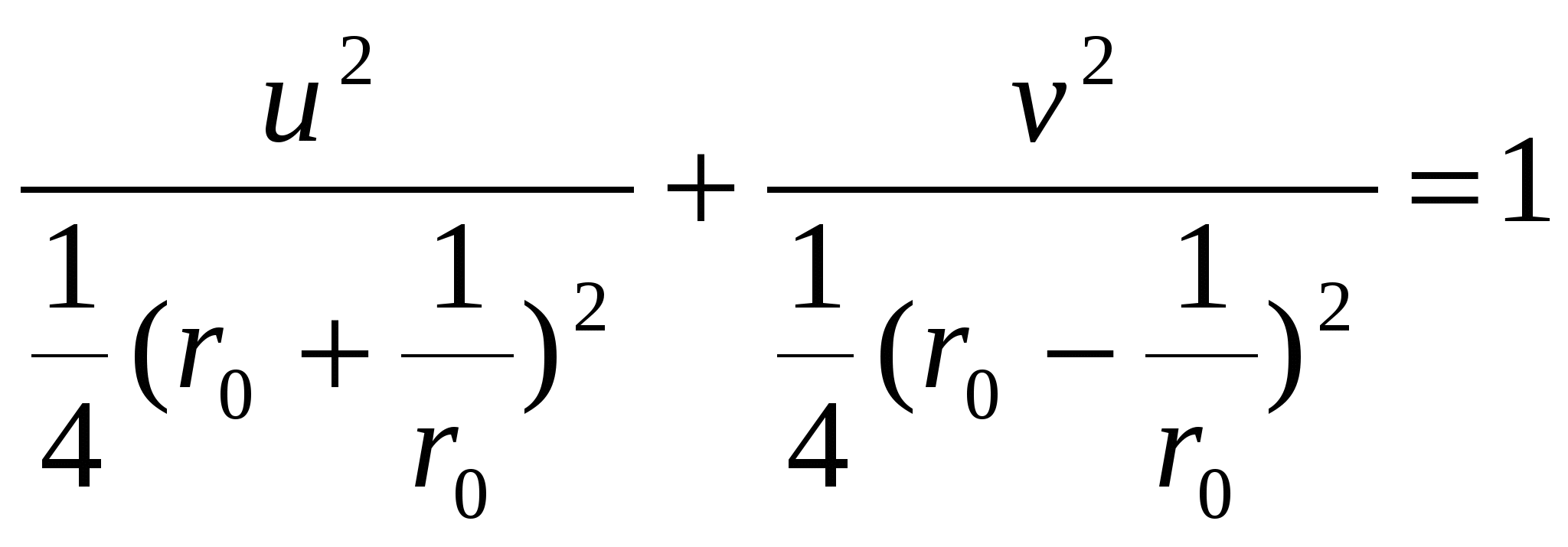

(33)

Уравнение (33) является уравнением эллипса с полуосями



Итак, образами окружностей |z| = r₀ в плоскости z будут эллипсы в плоскости w (рис. 9б). Если r₀ → 1, то a _{r 0} → 1, b _{r 0} → 0. Поэтому эллипсы будут стягиваться к отрезку [—1,1]. При больших r₀ разность a _{r 0} — b _{r 0} = мала, и эллипсы мало отличаются от окружностей.

Чтобы получить образ лучей , преобразуем равенства (32) к виду



Возводя эти равенства в квадрат, вычитая из первого второе и полагая , получим (34)

Уравнение (34) является уравнением гиперболы с полуосями ,. Следовательно, лучи отображаются в части гипербол (рис. 9б).

Таким образом, функция Жуковского взаимно-однозначно и конформно отображает внешность единичного круга на внешность отрезка [-1,1].

Из (30) легко видеть, что w(z) = w(l/z). Функция w = 1/z взаимно-однозначно и конформно отображает внутренность круга |z| < 1 на внешность этого же круга. Отсюда следует, что функция Жуковского взаимно-однозначно и конформно отображает также и внутренность единичного круга на внешность отрезка [—1,1].

Список литературы.

1. Эйдерман В. Я. «Основы теории функций комплексного переменного и операционного исчисления.»

2. Свешников А. Г., Тихонов А. Н. «Теория функций комплексной переменной»