реферат по тфкп. Реферат по теме Конформные отображения

• Название: Реферат по теме Конформные отображения
• Анкор: реферат по тфкп.doc
• Дата: 03.05.2018
• Размер: 0.66 Mb.
• Имя файла: реферат по тфкп.doc
• Тип: Реферат; #18852
• страница: 2 из 3

Свойство 1. (принцип сохранения области). Если функция w = f(z) аналитична в области D и отлична от постоянной, то множество D', на которое она отображает D, также является областью (т.е. открытым связным множеством).

Перейдем к утверждениям, описывающим соответствие границ при конформных отображениях.

Свойство 2. (принцип соответствия границ). Пусть D и D' — односвязные области, ограниченные непрерывными замкнутыми контурами Г и Г’, составленными из конечного числа гладких кривых. Пусть, далее, функция w = f(z) конформно отображает D на D'. Тогда эту функцию можно доопределить и в точках границы Г так, что она станет непрерывной в замкнутой области и отобразит Г взаимно-однозначно и непрерывно на Г '.

Указанное свойство означает, что при конформном отображении друг на друга двух областей между их границами устанавливается взаимно-однозначное и непрерывное соответствие.

Свойство 3. При взаимно-однозначном и конформном отображении областей D и D' сохраняется направление обхода их границ.

Другими словами, если при обходе границы область D остается слева, то и при соответствующем обходе границы области D' эта область остается слева.

Большое значение для построения конформных отображений имеет следующее свойство.

Свойство 4. (обратный принцип соответствия границ).

Пусть односвязные области D и D' ограничены кривыми Г и Г’. Пусть, далее, функция w = f(z), аналитическая в D и непрерывная в , отображает Г взаимно-однозначно на Г ', причем, когда точка z обходит контур Г так, что область D остается слева, соответствующая точка w обходит контур Г ' так, что область D' также остается слева. Тогда функция w = f(z) осуществляет взаимно-однозначное конформное отображение области D на область D'.

Следовательно, для отыскания области, на которую функция w = f(z) отображает заданную область D, достаточно обойти границу области D и найти контур, на который эта граница отображается функцией f(z).

4. Основные функции.

4.1 Линейная функция.

Функция w = az + b, (10) , где а и b — заданные комплексные числа и а≠0, называется линейной функцией. Так как w ’ = а ≠ 0, то отображение (10) является конформным во всей плоскости С. Докажем, что оно также однолистно в С. Если w₁ = az₁ + b, w₂ = az₂ + b, то w₁ — w₂ = a(z₁ — z₂). Поэтому при z₁ ≠ z₂ получаем, что w₁ ≠ w₂ , и однолистность установлена. Положив по определению w(∞) = ∞, получим однолистное отображение всей расширенной комплексной плоскости на .

Для изучения геометрических свойств отображения (10) рассмотрим вначале случай b = 0, т.е. w = az. Пусть а = , z = .Тогда

w = .

Поэтому для получения вектора w = az нужно выполнить следующие два действия:

1) умножить заданный вектор z на |а|. При этом направление вектора z останется прежним, но длина увеличится в |а| раз. Значит, умножение на |а| есть преобразование подобия (гомотетия) с центром в начале координат и коэффициентом подобия |а|;

2) повернуть полученный вектор |a|z на угол α.

Для рассмотрения общего случая (10) заметим, что при сложении вектора az с вектором b происходит параллельный перенос концевой точки вектора az на вектор b. Итак, отображение (10) получается путем композиции (т.е. последовательного выполнения) следующих трех операций: 1) преобразования подобия с центром в начале координат и коэффициентом подобия |а|; 2) поворота вокруг начала координат на угол α; 3) параллельного переноса на вектор b.

4.2 Дробно-линейная функция.

Перейдем к изучению дробно-линейной функции, определяемой равенством

, (11)

и соответствующего дробно-линейного отображения. Так как

, ,

то естественно определить w(∞) = а/с, w(—d/c) = ∞. Определенная таким образом функция будет непрерывной во всей расширенной комплексной плоскости .

Если с = 0, то w = и дробно-линейная функция сводится к уже изученной линейной функции. Поэтому в дальнейшем предполагается, что с ≠ 0.

Умножим числитель и знаменатель дроби (11) на с и добавим в числителе +ad — ad. Тогда дробь (11) можно представить в виде

. (12)

Если bc — ad = 0, то w = a/c и функция (11) сводится к постоянной. В дальнейшем считаем выполненными условия

с ≠ 0, bc – ad ≠ 0. (13)

Покажем, что дробно-линейная функция (11) осуществляет взаимно-однозначное отображение на . С этой целью решим уравнение (11) относительно z (это возможно при z ≠ —d/c, z ≠ ∞, w ≠ а /с, w ≠ ∞):

.

Поэтому каждое значение w ≠ а/с и w ≠ ∞ имеет только один прообраз z ≠ - d/c и z ≠ ∞. Но в силу определения значению w = а/с соответствует z = ∞, а значению w = ∞ — величина z = —d/c. Итак, каждая точка w имеет только один прообраз z , что и требовалось доказать.

Установим теперь конформность отображения (11). Так как

,

то при z ≠ - d/c и z ≠ ∞ производная w' существует и не равна нулю. По теореме 1 дробно-линейное отображение является конформным всюду, кроме этих двух точек.

Для выяснения конформности при z = - d/c и z = ∞ нам понадобится следующее определение.

Под углом между двумя линиями в точке z = ∞ понимается угол между образами этих линий при отображении w = в начале координат.

Теорема 5. Дробно-линейная функция

, ad — bс ≠ 0, w(∞) = а/с, w(- d/c) = ∞, (14)

осуществляет взаимно-однозначное и конформное отображение расширенной комплексной плоскости на всю .

Мы не исключаем случай с = 0 в теореме 5, так как в этом случае дробно-линейная функция становится линейной, также обладающей всеми свойствами, указанными в теореме 5.

Установим теперь круговое свойство дробно-линейного отображения. Для единообразия дальнейших формулировок удобно рассматривать прямую как окружность бесконечно большого радиуса.

Теорема 6. При дробно-линейном отображении (14) окружности всегда переходят в окружности.

(Заметим, что окружность конечного радиуса может переходить в окружность бесконечного радиуса, т.е. в прямую, и наоборот.)

Доказательство. Рассмотрим уравнение

А(х² +у²) + Вх + Су + D = 0, (15)

где А, В, С, D — действительные коэффициенты. При А = 0 получаем Вх + Су + D = 0, т.е. уравнение прямой. Если А ≠ 0, то, разделив на А и выделив полные квадраты, придем к равенству

(x - x₀)² + (y - y₀)² = ± R²

которое определяет либо окружность, если справа +R², либо точку, если R = 0, либо пустое множество, если справа –R². С другой стороны, любую окружность (в частности, прямую) можно задать уравнением вида (15).

Докажем вначале круговое свойство для отображения w = 1/z. Возьмем произвольную окружность на комплексной плоскости. Она задается уравнением (15). Обозначим z = х + iy, w = u + iv. Равенство w = 1/z дает z = 1/w, или

,

откуда

, .

Чтобы получить уравнение кривой, в которую перейдет окружность при отображении w = 1/z, подставим в (15) найденные выражения для х и у:



или

A + B u – C v + D (u² + v²) = 0

Мы пришли к уравнению такого же вида, что и (15), но в плоскости переменного w = u + iv. Как мы видели ранее, такое уравнение определяет либо окружность (в частности, прямую при D = 0), либо точку, либо пустое множество. Но в силу взаимной однозначности дробно-линейного отображения окружность не может перейти в точку или в пустое множество. Значит, она переходит в окружность и круговое свойство отображения w = 1/z установлено.

Рассмотрим теперь общий случай дробно-линейного отображения (14). Если с = 0, то получим линейное отображение w = a₁z + b₁, которое сводится к растяжению с поворотом и сдвигу. Каждое из этих преобразований, очевидно, обладает круговым свойством. Значит, и для отображения w = a₁z + b₁ данное свойство имеет место.

Пусть теперь с ≠ 0. Воспользовавшись равенством (12), представим дробно-линейное отображение в виде

, (16)

где Е = , F =, G =.

Из равенства (16) следует, что дробно-линейное отображение представлено в виде композиции следующих трех преобразований:

1) w₁ = z + G; 2) w₂ = 1/w; 3) w = E + Fw₂. Как было установлено выше, каждое из этих преобразований окружность переводит в окружность. Значит, их композиция также обладает этим свойством, что и требовалось доказать.

Чтобы сформулировать еще одно свойство дробно-линейных отображений, нам понадобиться следующее определение.

Точки А и А' называются симметричными относительно окружности радиуса R < ∞, если они лежат на одном луче, выходящем из центра О окружности, и

О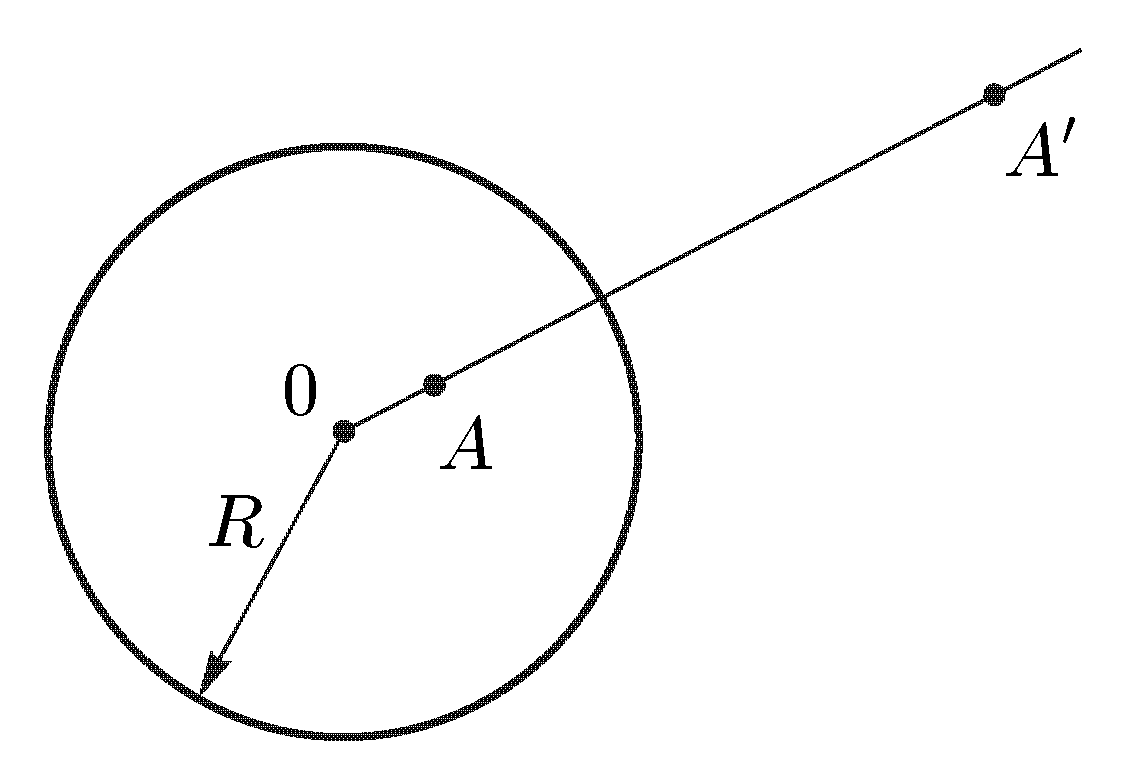А• ОА' = R². (17)

Если точка А приближается к окружности (см. рис. 4), т.е. если ОА → R, то О А' тоже стремится к R; всякая точка на окружности симметрична самой себе; если ОА → 0, то ОА' → ∞. Поэтому для точки О симметричной будет бесконечно удаленная точка. Под симметрией относительно

окружности радиуса R = ∞ понимается (рис. 4) обычная симметрия относительно прямой.

Лемма 7. Для того чтобы точки А и А' были симметричными относительно окружности Г (возможно, бесконечного радиуса), необходимо и достаточно, чтобы любая окружность, проходящая через А и А', была перпендикулярна Г (рис. 5).

Д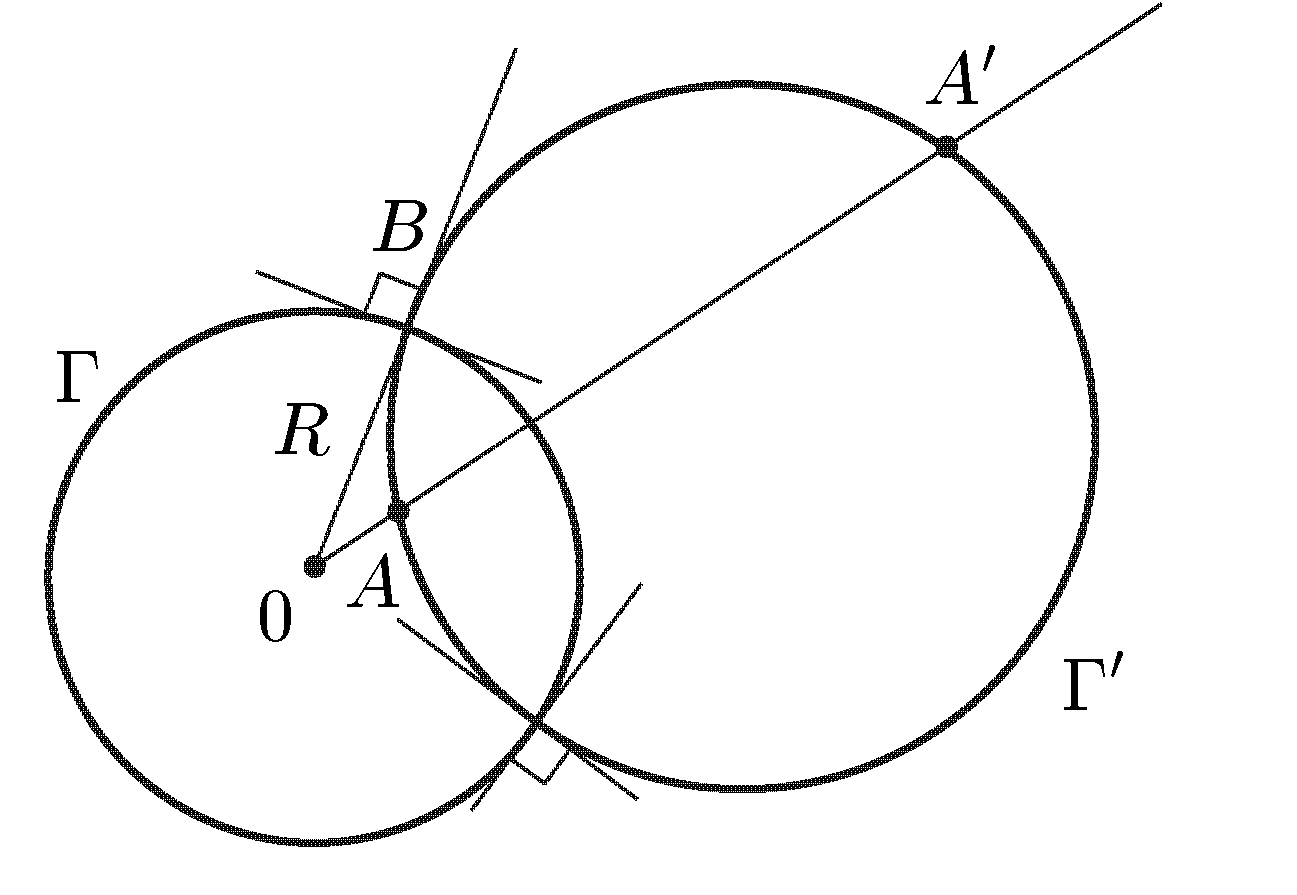оказательство. Необходимость. Пусть точки А и А' симметричны относительно окружности Г. Проведем произвольную окружность Г ' через точки А и А’ , и пусть В — точка пересечения окружностей Г и Г’. По известной теореме о секущей и касательной произведение секущей ОА' на ее внешнюю часть ОА равно квадрату касательной. В то же время, в силу

симметрии, ОА • ОА’ = R². Значит, (рис. 5)

радиус ОВ является касательной к окружности Г’. Поскольку радиус ОВ перпендикулярен касательной к Г, проходящей через точку В, то окружности Г и Г’ перпендикулярны, что и требовалось доказать. Если Г' — прямая (это будет в случае А = 0), то она проходит через точку О и, следовательно, также перпендикулярна Г.

Достаточность. Пусть точки А и А' таковы, что любая окружность (в частности, прямая), проходящая через них, пересекает Г под прямым углом (см. рис. 5). Докажем, что А и А’ симметричны относительно Г. Так как прямая АА' перпендикулярна Г, то она проходит через точку О. Значит, точки О, А, А' лежат на одной прямой. Но они лежат и на одном луче, выходящем из точки О. Действительно, если бы точки А и А' лежали по разные стороны от точки О, то окружность с диаметром АА' не была бы перпендикулярна Г.

Проведем произвольную окружность Г ' через А и А' с радиусом R’ < ∞. Пусть В — точка пересечения Г и Г’. По условию, Г и Г’ пересекаются под прямым углом. Поэтому радиус ОВ будет касаться Г '. По той же теореме о секущей и касательной ОА • ОА' = R². Следовательно, точки А и А' симметричны относительно Г.

Мы доказали лемму 7 в случае R < ∞. Если R = ∞, то рассуждение существенно упрощается.

Теперь мы готовы установить следующее свойство дробно-линейных отображений (свойство сохранения симметрии):

Теорема 8. При дробно-линейном отображении (14) пара точек, симметричных относительно окружности (в частности, прямой), переходит в пару точек, симметричных относительно образа этой окружности.

Доказательство. Пусть точки z₁ и z₂ симметричны относительно окружности Г. При дробно-линейном отображении (14) Г перейдет в кривую γ, которая по теореме 6 также является окружностью; точки z₁ и z₂ перейдут в точки w₁ и w₂. Надо доказать, что w₁ и w₂ симметричны относительно γ. Возьмем любую окружность γ ', проходящую через w₁ и w₂,и рассмотрим ее прообраз Г ' при отображении (14) (т.е. множество точек на плоскости переменного z, переходящих в γ '). Для этого выразим z из уравнения (14):

при ad – bc ≠ 0

Мы видим, что Г ’ получается из γ’ также дробно-линейным отображением. Поскольку γ ‘ является окружностью, то по теореме 6 Г ‘ — тоже окружность. Так как Г ‘ проходит через точки z₁ и z₂, симметричные относительно Г, то по лемме 7 окружность Г ‘ перпендикулярна Г. В силу конформности дробно-линейного отображения и γ ‘ перпендикулярна γ. По лемме 7 отсюда следует, что точки w₁ и w₂ симметричны относительно γ, и доказательство завершено.

Установленные свойства дробно-линейных отображений позволяют находить отображения областей, ограниченных окружностями (в частности, прямыми).

4.3 Степенная функция. Понятие римановой поверхности.

Рассмотрим степенную функцию

w = zⁿ, (18)

где n — натуральное число. Производная w' = nz^n-1 существует и отлична от нуля во всех точках z ≠ 0, z ≠ ∞. Поэтому отображение, осуществляемое функцией (18), является конформным во всех точках, кроме z = 0 и z = ∞. Если записать переменные z и w в показательной форме, z = r e^iφ, w = ρе^iθ, то (18) приводит к равенствам ρ = r ⁿ, θ = nφ.

Отсюда видно, что окружности |z| = r переходят в окружности |w| = r ⁿ, угол 0 < φ < α, где α < 2 π /n, с вершиной в начале координат, лежащий в плоскости переменного z, отображается на угол 0 < θ < nα плоскости w. Следовательно, конформность отображения нарушается в точке z = 0: углы в этой точке увеличиваются при отображении в n раз. Нетрудно показать, что отображение (18) не является конформным и в точке z = ∞.

Пусть точки z₁ и z₂ таковы, что z₂ = z₁ e^{i2 π /n}, n ≥ 2. Легко видеть, что z₁ ≠ z₂ , и . Поэтому отображение (18) не является однолистным во всей комплексной плоскости С, но является таковым внутри любого угла величиной α < 2 π /n с вершиной в начале координат.

Чтобы ввести функцию, обратную степенной, нам нужны следующие определения.

Многозначной функцией комплексного переменного называется правило (закон), по которому комплексному числу z из множества D соответствует несколько (возможно, бесконечно много) комплексных чисел w.

Все функции, рассмотренные ранее (кроме функции Arg z), были однозначными. Функция Arg z является многозначной:

Arg z = arg z + 2πk ,

где arg z — главное значение аргумента и к — любое целое число. В дальнейшем под термином функция, используемым без каких-либо пояснений, подразумевается однозначная функция; многозначность изучаемых функций всегда будет оговариваться дополнительно.

Пусть функция w = f(z) отображает область D на область Е. Обратной к функции w = f(z) называется функция (вообще говоря, многозначная) z = g(w), определенная на области Е, которая каждому комплексному числу w Е ставит в соответствие все комплексные числа zD, такие что f(z) = w.

Другими словами, функция, обратная к w = f(z), — это правило, по которому каждой точке wЕ соответствуют все ее прообразы zD.

Если функция w = f(z) однолистна в D, то обратная функция однозначна (и также однолистна) в Е; если w = f(z) не однолистна, то обратная функция будет многозначной. Например, обратной к функции w = zⁿ является многозначная функция z = : каждому значению w, отличному от 0 и ∞, соответствует n различных корней n-й степени, определяемых формулой

(*).

Числа 0 и ∞ имеют по одному корню: , а.