Доклад по алгебре на тему. Влияние коэффициентов на расположение графика линейной функции
 Скачать 317.39 Kb. Скачать 317.39 Kb.
|
|
Доклад по алгебре на тему: «ВЛИЯНИЕ КОЭФФИЦИЕНТОВ НА РАСПОЛОЖЕНИЕ ГРАФИКА ЛИНЕЙНОЙ ФУНКЦИИ» Линейной функцией называется функция вида y = kx + b, где х - независимая переменная, а k и b – некоторые числа. Графиком линейной функции является прямая Влияние изменения коэффициента b на изменение расположения графика. Рассмотрим графики функций y = 3x + b. Все графики проходят через точку (0; b). Пусть b ≠0 и b = -5; 1; 5, то есть будем увеличивать коэффициент b. 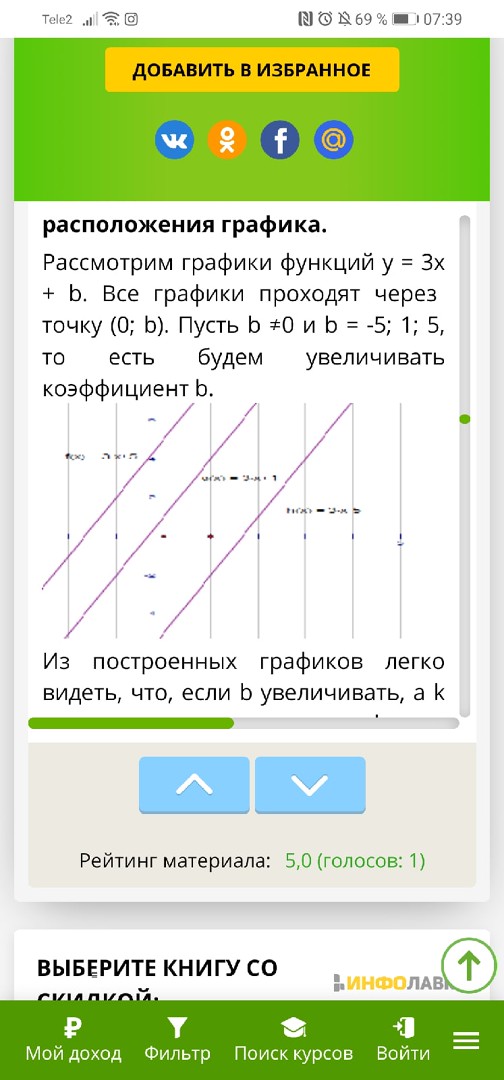 Из построенных графиков легко видеть, что, если b увеличивать, а k оставлять постоянным, то график y = kx + b смещается вверх вдоль оси Оy. Кроме того, все прямые на данном чертеже - параллельны. Рассмотрим графики функций y = - 3x + b. Пусть b ≠0 и b = 5; 1; -5, то есть будем уменьшать коэффициент b.  Видим, что, если b уменьшать, а k оставлять постоянным, то график функции y = kx + b смещается вниз вдоль оси Оy. И, ещё, прямые снова параллельны. Значит, при построении нескольких прямых в одной системе координат прямые будут параллельны, если коэффициент b у них разный, а k – одинаковый. Пусть b = 0, тогда линейная функция примет вид y = kx – это прямая пропорциональность, график которой пройдет через начало координат (0;0) не зависимо от значения k. Итак, коэффициент b отвечает за перемещение графика линейной функции вдоль оси Оу [7]. Если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции у = kx + b. 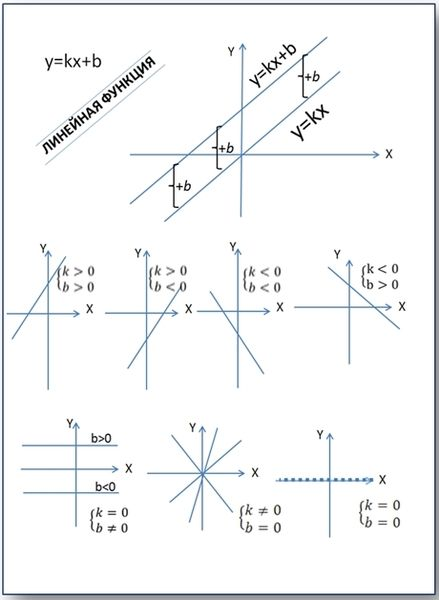 |
