интегрирование. Интегрирование простейших рациональных дробей. Интегрирование простейших рациональных дробей. Интегрирование правильной дробнорациональной функции
 Скачать 240.5 Kb.
|
|
Интегрирование простейших рациональных дробей. 1. Интегрирование правильной дробно-рациональной функции Сразу пример и типовой алгоритм решения интеграла от дробно-рациональной функции. Пример 1 Найти неопределенный интеграл.  Шаг 1. Первое, что мы ВСЕГДА делаем при решении интеграла от дробно-рациональной функции – это выясняем следующий вопрос: является ли дробь правильной? Данный шаг выполняется устно: Сначала смотрим на числитель и выясняем старшую степень многочлена: 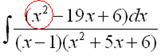 Старшая степень числителя равна двум. Теперь смотрим на знаменатель и выясняем старшую степень знаменателя. Напрашивающийся путь – это раскрыть скобки и привести подобные слагаемые, но можно поступить проще, в каждой скобке находим старшую степень 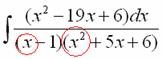 и мысленно умножаем:  – таким образом, старшая степень знаменателя равна трём. Совершенно очевидно, что если реально раскрыть скобки, то мы не получим степени, больше трёх.Вывод: Старшая степень числителя СТРОГО меньше старшей степени знаменателя, значит, дробь является правильной. Если бы в данном примере в числителе находился многочлен 3, 4, 5 и т.д. степени, то дробь была бы неправильной. Шаг 2. Разложим знаменатель на множители. Смотрим на наш знаменатель:  Вообще говоря, здесь уже произведение множителей, но, тем не менее, задаемся вопросом: нельзя ли что-нибудь разложить еще. Решаем квадратное уравнение:  Дискриминант больше нуля, значит, трехчлен действительно раскладывается на множители: 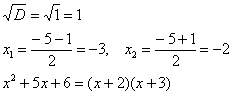 Общее правило: ВСЁ, что в знаменателе МОЖНО разложить на множители – раскладываем на множители Начинаем оформлять решение:  Шаг 3. Методом неопределенных коэффициентов раскладываем подынтегральную функцию в сумму простых (элементарных) дробей. Смотрим на нашу подынтегральную функцию:  Неплохо бы нашу большую дробь превратить в несколько маленьких. Например, вот так:  Такое разложение существует и единственно. Только коэффициенты  мы пока не знаем, отсюда и название – метод неопределенных коэффициентов.Находим эти коэффициенты: В левой части приводим выражение к общему знаменателю:  Теперь благополучно избавляемся от знаменателей (т.к. они одинаковы):  В левой части раскрываем скобки, неизвестные коэффициенты при этом пока не трогаем: Коэффициенты лучше внести в скобки: Составляем систему линейных уравнений. Сначала разыскиваем старшие степени: 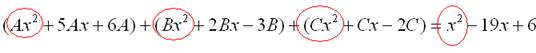 И записываем соответствующие коэффициенты в первое уравнение системы: 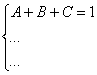 Далее процесс идет по снижающейся траектории, отмечаем все «иксы»:  Записываем соответствующие коэффициенты во второе уравнение системы: 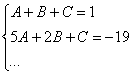 И, наконец, подбираем свободные члены.  Система готова: 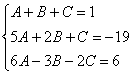 Решаем систему: 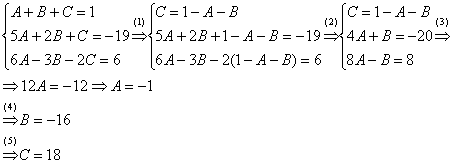 (1) Из первого уравнения выражаем  и подставляем его во 2-е и 3-е уравнения системы. На самом деле можно было выразить (или другую букву) из другого уравнения, но в данном случае выгодно выразить именно из 1-го уравнения, поскольку там самые маленькие коэффициенты.(2) Приводим подобные слагаемые во 2-м и 3-м уравнениях. (3) Почленно складываем 2-е и 3-е уравнение, при этом, получая равенство  , из которого следует, что  (4) Подставляем во второе (или третье) уравнение, откуда находим, что  (5) Подставляем и в первое уравнение, получая  .После решения системы всегда полезно сделать проверку – подставить найденные значения в каждое уравнение системы, в результате всё должно «сойтись».Почти приехали. Коэффициенты найдены, при этом: Чистовое оформление задание должно выглядеть примерно так:  Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: 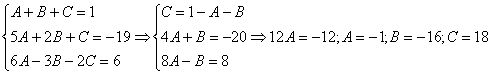  Как видите, основная трудность задания состояла в том, чтобы составить и решить систему линейных уравнений. А на завершающем этапе всё не так сложно: используем свойства линейности неопределенного интеграла и интегрируем. Обращаю внимание, что под каждым из трёх интегралов у нас сложная функция, которую проинтегрировали Методом замены переменной в неопределенном интеграле. Проверка: Дифференцируем ответ: 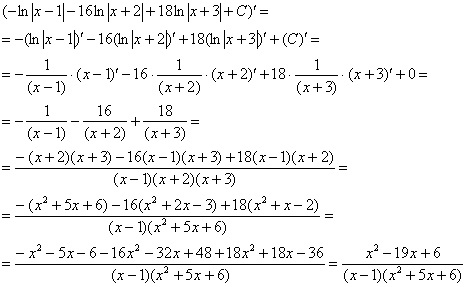 Получена исходная подынтегральная функция, значит, интеграл найден правильно. В ходе проверки пришлось приводить выражение к общему знаменателю, и это не случайно. Метод неопределенных коэффициентов и приведение выражения к общему знаменателю – это взаимно обратные действия. Пример 2 Найти неопределенный интеграл.  Решение:  Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: 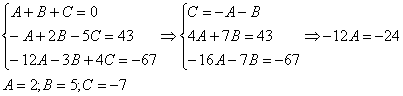    Комментарий: в правой части у нас нет слагаемого с  , поэтому в первом уравнении системы ставим справа ноль. Пример 3 Представить функцию  в виде суммы элементарных дробей с неизвестными коэффициентами.Шаг 1. Проверяем, правильная ли у нас дробь Старшая степень числителя: 2 Старшая степень знаменателя: 8  , значит, дробь является правильной.Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Очевидно, что нет, всё уже разложено. Квадратный трехчлен  не раскладывается в произведение по указанным выше причинам. Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей. В данном случае, разложение имеет следующий вид:  Смотрим на наш знаменатель:  При разложении дробно-рациональной функции в сумму элементарных дробей можно выделить три принципиальных момента: 1) Если в знаменателе находится «одинокий» множитель в первой степени (в нашем случае  ), то вверху ставим неопределенный коэффициент (в нашем случае  ). Примеры №1,2 состояли только из таких «одиноких» множителей.2) Если в знаменателе есть кратный множитель  , то раскладывать нужно так: – то есть последовательно перебрать все степени «икса» от первой до энной степени. В нашем примере два кратных множителя:  и  , еще раз взгляните на приведенное мной разложение и убедитесь, что они разложены именно по этому правилу.3) Если в знаменателе находится неразложимый многочлен второй степени (в нашем случае ), то при разложении в числителе нужно записать линейную функцию с неопределенными коэффициентами (в нашем случае  с неопределенными коэффициентами  и  ).Пример 5 Найти неопределенный интеграл.  Шаг 1. Очевидно, что дробь является правильной:  Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Можно. Здесь сумма кубов  . Раскладываем знаменатель на множители, используя формулу сокращенного умножения   Шаг 3. Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:  Обратите внимание, что многочлен  неразложим на множители (проверьте, что дискриминант отрицательный), поэтому вверху мы ставим линейную функцию  с неизвестными коэффициентами, а не просто одну буковку.Приводим дробь к общему знаменателю:   Составим и решим систему: 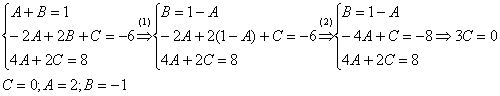 (1) Из первого уравнения выражаем  и подставляем во второе уравнение системы (это наиболее рациональный способ).(2) Приводим подобные слагаемые во втором уравнении. (3) Почленно складываем второе и третье уравнения системы. Все дальнейшие расчеты, в принципе, устные, так как система несложная. 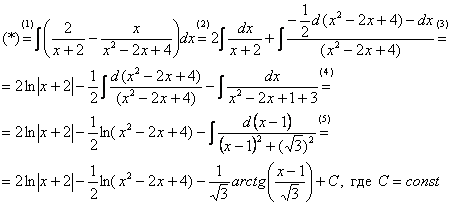 (1) Записываем сумму дробей в соответствии с найденными коэффициентами .(2) Используем свойства линейности неопределенного интеграла. Что произошло во втором интеграле? С этим методом Вы можете ознакомиться в последнем параграфе урока Интегрирование некоторых дробей. (3) Еще раз используем свойства линейности. В третьем интеграле начинаем выделять полный квадрат (предпоследний параграф урока Интегрирование некоторых дробей). (4) Берём второй интеграл, в третьем – выделяем полный квадрат. (5) Берём третий интеграл. Готово. А вот вам еще пара примеров для самостоятельного решения, один похожий, другой – труднее. Пример 6 Найти неопределенный интеграл.  Решение:  Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: 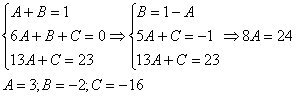    2. Интегрирование неправильной дробно-рациональной функцииПерейдем к рассмотрению случая, когда старшая степень числителя больше либо равна старшей степени знаменателя. Пример 8 Найти неопределенный интеграл.  Совершенно очевидно, что данная дробь является неправильной:  Основной метод решения интеграла с неправильной дробно-рациональной функций – это деление числителя на знаменатель. Сначала рисуем «заготовку» для деления: 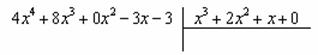 ВСЕ недостающие степени (и (или) свободные члены) без пропусков записываем в ОБОИХ многочленах с нулевыми коэффициентами Теперь маленькая задачка, на какой множитель нужно умножить 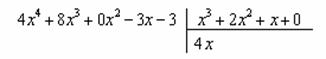, чтобы получить  ? Очевидно, что на  : Далее умножаем 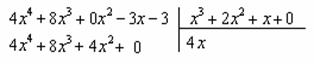сначала на , потом – на  , потом – на  , потом – на 0 и записываем результаты слева: Проводим черточку и производим вычитание (из верха вычитаем низ): 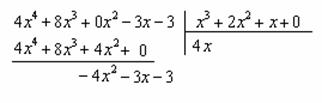 Старшая степень остатка  равна двум, старшая степень делителя  – больше, она равна трём, значит, больше разделить не удастся. Если бы изначально у нас был в числителе многочлен пятой степени, то алгоритм деления увеличился бы на один шаг.Итак, наше решение принимает следующий вид:  Делим числитель на знаменатель: 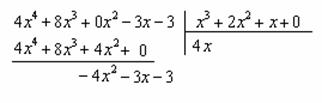 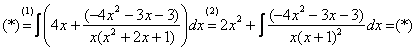(1) Что дало деление? Много хорошего: теперь у нас два слагаемых, первое – интегрируется совсем просто, а второе – правильная дробь, которую мы решать уже умеем. После деления всегда желательно выполнять проверку. В рассматриваемом примере можно привести к общему знаменателю  , и в результате получится в точности исходная неправильная дробь  (2) От первого слагаемого сразу берем интеграл. Знаменатель дроби раскладываем на множители Дальше всё идет по накатанной схеме: Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: 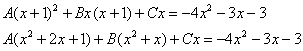 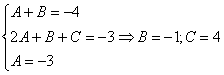   Готово. Пример 9 Найти неопределенный интеграл.  Решение: 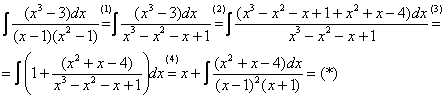 (1) Здесь неправильная дробь, поскольку старшие степени числителя и знаменателя равны: 3 = 3. Для того чтобы разделить числитель на знаменатель придётся временно раскрыть скобки в знаменателе. (2)-(3) Теперь можно разделить  на знаменатель  , но делать этого… я не буду. Можно поступить хитрее. Используем прием, который рассмотрен в первом параграфе урока Интегрирование некоторых дробей.(4) От первого слагаемого сразу берем интеграл. Знаменатель оставшейся, уже правильной, дроби снова записываем в виде произведения множителей. Тут я немного подсократил разложение, надеюсь, всем понятно, что  Далее накатанная колея… Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: 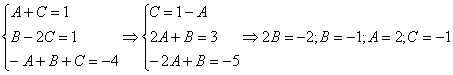    |