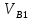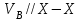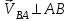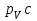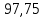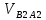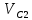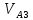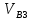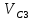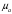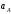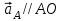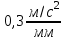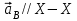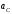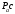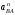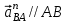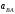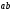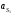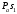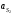Решение 1 Построение кинематической схемы механизма
 Скачать 152.36 Kb. Скачать 152.36 Kb.
|
|
Плешков Никита Максимович, НТКбп-20-1 Кинематический расчёт кривошипно-ползунного механизма (рис.3.2). Определение скоростей точек звеньев и угловых скоростей звеньев для заданного положения механизма Дано: Угловая скорость кривошипа 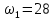 рад/сек. рад/сек.Размеры звеньев: ОА = 25мм, АВ = 80мм, АС = 30мм, Точки S1, S2, S3 находятся на серединах полных длин соответствубщих звеньев Решение 3.1.1. Построение кинематической схемы механизма Построим кинематическую схему механизма в заданном положении в масштабе М1:1, то есть  м/мм (рис.3.2). м/мм (рис.3.2).3.1.2. Определение скорости точки А кривошипа  м/с м/сЗадаём отрезок, изображающий вектор скорости 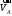 на плане: на плане:  мм. мм.Найдем масштаб плана скоростей:  . .Вектор скорости 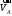 направлен перпендикулярно кривошипу ОА в сторону угловой скорости направлен перпендикулярно кривошипу ОА в сторону угловой скорости 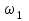 . . Покажем это направление на кинематической схеме механизма (рис.3.2). 3.1.3. Определение скорости точки В Запишем векторное уравнение: 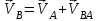 , (3.3) , (3.3)где 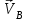 - вектор скорости точки В шатуна и ползуна; - вектор скорости точки В шатуна и ползуна;  - вектор относительной скорости точки В относительно точки А. - вектор относительной скорости точки В относительно точки А. Уравнение (3.3) решается графически с помощью построения плана скоростей. План скоростей имеет вид треугольника, сторонами которого являются скорости 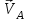 , , 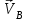 , ,  . .3.1.4. Построение плана скоростей (рис.3.2) Из полюса плана скоростей 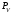 откладываем отрезок откладываем отрезок  мм перпендикулярно кривошипу ОА в направлении угловой скорости мм перпендикулярно кривошипу ОА в направлении угловой скорости  . .Из конца вектора 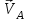 (точка a) проводим вектор (точка a) проводим вектор  . Он направлен перпендикулярно шатуну АВ. Из полюса (точка pV) проводим вектор . Он направлен перпендикулярно шатуну АВ. Из полюса (точка pV) проводим вектор 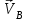 . Он направлен параллельно оси Х-Х. На пересечении двух проведённых направлений получим точку b. . Он направлен параллельно оси Х-Х. На пересечении двух проведённых направлений получим точку b. Вычисляем скорости. Для этого измеряем длины полученных отрезков 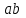 и и 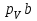 , подставляем в формулы в миллиметрах и умножаем их на масштаб , подставляем в формулы в миллиметрах и умножаем их на масштаб 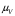 . .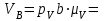 36 36 0,01=0,36 м/с; 0,01=0,36 м/с;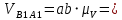 74 74  0,01=0,74 м/с. 0,01=0,74 м/с.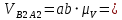 67 67  0,01=0,67 м/с. 0,01=0,67 м/с.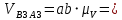 70 70  0,01=0,7 м/с. 0,01=0,7 м/с.3.1.5. Определение скорости точки С Воспользуемся следствием из теоремы подобия: скорость любой третьей точки жесткого звена определится путем построения фигуры или линии подобной данному звену. Составим пропорцию: 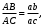 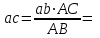 27,75 мм. 27,75 мм.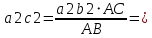 25,125 мм. 25,125 мм.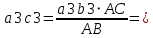 26,26 мм. 26,26 мм.Данный отрезок откладываем на продолжении отрезка ab. Точку c соединяем с полюсом pV. Величина скорости точки С: 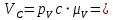 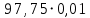 =0,9775 м/с. =0,9775 м/с.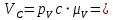 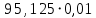 =0,95125 м/с. =0,95125 м/с.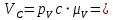  =0,9625 м/с. =0,9625 м/с.3.1.6. Определение угловой скорости шатуна АВ  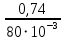 =9,25 рад/сек =9,25 рад/сек 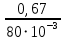 =8,375 рад/сек =8,375 рад/сек 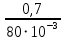 =8,75 рад/сек =8,75 рад/секДля определения направления 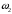 переносим вектор переносим вектор  в точку В шатуна АВ и смотрим, как она движется относительно точки А. Направление этого движения соответствует в точку В шатуна АВ и смотрим, как она движется относительно точки А. Направление этого движения соответствует  . В данном случае угловая скорость . В данном случае угловая скорость 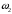 направлена против часовой стрелки (см. рис.3.2). Все полученные результаты занесем в таблицу 3.2. направлена против часовой стрелки (см. рис.3.2). Все полученные результаты занесем в таблицу 3.2.Таблица 3.2 Определение скоростей
Кинематический расчёт кривошипно-ползунного механизма (рис.3.3). Определение ускорений точек звеньев и угловых ускорений звеньев для заданного положения механизма 3.2.1. Определение ускорения точки А Полагая, что угловая скорость  является постоянной, угловое ускорение кривошипа является постоянной, угловое ускорение кривошипа 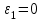 . Поэтому полное ускорение . Поэтому полное ускорение 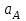 равно нормальному ускорению равно нормальному ускорению  : : 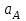 = = . .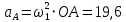 м/с2. м/с2.Задаём отрезок, изображающий вектор ускорения 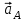 на плане: на плане:  мм. мм. Масштаб плана ускорений 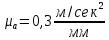 . .3.2.2. Определение ускорения точки В Запишем векторное уравнение:  . . где  - вектор относительного ускорения. - вектор относительного ускорения.Раскладываем  на нормальную и касательную составляющие: на нормальную и касательную составляющие: 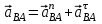 . .Следовательно, 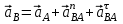 . (3.4) . (3.4)Нормальное относительное ускорение точки В относительно точки А равно: 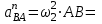 6,8 6,8 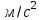 . .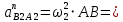 5,6 5,6 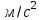 . .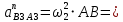 6,1 6,1 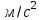 . .Найдём отрезок, изображающий вектор ускорения 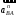 на плане: на плане: 22,7 мм. 22,7 мм. 18,7 мм. 18,7 мм. 20,3 мм. 20,3 мм.3.2.3. Построение плана ускорений План ускорений представляет из себя фигуру любой произвольной формы, сторонами которой являются векторы ускорений 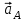 , ,  , , 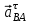 , , 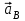 . .Для построения плана ускорений необходимо знать направления векторов скоростей. Вектор ускорения точки А 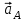 направлен параллельно кривошипу ОА от точки А к точке О. Из полюса плана ускорений pa откладываем отрезок направлен параллельно кривошипу ОА от точки А к точке О. Из полюса плана ускорений pa откладываем отрезок  мм, соответствующий этому ускорению. мм, соответствующий этому ускорению. Вектор нормального ускорения точки В относительно точки А  направлен параллельно шатуну АВ от точки В к точке А. Из точки a плана ускорений откладываем отрезок направлен параллельно шатуну АВ от точки В к точке А. Из точки a плана ускорений откладываем отрезок  мм, соответствующий этому ускорению. мм, соответствующий этому ускорению. Вектор касательного ускорения точки В относительно точки А 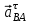 направлен перпендикулярно шатуну АВ. Из точки n плана ускорений проводим направление вектора ускорения направлен перпендикулярно шатуну АВ. Из точки n плана ускорений проводим направление вектора ускорения 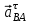 . . Вектор ускорения точки В ползуна 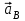 направлен параллельно оси Х-Х. Из полюса pa проводим направление вектора ускорения направлен параллельно оси Х-Х. Из полюса pa проводим направление вектора ускорения 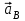 . . Две прямые линии, проведённые из точек n и paв указанных направлениях, пересекаются в точке b. Соединяем точки а и b. Вычисляем ускорения. Для этого измеряем длины полученных отрезков  , ,  , , 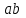 , подставляем в формулы в миллиметрах и умножаем их на масштаб , подставляем в формулы в миллиметрах и умножаем их на масштаб  . .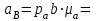 м/с2; м/с2; м/с2; м/с2; 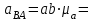 м/с2. м/с2.Полученные результаты занесем в таблицу 3.3. 3.2.4. Определение ускорения точки С Воспользуемся следствием из теоремы подобия. Составим пропорцию: 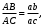 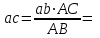 мм. мм. Данный отрезок откладываем на продолжении отрезка ab. Точку c соединяем с полюсом pa . Величина ускорения точки С: 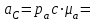  м/с2. м/с2.3.2.5. Определение ускорения точкиS1 – центра масс кривошипа 1 Воспользуемся следствием из теоремы подобия. Составим пропорцию:  , , 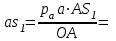 мм. мм.Данный отрезок откладываем на прямой paa от точки a. Величина ускорения: 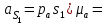 м/с2. м/с2.3.2.6. Определение ускорения точкиS2– центра масс шатуна 2 Воспользуемся следствием из теоремы подобия. Составим пропорцию: 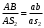 , , 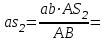 м/с2. м/с2.Данный отрезок откладываем на прямой ab от точки a. Точку s2 соединяем с полюсом pa. Величина ускорения: 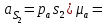 м/с2. м/с2.3.2.7.Определение углового ускорения шатуна АВ Величина ускорения: 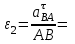 рад/сек2 рад/сек2 . . Для определения направления  переносим вектор переносим вектор 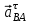 в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует  . В данном случае угловое ускорение . В данном случае угловое ускорение 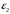 направлено против часовой стрелки (см. рис.3.3). направлено против часовой стрелки (см. рис.3.3).Таблица 3.3 Значения ускорений
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


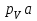

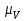 =
=