нн. Практическая работа теория вероятностей. Решение 1 Пусть событие а из карточек получили слово река. Событие состоит в одновременном наступлении событий вытянули букву Р
 Скачать 18.83 Kb. Скачать 18.83 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Теория вероятностей и математическая статистика Группа ММ20М671 Студент И.О. Фамилия Евсеева О.С. МОСКВА 2021 1. Буквы, составляющие слово РАКЕТА, написаны по одной на шести карточках; карточки перемешаны и положены в пакет. 1.1. Чему равна вероятность того, что, вынимая четыре буквы, ПОЛУЧИМ слово РЕКА? 1.2. Какова вероятность сложить слово КАРЕТА при вынимании всех букв? Решение: 1.1 Пусть событие А – из карточек получили слово РЕКА. Событие состоит в одновременном наступлении событий «вытянули букву Р», «вытянули букву Е», «вытянули букву К», «вытянули букву А». Так как эти события зависимы (число карточек уменьшается после того, как была вытянута буква), то воспользуемся теоремой умножения вероятностей зависимых событий: 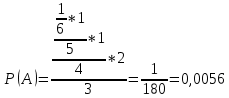 1.2 Пусть событие B – из карточек сложили слово КАРЕТА. Событие состоит в одновременном наступлении событий «вытянули букву К», «вытянули букву А», «вытянули букву Р», «вытянули букву Е», «вытянули букву Т», «вытянули букву А». Так как эти события зависимы (число карточек уменьшается после того, как была вытянута буква), то воспользуемся теоремой умножения вероятностей зависимых событий: 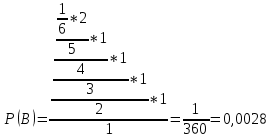 Ответ: вероятность получить слово РЕКА составляет 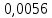 ; вероятность сложить слово КАРЕТА составляет ; вероятность сложить слово КАРЕТА составляет 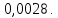 2. Дискретная случайная величина 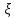 задана следующим законом распределения: задана следующим законом распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение. Решение: 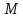 ( (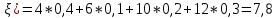 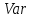 ( (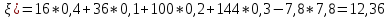 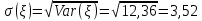 Ответ: 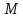 ( (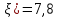 ; ; 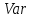 ( (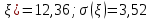 3. Возможные значения дискретной случайной величины равны: -2, 1, 4. При условии, что заданы математическое ожидание 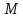 ( (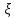 ) = 1.9, а также ) = 1.9, а также 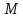 ( (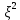 )) = 7.3, найти вероятности )) = 7.3, найти вероятности 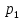 , , 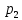 , , 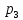 , которые соответствуют дискретным значениям случайной величины. , которые соответствуют дискретным значениям случайной величины.Решение: 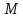 ( (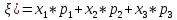 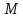 ( (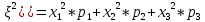 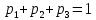 Подставим наши значения в систему: 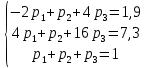 Найдем решение системы методом Гаусса: 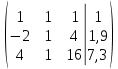 Сложим первую строку, умножив ее на 2, со второй строкой; сложим первую строку, умножив ее на -4, с третьей строкой: 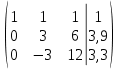 Сложим вторую строку с третьей: 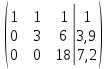 Получим: 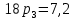 => => 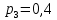 3 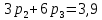 => => 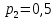 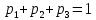 => => 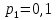 Ответ: 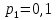 ; ; 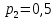 ; ; 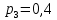 |