электротехника. Для электрической схемы. Решение 1 Зададим направление движению тока, и движения тока в контуре
 Скачать 259.74 Kb. Скачать 259.74 Kb.
|
|
Для электрической схемы, выбранной в соответствии с № варианта: 1. составить систему уравнений для определения токов в ветвях методом законов Кирхгофа; Эквивалентно преобразовать схему до двух контуров; Рассчитать токи во всех ветвях схемы: методом контурных токов, методом узловых потенциалов. Составить баланс мощностей. 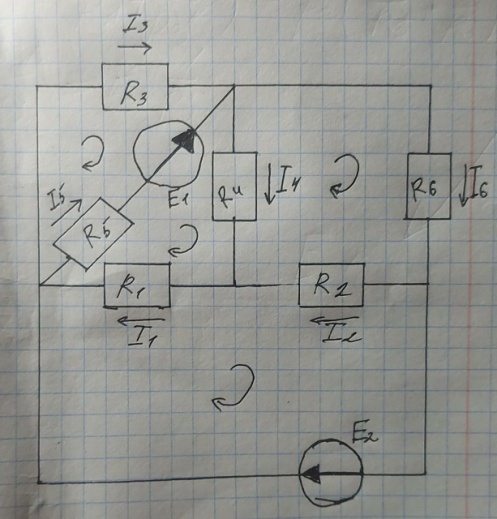 Дано: Е1=20 В Е2=40 В R1=2 Ом R2=1 Ом R3=30 Ом R4=10 Ом R5=10 Ом R6=20 Ом Решение: 1)Зададим направление движению тока, и движения тока в контуре. 2)Всего в схеме 7 ветвей Рв=7,ветвей с источником тока нет Рт=0,число неизвестных токов равно Р=(Рв-Рв)=7-0=7, количество узлов – q=4, количество уравнений по первому закону Кирхгофа равно (q-1)=4-1=3 , число уравнений по второму закону Кирхгофа n=P-(q-1)=7-(4-1)=4. Составим уравнение по первому закону Кирхгофа: 1)для узла а - 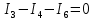 2)для узла b - 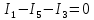 3)для узла c - 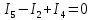 По второму закону Кирхгофа Для контуров: 1) 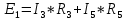 2) 2)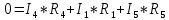 3) 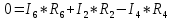 4) 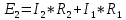 Составим систему уравнения 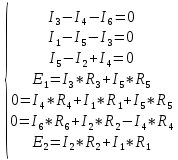 Подставим числовые значения 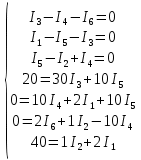 2)Эквивалентно преобразовать схему до двух контуров Складываем два последовательных сопротивления 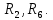 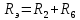 П 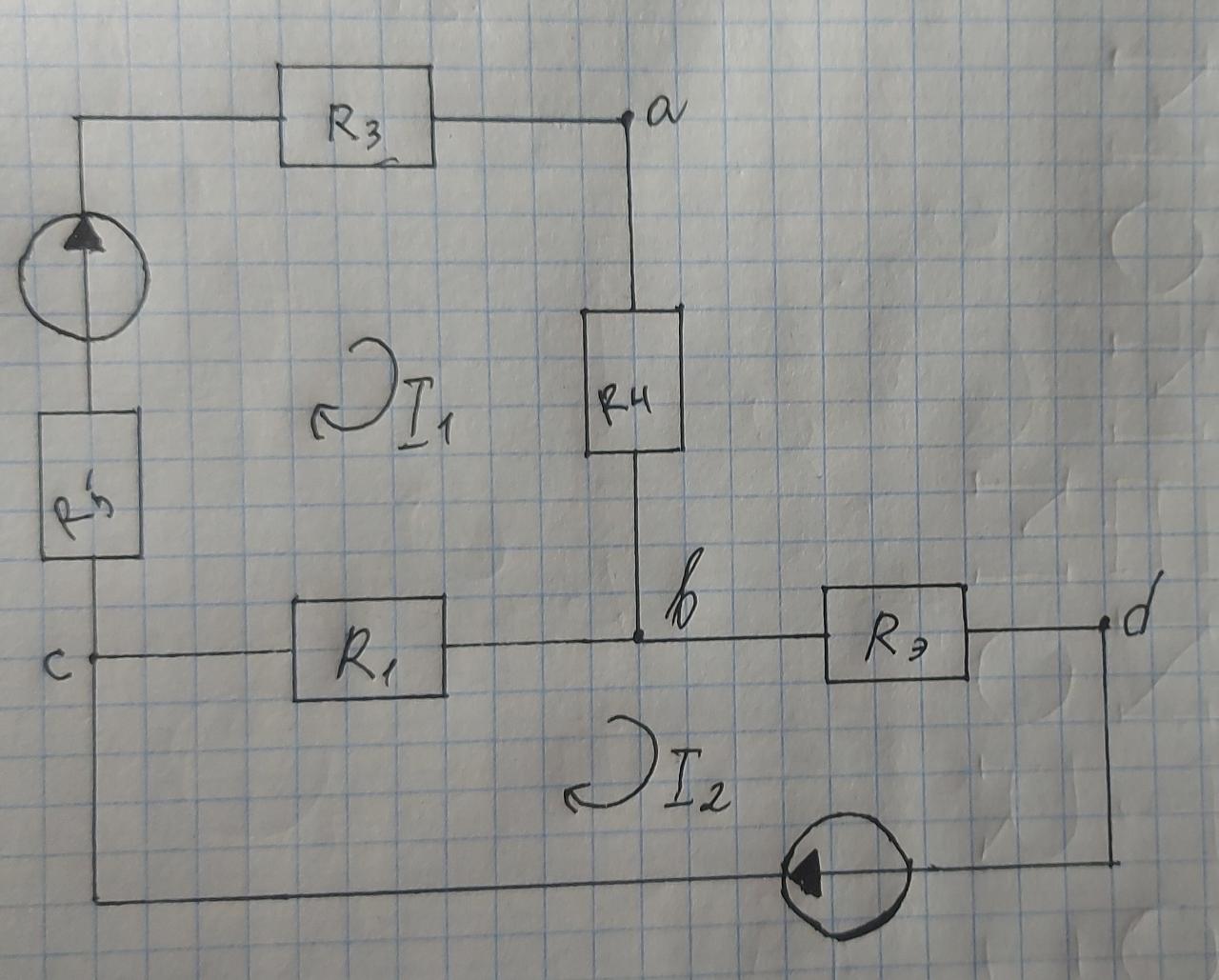 олучаем схему 3.Рассчитать токи во всех ветвях схемы А)Методом контурных токов Метод основывается на том свойстве, что ток в любой ветви цепи может быть представлен в виде алгебраической суммы независимых контурных токов, протекающих по этой ветви. Выберем направления контурных токов, которые обозначим I11 и I22. Составим систему уравнений для контуров 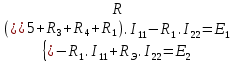 Подставим числовые значения 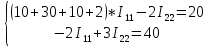 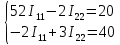 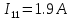 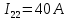 Б)Методом узловых потенциалов Составить систему уравнений методом узловых потенциалов для узлов a,b и c. 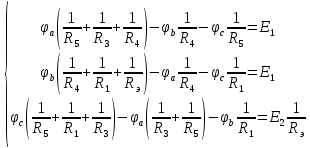 4.Составить баланс мощности 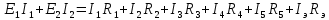 1.Начертить комплексную расчетную схему. 2.Рассчитать комплексные сопротивления элементов цепи для частоты тока и напряжения 50 Гц. 3.Выбрать любой метод расчета и определить в комплексной форме токи и напряжения во всех ветвях. 4.Проверить результаты расчета, рассчитав баланс мощности цепи. 5.Определить показание ваттметра. 6.Построить векторную диаграмму токов и напряжений, соответствующую рассчитанной схеме. 1 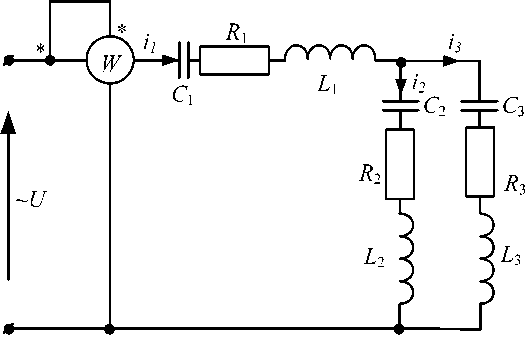 ) ) 2) Комплексное сопротивление индуктивного элемента: 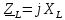 , , 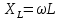 , ,Пример задачи 2.1. В схеме (рис.2.5) рассчитать комплексные сопротивления элементов (круговая частота 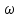 =314 рад/с): =314 рад/с): 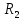 = 20 Ом, = 20 Ом, 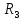 = 40 Ом, = 40 Ом, 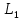 = 64мГн, = 64мГн, 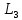 = 128 мГн, = 128 мГн, 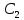 = 159 мкФ. Определить полное комплексное сопротивление цепи = 159 мкФ. Определить полное комплексное сопротивление цепи 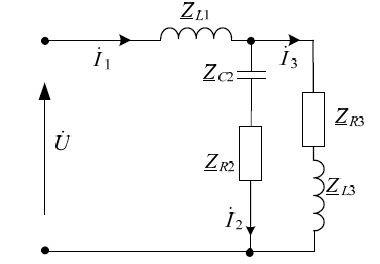 Рис. 2.5 Решение: В схеме определим комплексные сопротивления элементов: 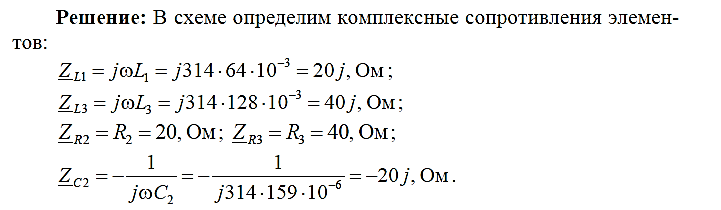 Упростим схему, за счет сложения последовательно соединенных сопротивлений (рис. 2.6) 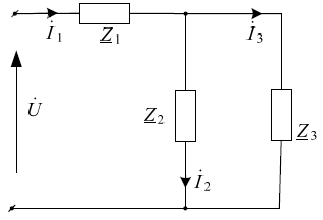 Рис. 2.6 Z1 = ZL1 = 20j= 20 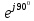 , Ом , ОмZ2 = ZR2 + ZC2 = 20 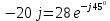 , Ом , ОмZ3 = ZR3 + ZL3 = 40 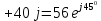 , Ом , ОмТеперь можно сложить параллельно соединенные сопротивления 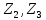 : :Z23 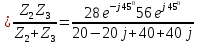 = = 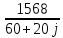 = = 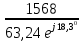 = 24,8 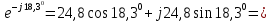 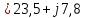 , Ом; , Ом;Сопротивления 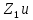 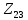 соединены последовательно: соединены последовательно:Z = Z1 + Z23 = 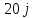 + +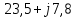 =23,5 + =23,5 + 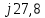 = 36 = 36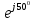 . . |
