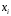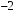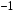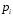Задачи по теории вероятностей. Теория вероятностей Козлова. Решение 443 11 всего карандашей в коробке способами можно извлечь 7 карандашей из коробки
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
m=2; n=1 В коробке находится 4 синих, 4 красных и 3 зеленых карандаша. Одновременно вынимают 7 карандашей. Найти вероятность того, что среди них будет 3 синих и 2 красных карандаша. Решение: 4+4+3 = 11 – всего карандашей в коробке 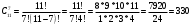 способами можно извлечь 7 карандашей из коробки способами можно извлечь 7 карандашей из коробки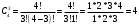 способами можно извлечь 3 синих карандаша способами можно извлечь 3 синих карандаша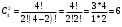 способами можно извлечь 2 красных карандаша способами можно извлечь 2 красных карандаша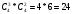 способами можно извлечь набор карандашей способами можно извлечь набор карандашейПо классическому определению вероятности Р(А) = 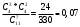 – вероятность того, что среди 7 извлеченных карандашей будет 3 синих и 2 красных карандаша. – вероятность того, что среди 7 извлеченных карандашей будет 3 синих и 2 красных карандаша.На склад поступили 2 ящика, в которых содержится по 20 годных деталей и 4 бракованных и 1 ящик, в котором содержится 20 годных деталей и 3 бракованных. Наудачу выбирается ящик и из него наудачу извлекается деталь. Найти вероятность того, что вынутая деталь является годной. Решение: Событие А – вынута годная деталь Н1 – выбран ящик, в котором 20 годных и 4 бракованных детали Н2 – выбран ящик, в котором 20 годных и 3 бракованных детали Вероятности гипотез равны: Р(Н1) = 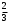 ; Р(Н2) = ; Р(Н2) = 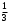 Условные вероятности события А при этих гипотезах равны: Р(А/Н1) = 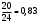 ; Р(А/Н2) = ; Р(А/Н2) = 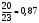 По формуле общей вероятности Р(А) = 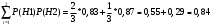 1.3 Вероятность попадания стрелка в мишень при одном выстреле равна 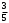 . Производится 5 выстрелов. Найти вероятность того, что он промахнется не более двух раз. . Производится 5 выстрелов. Найти вероятность того, что он промахнется не более двух раз.Решение: Поскольку по условиям задачи р = 0,6, то q = 1-p = 1-0,6 = 0,4 По условиям n = 5, m = 3 по формуле Бернулли получим: 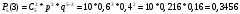 1.4 Ряд распределения дискретной случайной величины Х имеет вид:
Найти вероятности 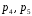 , если математическое ожидание M[X] = 0,6. Построить многоугольник распределения. Найти функцию распределения , если математическое ожидание M[X] = 0,6. Построить многоугольник распределения. Найти функцию распределения 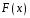 и построить ее график. Вычислить дисперсию и построить ее график. Вычислить дисперсию 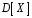 и среднее квадратическое отклонение. и среднее квадратическое отклонение. Решение: Сумма вероятностей ряда распределения 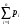 = 1, в нашем случае = 1, в нашем случае 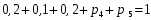 Математическое ожидание находится по формуле 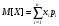 , в нашем случае M[X] = -2*0,2 -1*0,1+0*0,2+2р4+3р5=0,6 , в нашем случае M[X] = -2*0,2 -1*0,1+0*0,2+2р4+3р5=0,6Получаем систему двух уравнений: 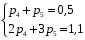 , решая которую получаем , решая которую получаем 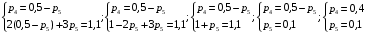 Таким образом, Таким образом, 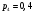 ; ; 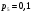 Тогда ряд распределения дискретной случайной величины Х имеет вид:
Построим многоугольник распределения, для этого в прямоугольной системе координат строим точки 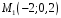 , , 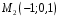 , , 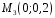 , , 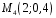 , , 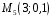 , затем соединяем эти точки отрезками прямых. Ломаная , затем соединяем эти точки отрезками прямых. Ломаная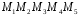 является многоугольником распределения данной случайной величины. является многоугольником распределения данной случайной величины.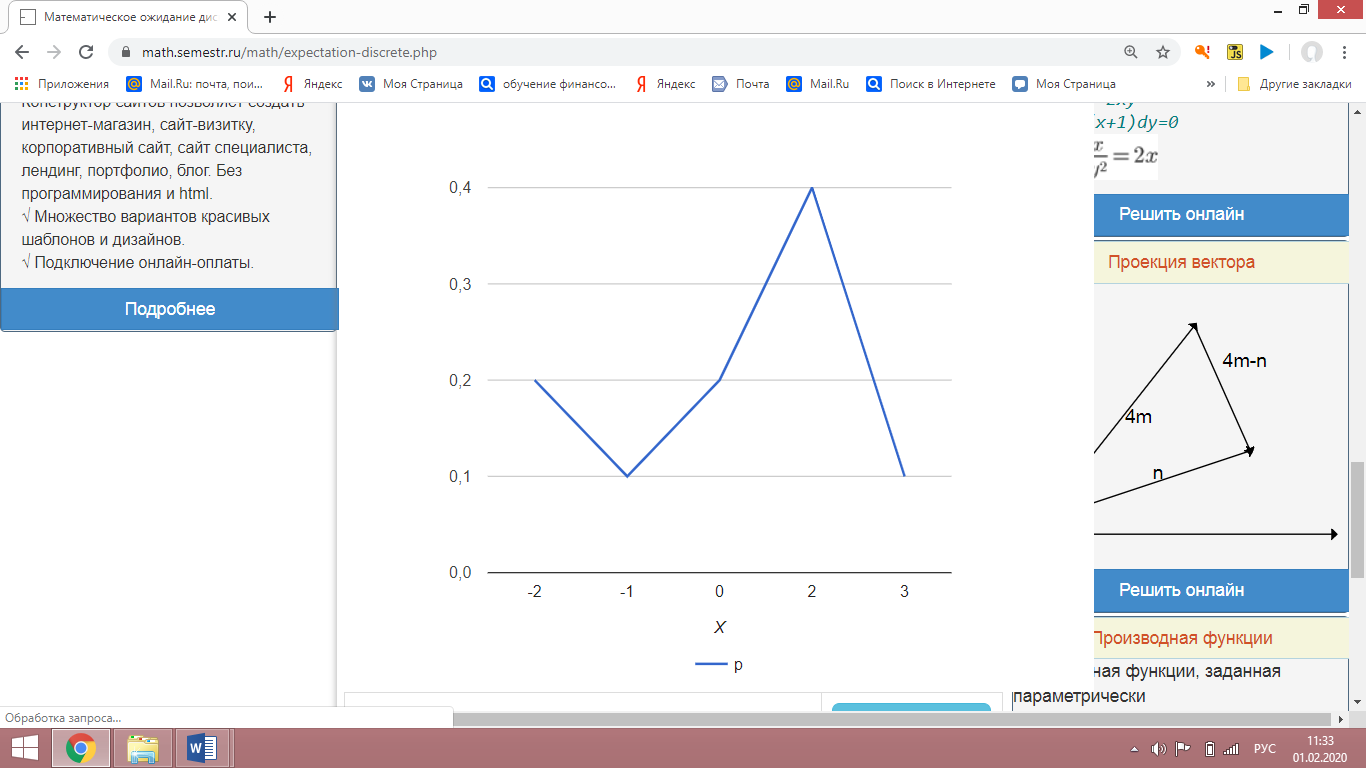 Функция распределения F(X) F(x≤-2) = 0 F(-2< x ≤-1) = 0,2 F(-1< x ≤0) = 0,1 + 0,2 = 0,3 F(0< x ≤2) = 0,2 + 0,3 = 0,5 F(2< x ≤3) = 0,4 + 0,5 = 0,9 F(x>3) = 1 График представленной функции распределения будет выглядеть следующим образом: 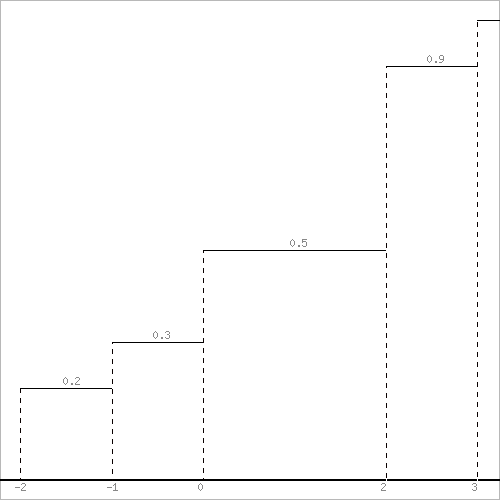 Дисперсия D[X] D[X] = 22*0,2 + 12*0,1 + 02*0,2 + 22*0,4 + 32*0,1 - 0.62 = 3.04 Среднее квадратическое отклонение σ(x). 1.5 Плотность распределения непрерывной случайной величины Х имеет вид: 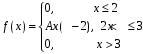 . .Найти: а) параметр A; б) функцию распределения 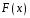 ; ;в) вероятность попадания случайной величины Х в интервал 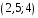 ; ;г) математическое ожидание 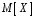 и дисперсию и дисперсию 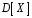 . .Решение: а) Найдем параметр A из условия: 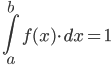 Для нашей функции: 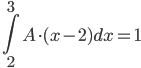 или A/2-1 = 0 Откуда, A = 2 б) Функция распределения 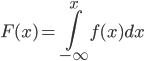 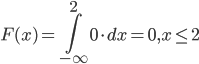 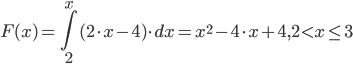 F(x) = 1, x > 3 в) Вероятность того, что случайная величина Х примет значение из интервала [a,b] равна: P(a < x < b) = F(b) – F(a) P(2,5 < x < 4) = F(4) – F(2,5) = (42 – 4·4+4) – (2,52 – 4·2.5+4) = 1 – 0,25 = 0,75 г) Математическое ожидание 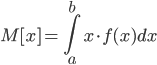 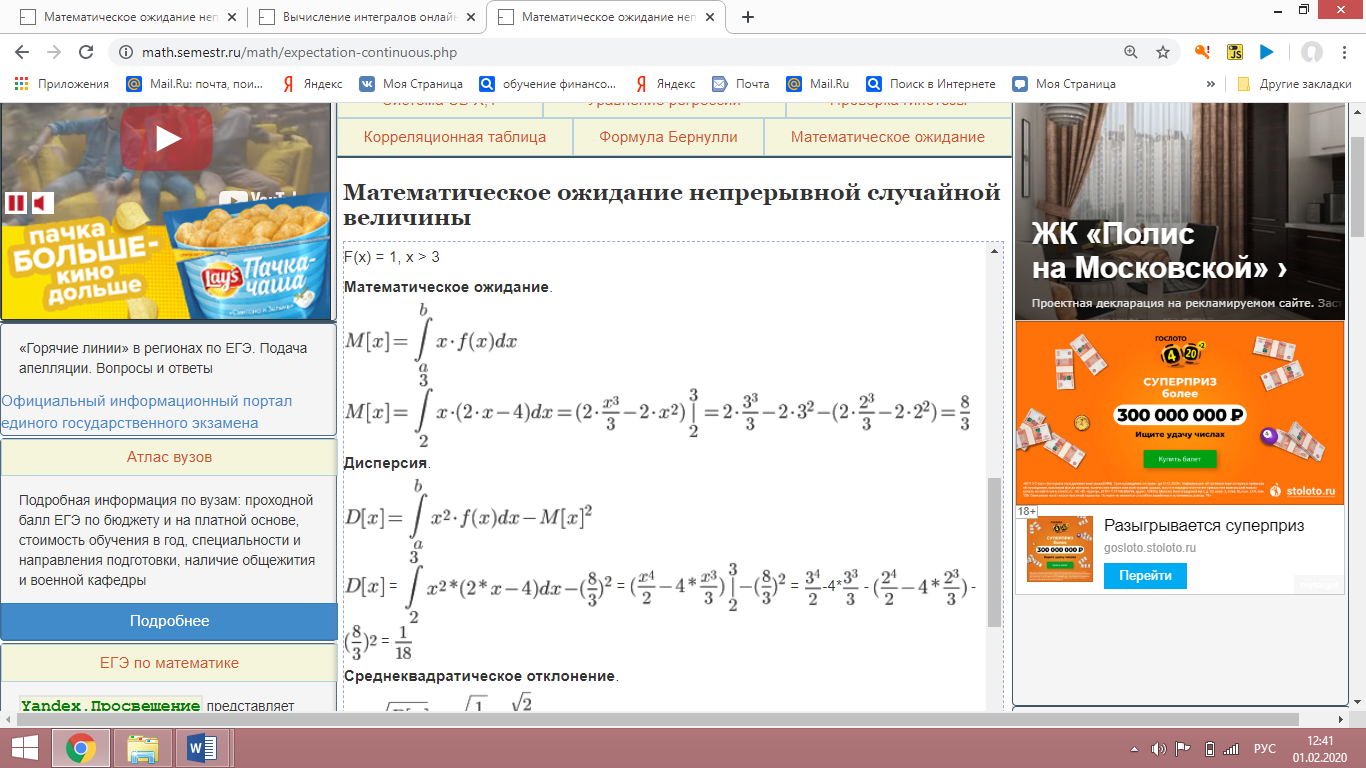 Дисперсия. 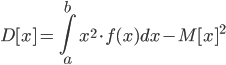  |