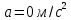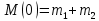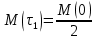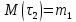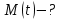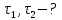ргз по механике. ргз механика. Решение 9,81 Рис. Эскиз траектории движения камня
 Скачать 379.6 Kb. Скачать 379.6 Kb.
|
|
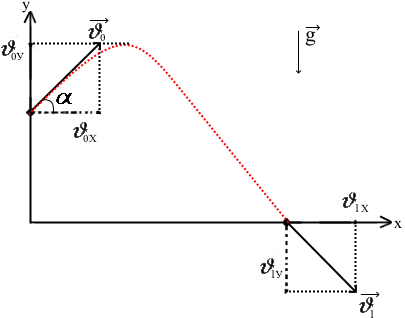
Задача 1.3 Постановка задачи: Камень бросили с крутого берега вверх под углом 45 градусов к горизонту со скоростью 15 м/с. С какой скоростью он упал в воду, если время полета 4 с. Сопротивлением воздуха пренебречь. Построить график наклона вектора скорости к горизонту и график траектории движения камня.
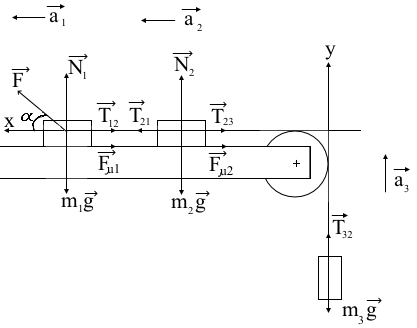
Математическая модель Закон, по которому изменяется вектор скорости в зависимости от времени: 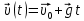 В проекциях: 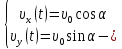 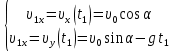 Модуль вектора скорости: 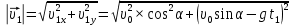 Вычислим:  Графическая часть Зависимость у(t): 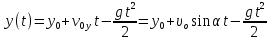 В момент попадания в воду 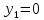 : :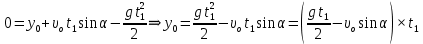 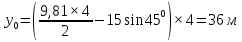 Запишем уравнение траектории движения: 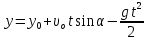 = =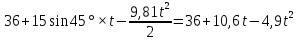 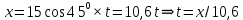 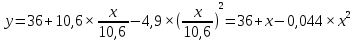 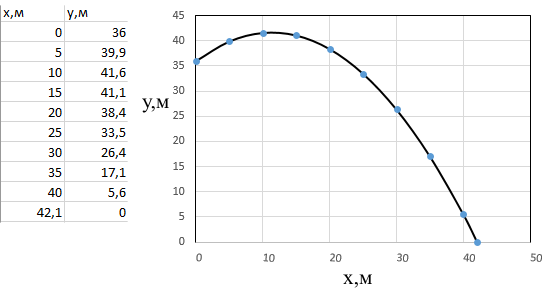 Рис. 1.2. График траектории движения камня Выявим зависимость угла между вектором скорости и осью Ox от времени: 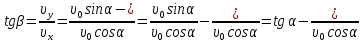 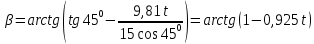 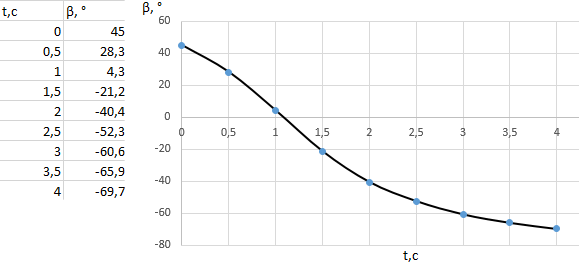 Рис. 1.3 График наклона вектора скорости к горизонту Анализ решения По графикам можно заметить соответствие увеличения координаты y до определённой точки, и затем её снижение, положительным значениям угла между вектором скорости и горизонтом, а затем их убывание ниже 0. Данное соответствие свидетельствует о смене направления вертикального движения на противоположное, что соответствует броску тела под углом к горизонту. Ответ: 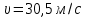 Задача 2.4 Постановка задачи: Определить ускорения тел и силу натяжения нити (рис.2.1). Массы тел равны 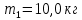 , , 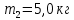 , , 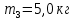 , коэффициент трения , коэффициент трения  , угол , угол 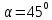 , , 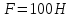 . Постройте график зависимости силы натяжения нити. . Постройте график зависимости силы натяжения нити.
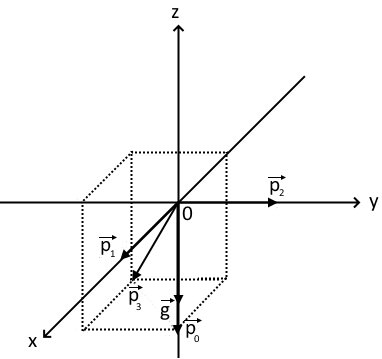
Математическая модель Составим систему уравнений согласно 2 закону Ньютона в векторной форме: 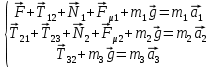 Согласно 3 закону Ньютона, считая нить и блок идеальными, имеем: 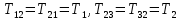 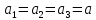 Перепишем систему в проекциях на оси координат для каждого из трёх тел: 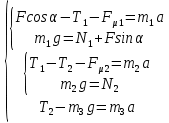 Выразим силы трения: 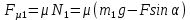 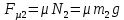 Получим систему уравнений: 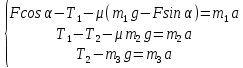 Выразим из неё  + 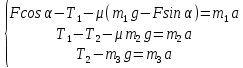 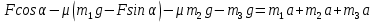 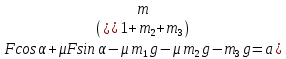 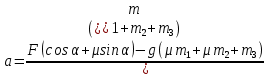 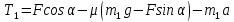 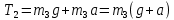 Вычислим выраженные величины: 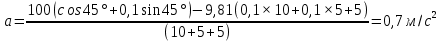 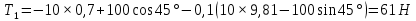 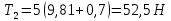 Графическая часть Для построения графика зависимости силы натяжения нити от угла 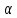 , сначала выясним зависимость , сначала выясним зависимость 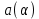 . .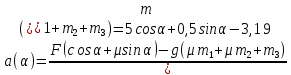 Найдём зависимости сил натяжения нити от угла α: 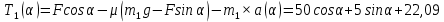 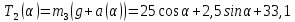 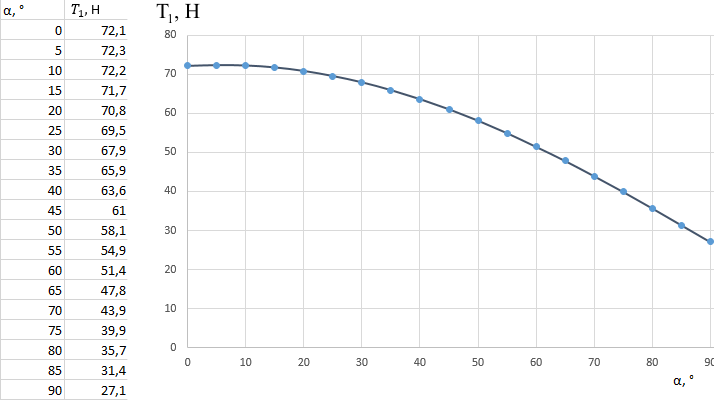 Рис. 2.2 График зависимости T1(α) 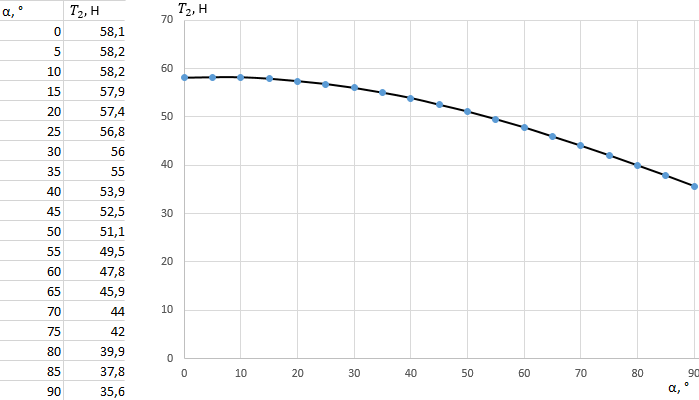 Рис. 2.3 График зависимости T2(α) Анализ решения На приведённых графиках можно заметить, что при увеличении градусной меры угла α сила натяжения нити уменьшается. Этому соответствует уменьшение величины проекции силы F на ось Ox и, соответственно, уменьшение величины ускорения 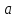 . Также график подтверждает, что для заданного угла вычисления были проведены верно. . Также график подтверждает, что для заданного угла вычисления были проведены верно.Ответ: 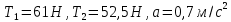 Задача 3.7 Постановка задачи: В момент, когда скорость падающей вниз гранаты составила 4 м/с, граната разорвалась на три одинаковых осколка. Два осколка разлетелись в горизонтальной плоскости под прямым углом друг к другу со скоростью 5 м/с каждый. Найти скорость третьего осколка сразу после разрыва. Построить графики траектории движения осколков гранаты.
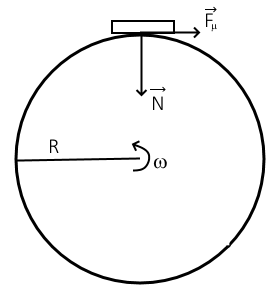
Математическая модель Так как 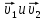 перпендикулярно направлены, то удобно выбрать такую систему координат, чтобы перпендикулярно направлены, то удобно выбрать такую систему координат, чтобы 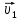 был направлен по оси Ox, был направлен по оси Ox, 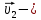 по оси Oy, по оси Oy, 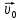 по отрицательному направлению оси Oz. по отрицательному направлению оси Oz.Согласно закону сохранения импульса, имеем: 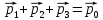 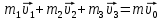 Так как по условию 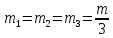 , то , то 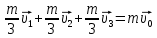 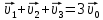 Перепишем уравнение в проекциях: 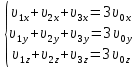 Выразим проекции вектора 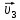 : :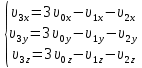 Вычислим: 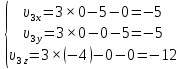 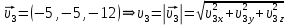 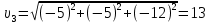 м/с м/сГрафическая часть Для построения графиков траектории движения осколков нужно выяснить уравнения движения для каждого из них. Первый осколок: 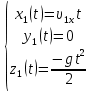 => => 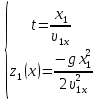 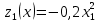 Второй осколок: 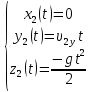 => => 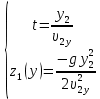 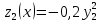 Третий осколок: Так как осколок движется по всем трём координатам, рассмотрим его движение в плоскости, образованной проекцией 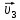 на плоскость xOy и осью Oz. на плоскость xOy и осью Oz.Введём в этой плоскости ось Ou, в которой лежит проекция 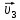 на плоскость xOy, причем направление от начала координат до конца проекции возьмём положительным для оси Ou. Тогда на плоскость xOy, причем направление от начала координат до конца проекции возьмём положительным для оси Ou. Тогда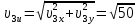 =7,07 =7,07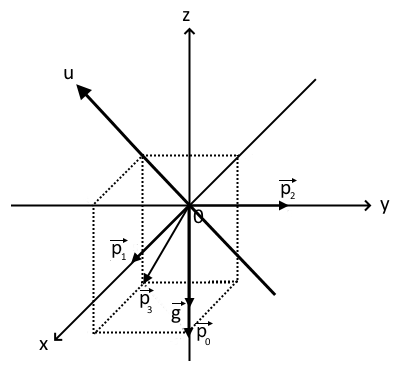 Рис. 3.2 Положение новой оси Ou в системе координат Для плоскости uOz имеем: 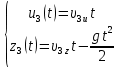 => =>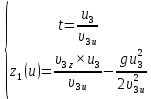 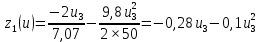 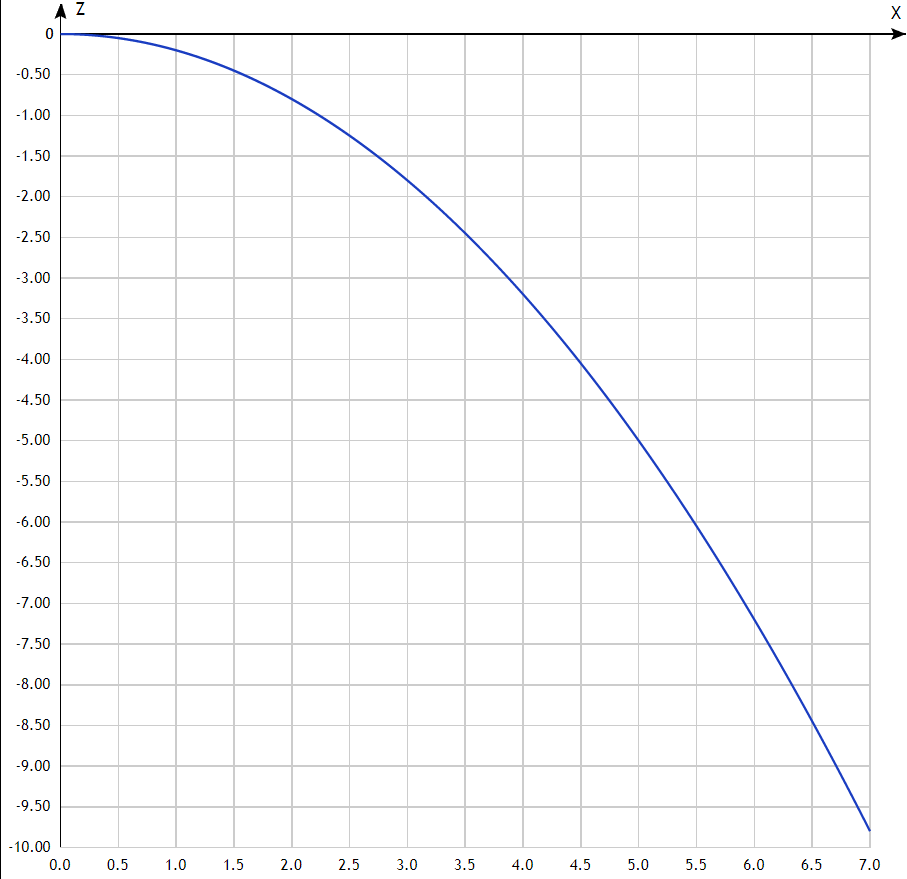 Рис. 3.3 График траектории движения первого осколка 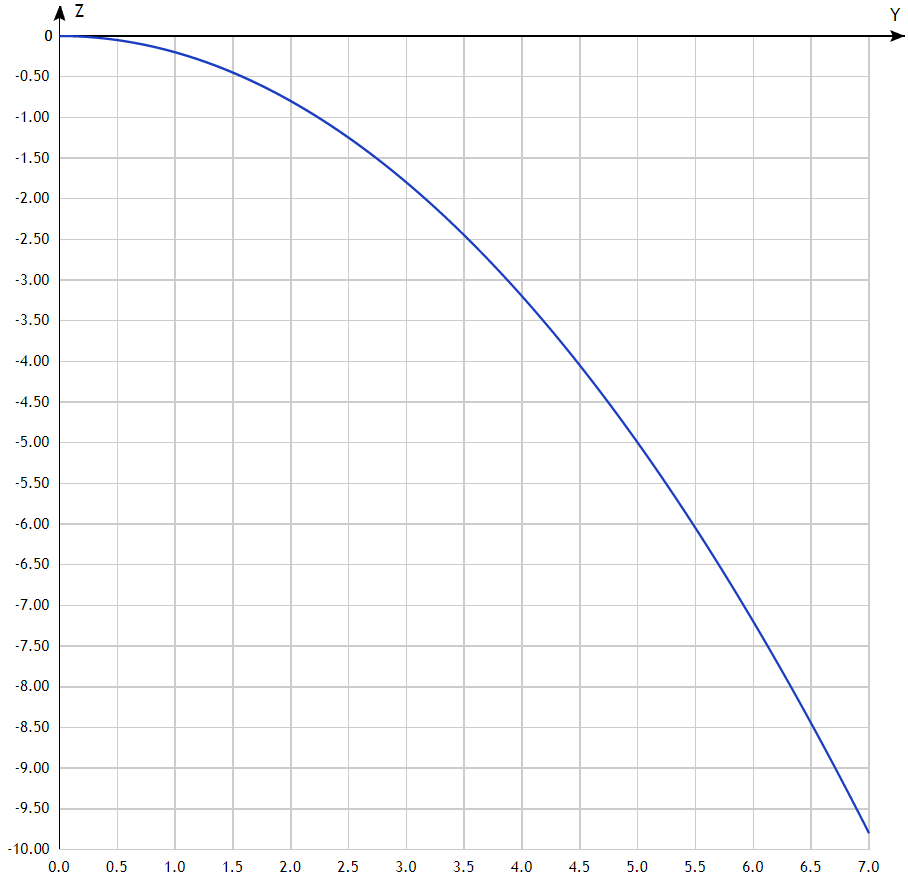 Рис. 3.4 График траектории движения второго осколка 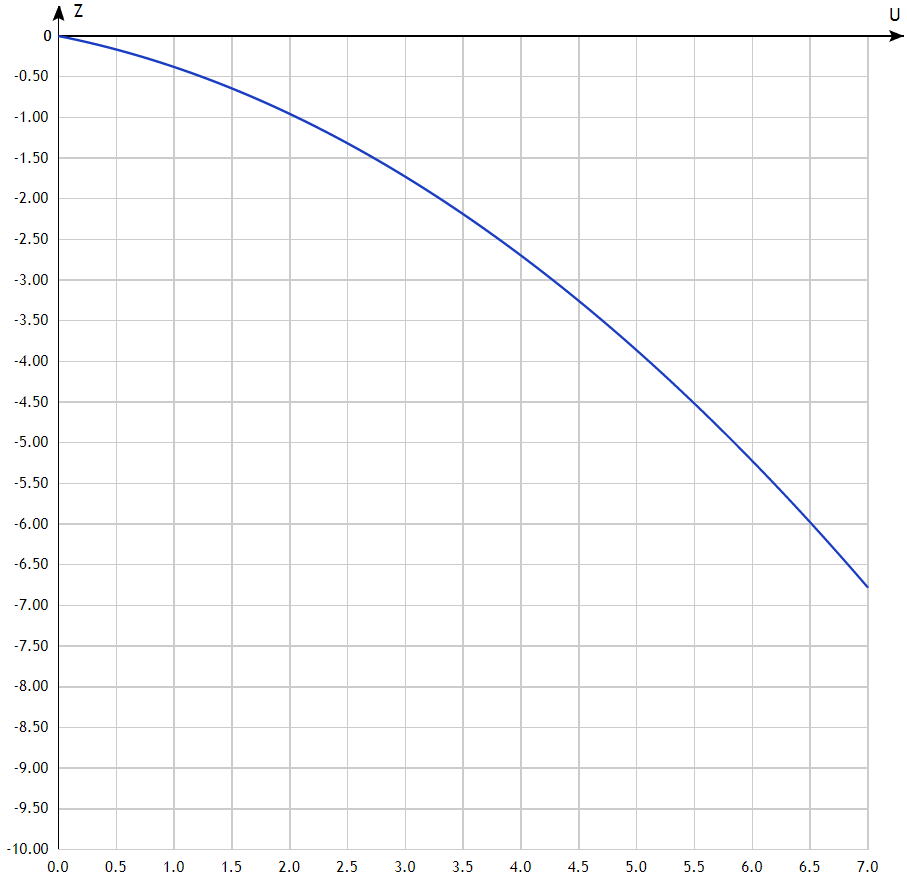 Рис. 3.5 График траектории движения третьего осколка Анализ решения Графики траекторий движения первого и второго осколков представлены одинаковыми функциями, но с разными аргументом, так как скорости направлены по разным осям координат, в соответствии с условием задач. Так же можно по графикам заметить, что траектория движения третьего осколка медленнее убывает, что связано с большей величиной проекции 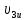 . Импульс третьего осколка в горизонтальной плоскости компенсирует импульс первого и второго осколков, а в вертикальной плоскости сонаправлен с импульсом всей гранаты, что соответствует закону сохранения импульса. . Импульс третьего осколка в горизонтальной плоскости компенсирует импульс первого и второго осколков, а в вертикальной плоскости сонаправлен с импульсом всей гранаты, что соответствует закону сохранения импульса.Ответ: 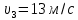 Задача 4.8 Постановка задачи: Сплошной однородный маховик массой 20 кг и радиусом 100 мм вращается, совершая 20 об/с. С какой силой нужно прижать к нему тормозную колодку, чтобы он остановился за 5 с, если коэффициент трения равен 0.2? Определить работу торможения и построить график угловой скорости и кинетической энергии маховика.
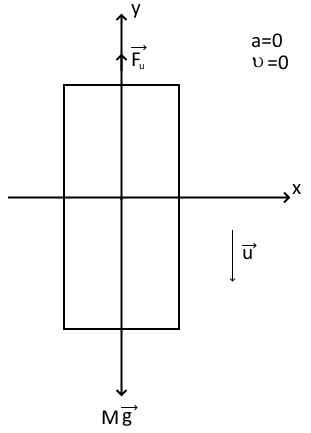
Математическая модель Момент силы постоянен по условию задачи. Исходя из закона изменения момента импульса: 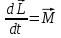 В проекции на ось вращения: 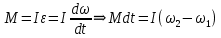 Силой торможения в задаче является сила трения 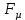 , а плечом является радиус диска, соответственно , а плечом является радиус диска, соответственно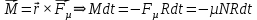 Так как диск в итоге останавливается, то 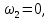 в то время как в то время как 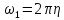 Момент инерции однородного диска: 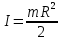 Получаем уравнение: 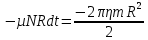 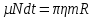 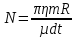 Работа силы равна изменению кинетической энергии диска: 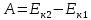 Кинетическая энергия тела, вращающегося вокруг неподвижной оси: 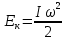 Получаем уравнение: 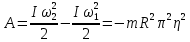 Вычислим: 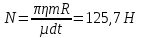 A = 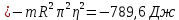 Графическая часть 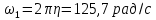 Найдем зависимость 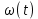 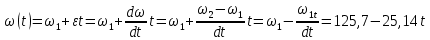 Найдем зависимость 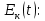 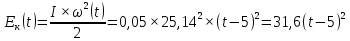  Рис. 4.2 График зависимости 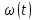 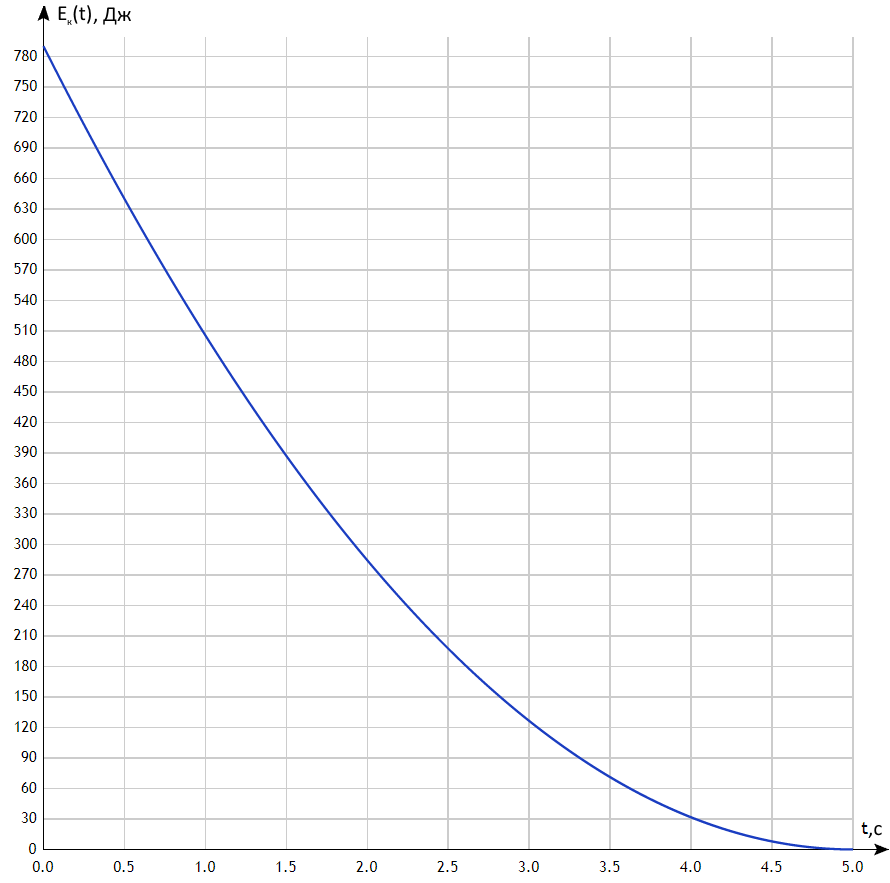 Рис. 4.2 График зависимости 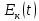 Анализ решения График зависимости угловой скорости от времени представлен убывающей прямой, что свидетельствует о постоянном угловом ускорении, которое вызвано тормозящей диск силой трения. За 5 секунд угловая скорость достигает нуля, что соответствует остановке вращения по условию задачи. Также на графике изменения кинетической энергии прослеживается замедление вращения диска до его полной остановки по прошествии 5 секунд. Изменение кинетической энергии за этот промежуток времени соответствует выполненной работе A. Ответ:  Задача 5.9 Постановка задачи: По какому закону должна меняться во времени масса ракеты (вместе с топливом), чтобы она во время работы оставалась неподвижной в поле тяжести Земли, если скорость  газовой струи относительно ракеты постоянна? Определите время, через которое полная масса ракеты уменьшится вдвое, также время, по истечении которого ракета израсходует весь запас топлива. Принять: масса ракеты без топлива газовой струи относительно ракеты постоянна? Определите время, через которое полная масса ракеты уменьшится вдвое, также время, по истечении которого ракета израсходует весь запас топлива. Принять: масса ракеты без топлива 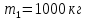 , масса топлива , масса топлива 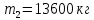 , скорость газовой струи , скорость газовой струи 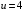 км/с. Построить графики временной зависимости массы ракеты. км/с. Построить графики временной зависимости массы ракеты.
Математическая модель Уравнение Мещерского для системы в векторной форме: 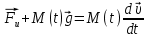 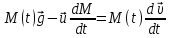 В проекции: 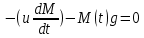 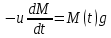 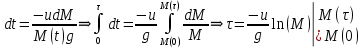 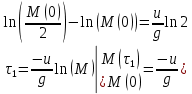 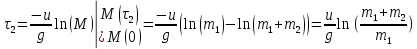 Вычислим: 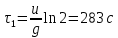 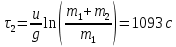 Найдем закон изменения массы во времени: 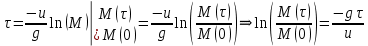 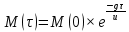 Графическая часть 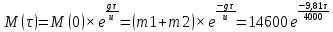 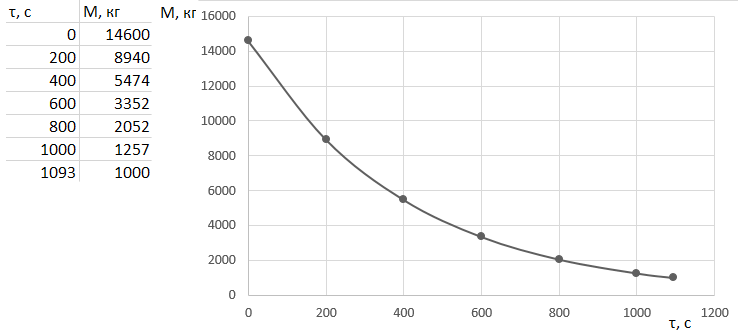 Рис. 5.2 График изменения полной массы ракеты с течением времени Анализ решения По графику можно заметить явное уменьшение массы ракеты, связанное с уменьшением остатка топлива в ней. Достижение полной массы ракеты в 1000 кг эквивалентное массе ракеты без топлива соответствует полной растрате топлива за найденное время 1093 с. Ответ: 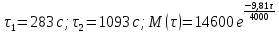 |

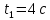
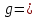 9,81
9,81 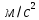
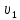 - ?
- ? 
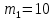 кг
кг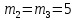 кг
кг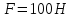

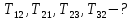
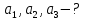
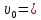 4 м/с
4 м/с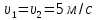
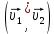 = 90°
= 90°
 = 9,81 м/с2
= 9,81 м/с2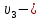 ?
?
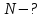
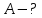
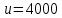 м/с
м/с