Решение a 2 a 1 f 3 f 2 f 1 v iv iii ii i 0,35 0,35 0,1 0,6 0,1
 Скачать 476.56 Kb. Скачать 476.56 Kb.
|
d= 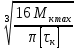 = = 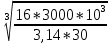 = 79,9 мм. = 79,9 мм.Принимаем d = 80 мм. Из условия жесткости d = 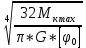 = = 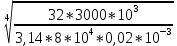 = 66,1 мм. = 66,1 мм. Принимаем d = 68 мм. Требуемый диаметр получился больше из расчета на прочность, поэтому его принимаем как окончательный d = 80 мм. Ответ: d = 80 мм. Задача 96 Для стальной балки, жестко защемленной одним концом и нагруженной, как показано на схеме, построить эпюры поперечных сил и изгибающих моментов. Принять из условия прочности необходимый размер двутавра, считая [σ] = 160 МПа. Дано: 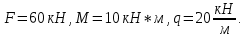 Решение Определим реакции в заделке: Сумма моментов всех сил относительно точки A должна равняться нулю: ∑MA = - MA – q*l/2 + F*l + M = - MA - 20·62/2 + 60·6 + 10 = - MA + 10 = 0, MA = 10 кН*м; Сумма проекций всех сил на вертикальную ось должна равняться нулю: ∑Y = RA – q*l + F = RA - 20·6 + 60 = RA - 60 = 0, RA = 60 кН; Для проверки вычислим сумму моментов всех сил относительно точки B: ∑MB = - MA - RA*l + q*l2/2 + M = -10 - 60·6 + 20·62/2 + 10 = -10 - 360 + 360 + 10 = 0; Реакции определены правильно. Определим значения поперечных сил Q и изгибающих моментов M на участках балки.  RA RA      MA q = 20 кН/м M = 10 кН*м MA q = 20 кН/м M = 10 кН*м             A I II B   5 м 1 м F = 60 кН 5 м 1 м F = 60 кН   l l 60 60  Эпюра Q, Эпюра Q,  кН кН  100 60 -60 100 60 -60   50 Эпюра M, 50 Эпюра M, 10 кН*м 10 кН*мРис. 1. Схема нагружения и эпюры Q и M Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках. Участок I (0 ≤ z ≤ 5): Поперечная сила Q: QI(z) = RA – q*z = 60 – 20*z = - 20z + 60; Значения Q на краях отрезка: QI(0) = - 20·0 + 60 = 60 кН; QI(5) = - 20·5 + 60 = - 40 кН; На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения: QI(z) = - 20z + 60 = 0, z1 = 60/20 = 3 м; Изгибающий момент M: MI(z) = MA + RA z – q*z2/2 = 10 + 60z - 20z2/2 = - 10z2 + 60z + 10; Значения M на краях отрезка: MI(0) = - 10·02 + 60·0 + 10 = 10 кН*м; MI(5) = - 10·52 + 60·5 + 10 = 60 кН*м; Локальный экстремум в точке z1 = 3 м: MI(3) = - 10·32 + 60·3 + 10 = 100 кН*м; Участок II (5 ≤ z ≤ 6): Поперечная сила Q: QII(z) = RA – q*z = - 20z + 60; Значения Q на краях отрезка: QII(5) = - 20·5 + 60 = - 40 кН; QII(6) = - 20·6 + 60 = - 60 кН; Изгибающий момент M: MII(z) = MA + RA z – q*z2/2 - M1 = 10 + 60z - 20z2/2 - 10 = 10 + 60z - 20z2/2 - 10 = - 10z2 + 60z; Значения M на краях отрезка: MII(5) = - 10·52 + 60·5 = 50 кН*м; MII(6) = - 10·62 + 60·6 = 0. По результатам расчетов строим эпюры Qи M (рис. 1). Из условия прочности подберем размер двутавра.  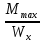 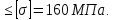 Wx 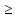 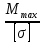 = = 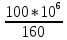 = 625*103 мм3 = 625 см3. = 625*103 мм3 = 625 см3.Из сортамента проката принимаем двутавр №33 (Wx = 597 см3). Определим степень перегрузки балки 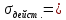 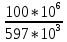 = 167,5 МПа. = 167,5 МПа.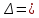 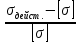 *100% = *100% = 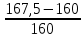 *100% = 4,7% < 5%, что допустимо. *100% = 4,7% < 5%, что допустимо.Ответ: Двутавр №33. Задача 104 Для заданной двухопорной балки определить реакции опор, построить эпюры поперечных сил и изгибающих моментов. Подобрать из условия прочности размеры поперечного сечения прямоугольника или круга, приняв для прямоугольника h = 2b. Считать [σ] = 150 МПа. Дано: 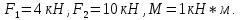 Решение Определим реакции опор. Сумма моментов всех сил относительно точки B должна равняться нулю: ∑MB = RA*10 - F1*4 - F2*8 - M = RA·10 - 4·4 - 10·8 - 1 = RA·10 - 97 = 0, RA = 97/10 = 9,7 кН; Сумма моментов всех сил относительно точки A должна равняться нулю: ∑MA = RB*10 - F1*14 + F2*2 - M = RB·10 - 4·14 + 10·2 - 1 = RB·10 - 37 = 0, RB = 37/10 = 3,7 кН; Для проверки вычислим сумму проекций всех сил на вертикальную ось: ∑Y = - RA + RB - F1 + F2 = - 9,7 + 3,7 - 4 + 10 = 0; Реакции определены правильно. Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках. Участок I (0 ≤ z ≤ 2): Поперечная сила Q: QI(z) = RA = - 9,7; Значения Q на краях отрезка: QI(0) = - 9,7 кН; QI(2) = - 9,7 кН; Изгибающий момент M: MI(z) = RA z = - 9,7z; Значения M на краях отрезка: MI(0) = - 9,7·0 = 0; MI(2) = - 9,7·2 = - 19,4 кН*м;    F2 = 10 кН М = 1 кН*м RBF1 = 4 кН F2 = 10 кН М = 1 кН*м RBF1 = 4 кН           А В А В  IIIIIIIV IIIIIIIV    RA 2м 4м 4м 4м RA 2м 4м 4м 4м 4 4 4 4  0,3 0,3 Эпюра Q, 0,3 0,3 Эпюра Q,   кН кН        - 9,7 - 9,7 Эпюра М, кН*м -17,2 -16 - 19,4 -18,2 Рис. 1. Схема нагружения и эпюры Qи M Участок II (2 ≤ z ≤ 6): Поперечная сила Q: QII(z) = - RA + F2 = - 9,7 + 10 = 0,3; Значения Q на краях отрезка: QII(2) = 0,3 кН; QII(6) = 0,3 кН; Изгибающий момент M: MII(z) = - RA z - F2(z - 2) = - 9,7z + 10(z - 2) = 0,3z - 20; Значения M на краях отрезка: MII(2) = 0,3·2 - 20 = - 19,4 кН*м; MII(6) = 0,3·6 - 20 = - 182 кН*м; Участок III (6 ≤ z ≤ 10): Поперечная сила Q: QIII(z) = - RA + F2 = - 9,7 + 10 = 0,3; Значения Q на краях отрезка: QIII(6) = 0,3 кН; QIII(10) = 0,3 кН; Изгибающий момент M: MIII(z) = - RA z + F2(z - 2) + M = - 9,7z + 10(z - 2) + 1 = 0,3z - 19; Значения M на краях отрезка: MIII(6) = 0,3·6 - 19 = - 17,2 кН*м; MIII(10) = 0,3·10 - 19 = - 16 кН*м; Участок IV (10 ≤ z ≤ 14): Поперечная сила Q: QIV(z) = - RA + RB + F2 = - 9,7 + 3,7 + 10 = 4; Значения Q на краях отрезка: QIV(10) = 4 кН; QIV(14) = 4 кН; Изгибающий момент M: MIV(z) = - RA z + RB(z - 10) + F2(z - 2) + M1 = - 9,7z + 3,7(z - 10) + 10(z - 2) + 1 = = 4z - 56; Значения M на краях отрезка: MIV(10) = 4·10 - 56 = - 16 кН*м; MIV(14) = 4·14 - 56 = 0. По результатам расчетов построены эпюры Q и M(рис. 1). Подберем из условия прочности размеры поперечного сечения прямоугольника или круга, приняв для прямоугольника h = 2b. Запишем условие прочности 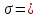 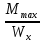 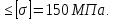 Тогда Wx 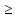 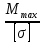 = = 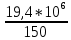 = 129333 мм3. = 129333 мм3.Моменты сопротивлений сечений: 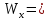 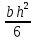 = = 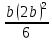 = = 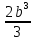 – момент сопротивления прямоугольника; – момент сопротивления прямоугольника;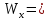 |
