Решение a 2 a 1 f 3 f 2 f 1 v iv iii ii i 0,35 0,35 0,1 0,6 0,1
 Скачать 476.56 Kb. Скачать 476.56 Kb.
|
|
Вариант 43 Задача 66 Двухступенчатый стальной брус нагружен силами F1 ,F2, F3. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение Δl свободного конца бруса, приняв Е = 2∙105 МПа. Дано: 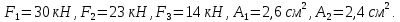 Решение           A2 A1  F3 F2 F1 F3 F2 F1V IV III II I       0,35 0,35 0,1 0,6 0,1 0,35 0,35 0,1 0,6 0,1  39 53 Эпюра N, 39 53 Эпюра N, 30 кН 30 кН 220,8 220,8  162,5 203,8 Эпюра 162,5 203,8 Эпюра 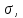  115,4 МПа 115,4 МПаРешение Определим значения продольных сил на участках стержня: 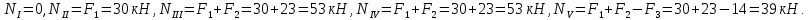 Определим значения нормальных напряжений для каждого участка: 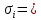 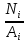 ; ;Тогда получим 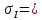 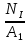 = = 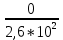 = 0; = 0; 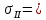 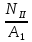 = = 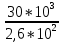 = 115,4 МПа; = 115,4 МПа;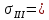 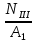 = = 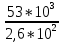 = 203,8 МПа; = 203,8 МПа; 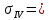 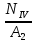 = = 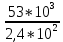 = 220,8 МПа; = 220,8 МПа;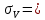 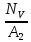 = = 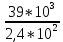 = 162,5 МПа. = 162,5 МПа.По результатам расчетов построены эпюры N и 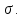 Изменение длины участков стержня определим по формуле Гука: 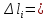 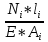 ; ;Отсюда имеем 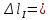 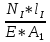 = = 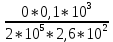 = 0; = 0; 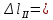 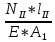 = = 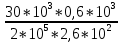 = 0,346 мм; = 0,346 мм;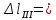 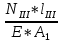 = = 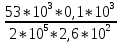 = 0,102 мм; = 0,102 мм; 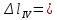 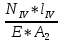 = = 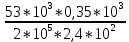 = 0,386 мм; = 0,386 мм; 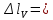 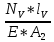 = = 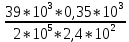 = 0,284 мм. = 0,284 мм.Определим перемещение свободного конца бруса: 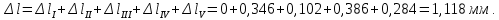 Ответ: 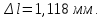 Задача 80 Конструкция, состоящая из трех стальных стержней, соединенных шарнирно, нагружена силой F. Все стержни имеют одну и ту же площадь поперечного сечения А. Принять [σ] = 160 МПа. Определить силы в стержнях и перемещение шарнира О. Дано: l = 1,5 м; 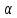 = 35°; F = 40 кН. = 35°; F = 40 кН.Решение  y y   RA RB RC RA RB RC                   A B C A B C 1 2 3 l l1   O O 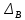 x x 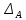  F Так как соединения всех концов стержней шарнирные, то реакции RA, RB и RC шарниров А, В и С направлены вдоль осей стержней и пересекаются в точке О. Число реакций равно трем, но т.к. система и нагрузка симметричные, то RA = RC (это вытекает из первого уравнения равновесия 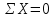 ). У нас имеется две неизвестные реакции и одно уравнение равновесия, следовательно, система один раз статически неопределимая. ). У нас имеется две неизвестные реакции и одно уравнение равновесия, следовательно, система один раз статически неопределимая.Уравнение равновесия 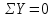 имеет вид: имеет вид: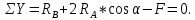 (1) (1)Для составления дополнительного уравнения рассмотрим перемещение системы. Стержень ВО под действием продольной силы RB удлинится на величину 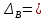 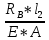 = = 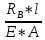 , ,где l2 = l – длина стержня ВО; A – площадь сечения стержня. Стержень АО под действием продольной силы RА удлинится на величину 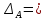 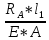 = = 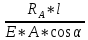 , ,где l1 = 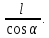 Шарнир О опустится на величину 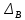 и займет положение и займет положение 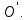 Тогда 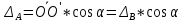 (2) (2)(Здесь принимаем 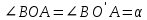 вследствие несущественного перемещения по сравнению с длиной стержней). вследствие несущественного перемещения по сравнению с длиной стержней).Подставив в уравнение (2) выражения 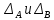 , получим , получим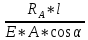 = = 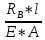 * *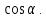 Отсюда 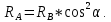 Решая совместно полученное уравнение с уравнением (1), найдем искомые величины RB = 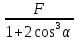 = = 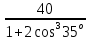 = 19,05 кН; = 19,05 кН; RA = RC = 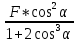 = = 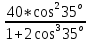 = 12,79 кН; = 12,79 кН; Определим площадь сечения стержня A = 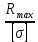 = = 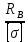 = = 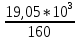 = 119,1 мм2. = 119,1 мм2.Принимаем А = 120 мм2. Определим перемещение шарнира О 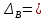 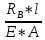 = = 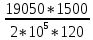 = 1,19 мм. = 1,19 мм.Ответ: 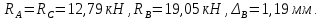 Задача 83 Для стального вала постоянного поперечного сечения: 1) определить значения моментов M1, М2, M3, М4; 2) построить эпюру крутящих моментов; 3) определить диаметр вала из расчетов на прочность и жесткость, приняв [τк] = 30 МПа; [ 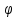 0] = 0,02 рад/м. Окончательно принимаемое значение диаметра вала должно быть округлено до ближайшего большего четного или оканчивающегося на пять числа. 0] = 0,02 рад/м. Окончательно принимаемое значение диаметра вала должно быть округлено до ближайшего большего четного или оканчивающегося на пять числа.Дано: 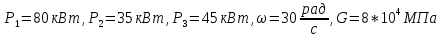 Решение Определяем внешние скручивающие моменты: M1 = 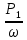 = = 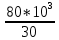 = 2667 Н*м; = 2667 Н*м;M2 = 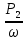 = = 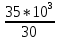 = 1167 Н*м; = 1167 Н*м;M3 = 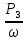 = = 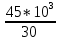 = 1500 Н*м. = 1500 Н*м.Определяем уравновешивающий момент M4: 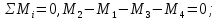 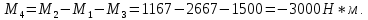 Действительное направление уравновешивающего момента M4 противоположно указанному в задании. На расчетной схеме (рис. 1) указываем действительное направление уравновешивающего момента M4. Определим значения крутящих моментов на участках вала 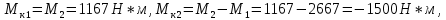 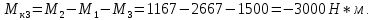 Строим эпюру крутящих моментов Мк (рис.1).                      М2=1167Н*м М1=2667Н*м М3=1500Н*м М4=3000Н*м М2=1167Н*м М1=2667Н*м М3=1500Н*м М4=3000Н*мI II III  1167 1167     1500 3000 Рис. 1. Схема нагружения вала и эпюра крутящих моментов Определяем диаметр вала из условий прочности и жесткости: Мкmax = 3000 Н*м. Из условия прочности |
