Решение а Аналитическое решение

• Название: Решение а Аналитическое решение
• Дата: 20.06.2021
• Размер: 484.07 Kb.
• Имя файла: 1673154433 (3).docx
• Тип: Задача; #219242
• страница: 2 из 3

Задача №4

Длинный металлический вал диаметром d, который имел температуру t₀ = 20 °С, был помещен в печь с температурой t_m = 820 °С.

Определить температуру t_rτ на расстоянии r = br₀ от оси вала че­рез τ минут после начала нагревания. Коэффициент теплоотдачи на поверх­ности вала α = 140 Вт/(м²·К). Диаметр вала, материал и коэффициент b приведены в таблице.

Исходные данные: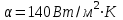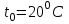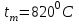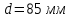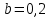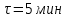

; ;

; ;

; ;

Латунь.

Решение:

Определяем физические параметры латуни:

- коэффициент теплопроводности λ =111 Вт/(м·К);

- коэффициент температуропроводности а = 0,34·10^-6 м²/с.

2. Вычисляем число Фурье: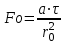

,

где r₀ – радиус вала;

τ – время нагрева, с.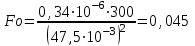



3. Вычисляем число Био: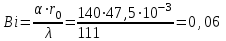



4. Определяем температуру на оси и на поверхности вала с помощью номограмм.

По графику для поверхности вала определяем безразмерную температуру поверхности вала Q_п = 0,8, по графику для центра вала определяем безразмерную температуру центра вала Q_ц = 0,90.

Относительная безразмерная температура поверхности.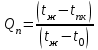

,

где t_пк – температура поверхности вала в конце нагрева, ⁰С;

t_ж – температура печи, ⁰С;

t₀ – начальная температура поверхности вала, ⁰С.

Отсюда получаем температуру поверхности в конце нагрева: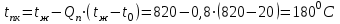



Получаем температуру в центре заготовки через 5 мин после начала нагрева: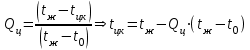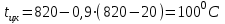





5.Определяем температуру на расстоянии r = 0,2r₀ = 0,2·47,5 = 9,5 мм от оси вала в конце нагрева.

Используем соотношение (так как Fo < 0,25, то для расчёта безразмерной температуры берём три члена ряда):

θ(r, τ) = 2J₁(μ₁)·J₀(μ₁·r/r₀)·exp(-μ₁²·Fo)/( μ₁[J₁²(μ₁) +J₀²(μ₁)] +

+2J₁(μ₂) ·J₀(μ₂·r/r₀) ·exp(-μ₂²·Fo)/( μ₂[J₁²(μ₂) +J₀²(μ₂)] +

+2J₁(μ₃) ·J₀(μ₃*r/r₀) ·exp(-μ₃²·Fo)/( μ₃[J₁²(μ₃) +J₀²(μ₃)].

Значение μ₁, μ₂, μ₃ в зависимости от величины числа Био принимаем по таблице: μ₁ = 1,5325; μ₂ = 4,5979; μ₃ = 7,6647.

При μ₁ = 1,5325 функции Бесселя: J₀=0,512; J₁ = 0,558.

При μ₂ = 4,5979 функции Бесселя: J₀=- 0,321; J₁ = -0,231.

При μ₃ = 7,6647 функции Бесселя: J₀=0,266; J₁ = 0,135.

μ₁·r/r₀ = 1,5325·0,0475/0,019 = 3,83→ J₀= - 0,38;

μ₂·r/r₀ = 4,5979·0,0475/0,019 = 12→ J₀= 0,048;

μ₃·r/r₀ = 7,6647·0,0475/0,019 = 19→ J₀= - 0,014.

θ(0,019м;25м)=2·0,558·(0,38)·exp(1,5325²·0,23)/(1,5325· [0,558²+0,512²]+

+2· (-0,231) · (0,048) ·exp(-4,5976²·0,23)/(4,5976· [(-0,231)²+(-0,321)²]+

+2·0,135· (-0,014) ·exp(-7,6647²·0,23)/(7,6647· [0,135²+0,266²] = 0,87.

Температура на расстоянии r = 0,2r₀ = 0,2·47,5 = 9,5 мм от оси вала в конце нагрева: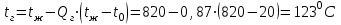



t_r = t_ж – Q_r*( t_ж – t₀) = 820 – 0,87*(820 – 20) = 123⁰С.
.

Задача №5

Рукавная линия с внутренним диаметром d поперечно обдувается ветром со скоростью w₂ . Температура воздуха t₂. По рукавной линии с расходом G₁ движется вода, температура которой на входе в рукавную ли­нию t₁^’. Рассчитать максимальную длину рукавной линии из условия, что температура воды на выходе из рукавной линии была бы t₁^’ ≥°С. Толщина стенки рукавной линии δ=2 мм. Эквивалентный коэффициент теплопро­водности материала рукава λ = 0,6 Вт(м·К).

Исходные данные: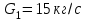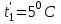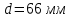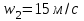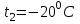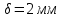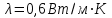

; ; ;

; ; ;



Найти:

1.Определяем среднюю температуру воды в рукаве.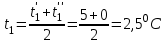



При t₁ = 2,5⁰С для воды:

- кинематический коэффициент вязкости ν₁= 1,644·10^-6 м²/с;

- коэффициент теплопроводности λ₁ = 55,7·10^-2 Вт/(м*К);

- удельная изобарная массовая теплоемкость С_р1 = 4,206 кДж/(кг·К);

- плотность ρ₁ = 999,8 кг/м³;

- коэффициент объёмного расширения β = 0,4·10^-4 К^-1;

- число Прандтля Pr₁ = 12,43.

2. Определяем режим движения воды, вычислив число Рейнольдса.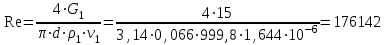



3.Определяем число Нуссельта.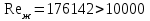

(развитое турбулентное течение воды) и число Нуссельта рассчитывается по уравнению: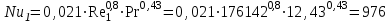



4. Коэффициент теплоотдачи от воды к внутренней поверхности рукава.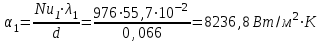



5. Определяем физические свойства воздуха.

При t₂ = -20⁰С для воздуха:

- кинематический коэффициент вязкости ν₂ = 11,61·10^-6 м²/с;

- коэффициент теплопроводности λ₂ = 2,28·10^-2 Вт/(м·К);

- число Прандтля Pr₂ = 0,716.

6. Определяем режим движения воздуха, вычислив число Рейнольдса.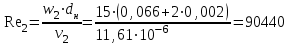



7. Определяем число Нуссельта.

При 10³ < Re_в < 2·10⁵ число Нуссельта рассчитывается по уравнению: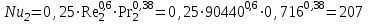



8. Определяем коэффициент теплоотдачи от поверхности рукава к воздуху.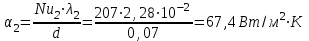



9.Определяем коэффициент теплопередачи от воды, движущейся по рукаву, к воздуху.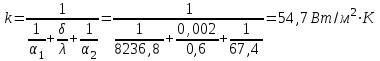



10. Определяем максимальную длину рукавной линии.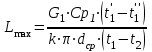



где d_ср = d + δ = 0,066 + 0,002 = 0,068 м - средний диаметр рукава.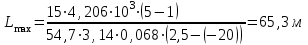


Задача № 6

Для подогрева воды выхлопными газами в цистерне пожарного авто­мобиля смонтирован горизонтальный трубопровод, наружный диаметр ко­торого d. Определить длину трубопровода, необходимую для компенсации тепловых потерь от воды через стенку цистерны в окружающую среду, ес­ли принять, что диаметр цистерны D, ее длина L, температура окружающе­го воздуха t_в, температура воды в цистерне t_ж, температура стенки трубо­провода t_c. Термическим сопротивлением стенки цистерны пренебречь, а температуру стенки принять равной температуре воды в цистерне. Данные, необходимые для расчетов, приведены в таблице.

Исходные данные: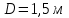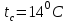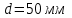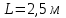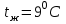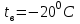

; ; ;

; ; ;

Найти:
Решение:

1.Определяем теплофизические характеристики воды при t_ж = 9⁰C.

- кинематический коэффициент вязкости ν_ж= 1,306·10^-6 м²/с;

- коэффициент теплопроводности λ_ж = 57,4·10^-2 Вт/(м*К);

- коэффициент объёмного расширения β_ж = 0,7·10^-4 К^-1;

- число Прандтля Pr_ж = 9,52;

- число Прандтля при t_С = 14⁰C Pr_с = 7,79.

2. Определяем величину безразмерного комплекса (Gr·Pr)_ж.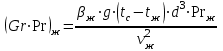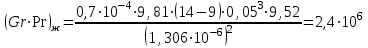





3. Определяем число Нуссельта.

При 10³ < (Gr·Pr)_ж.<10⁹ число Нуссельта рассчитывается по уравнению: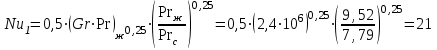



4. Определяем коэффициент теплоотдачи от поверхности трубопровода к воде в цистерне.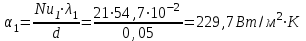



5. Определяем теплофизические характеристики воздуха при t_В= - 15⁰C.

- кинематический коэффициент вязкости ν_В= 12,11·10^-6 м²/с;

- коэффициент теплопроводности λ_В = 2,32·10^-2 Вт/(м·К);

- число Прандтля Pr_В = 0,714;

- коэффициент объёмного расширения β_В =1/Т_В = 1/258 К^-1.

6. Определяем величину безразмерного комплекса (Gr·Pr)_в.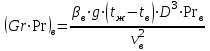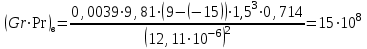





7. Определяем число Нуссельта.

При 10³ <(Gr·Pr)_В <10⁹ число Нуссельта рассчитывается по уравнению: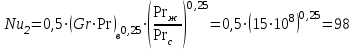



8. Определяем коэффициент теплоотдачи от поверхности цистерны к окружающему воздуху.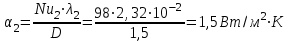



9. Вычисляем длину трубопровода.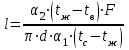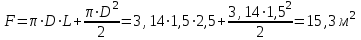

,

– площадь поверхности цистерны.


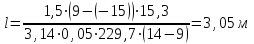Задача № 7

Определить минимальное расстояние, обеспечивающее безопасность
соседнего с горящим объекта, при следующих исходных данных: проекция
факела пламени горящего объекта имеет прямоугольную форму размером
dх l; температура факела равна Т_ф; а степень черноты – ε_ф. Для не горящего
объекта: допустимое значение температуры на поверхности равно Т_доп; допустимое значение плотности теплового потока (критическая плотность) -
q_кр; степень черноты поверхности - ε. Кроме того, оценить безопасное расстояние от факела до личного состава, работающего на пожаре без средств защиты от теплового воздействия, при условии кратковременного пребывания и длительной работы.

При кратковременном тепловом воздействии для человека при­нять q_кр = 1120 Вт/м²; при длительном - q_кр = 560 Вт/м². При решении зада­чи учитывать только теплообмен излучением. Коэффициент безопасности, принять равным β. Данные для расчета выбрать из таблицы.

Исходные данные: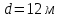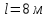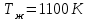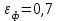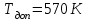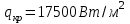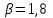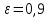

; ; ;

; ; ;

;

Решение:

Приведенная степень черноты: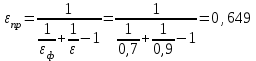



Условие тепловой устойчивости: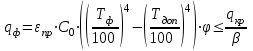



Отсюда требуемый средний коэффициент облучаемости: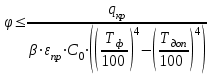



Учитывая, что φ = 4φ₁₂, получаем: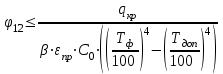



Функция φ12 описывается формулой: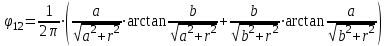


где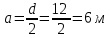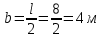



а) Для поверхности негорящего объекта q_кр=17500 Вт/м²: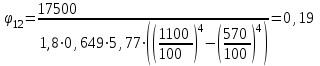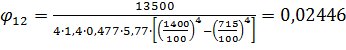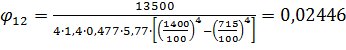


.
Решим уравнение φ12=0,024 относительно r методом последовательных приближений:

r, м
φ12

Т.о. получаем r=

б) Для кратковременного пребывания людей qкр=1120 Вт/м2:

Вт/м2.

r, м
φ12

Т.о. получаем r=

в) Для длительного пребывания людей qкр=560 Вт/м2: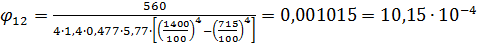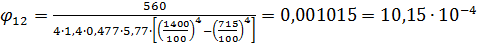
Вт/м2.

r, м
φ12

Т.о. получаем r=


Пояснения к решению задачи № 7
Условия безопасности, будут соблюдаться тогда, когда результирующая плотность теплового потока излучением между факелом и поверх­ностью соседнего объекта q_фп будет меньше допустимого значения q_кр.

Сучетом коэффициента безопасности получим:

βq_фп≤ q_кр.

Результирующая плотность теплового потока между факелом и поверхностью тела рассчитывается по формуле: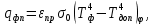



где 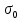=5,7·10^-8, Вт/(м²·К⁴) - константа излучения абсолютно черного тела;

ε_пр - приведенная степень черноты системы факел- поверхность, ;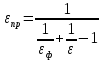

φ – средний по поверхности полный коэффициент облученности.
Значения φ₂₁ для одной четвертой греющей поверхности рассчитываются по формуле:

φ₂₁=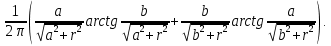

Средний по поверхности полный коэффициент облученности φ=4φ₂₁;

а, b- стороны прямоугольника, а=d/2, b=l/2;

r- расстояние ме­жду факелом и поверхностью облучаемого объекта.

Минимальное безопасное расстояние следует находить при соблюдении условий:

φ=2φ₂₁; а=d, b=l; βq_фп= q_кр.