Контрольная работа по теме Пределы вариант 10. контрольная работа по теме Пределы вариант 10. Решение а б Найдем аналитические координаты вектора
 Скачать 456.5 Kb. Скачать 456.5 Kb.
|
|
Контрольная работа, вариант 10. Задание 1. Даны точки 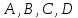 : :а) построить вектор 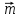 и разложить его в базисе ( и разложить его в базисе ( ; ;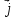 ); );б) найти аналитические координаты вектора 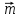 . Сравнить результаты с полученными в пункте а; . Сравнить результаты с полученными в пункте а;в) составить общее уравнение прямой, проходящей через точку А, перпендикулярно вектору  . .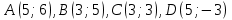 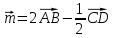 Решение. а) 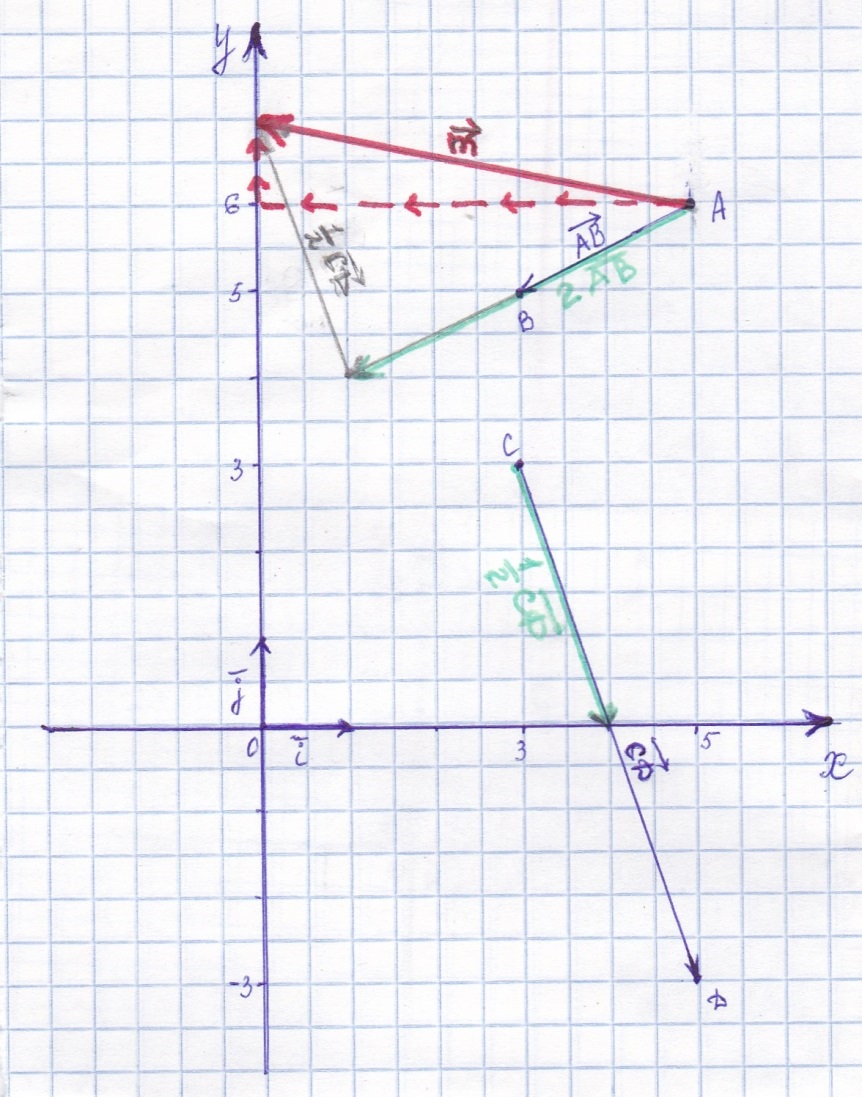 б) Найдем аналитические координаты вектора 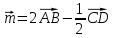 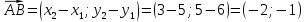 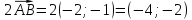 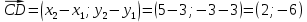 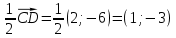 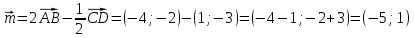 Аналитический способ решения привел к тем же результатам, что и графический. в) 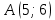 ; ; 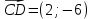 Найдем уравнение прямой по точке и вектору нормали, которое задается формулой  Составим при А=2, В=  6 уравнение прямой: 6 уравнение прямой: 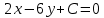 . .Для нахождения коэффициента С подставим координаты точки в полученное выражение: 2∙5  6∙ 6+С=0 6∙ 6+С=010  36+С=0 36+С=0 26+С=0 26+С=0С=26 Искомое уравнение прямой имеет вид: 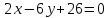 Ответ:  Задание 2 Найти пределы: а) 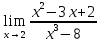 ; б) ; б) 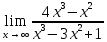 Решение. а) 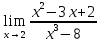 При непосредственной подстановке числа 2 в функцию получим неопределенность вида 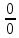 , т.к. , т.к. 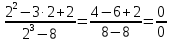 . .Разложим числитель и знаменатель на множители: 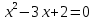 находим дискриминант D=b2  4ac=9 4ac=9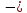 4∙2=1 4∙2=1находим корни x1= 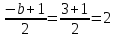 ; х2= ; х2=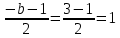 т.обр. 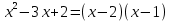 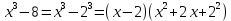 Получаем: 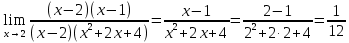 Ответ: 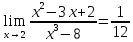 б) 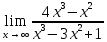 Решение. Разделим числитель и знаменатель на старшую степень 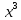 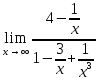 Т.к. 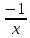 , , 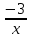 и и 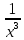 стремятся к 0, то получим стремятся к 0, то получим 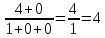 . .Ответ: 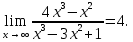 Задание 3. 3.1 Найти производную заданной функции: 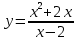 Решение. Применяем правило дифференцирования частного 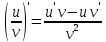 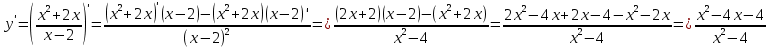 Ответ: 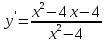 3.2 Исследовать функцию на экстремумы и интервалы монотонности: 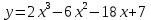 Решение. а) Функция определена и непрерывна на всей числовой прямой. б) Находим критические точки 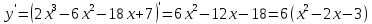 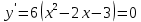 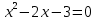 D= b2  4ac=4 4ac=4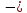 4∙( 4∙(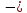 3)=16 3)=16x1= 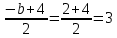 x2=  в) Проверяем достаточное условие экстремума 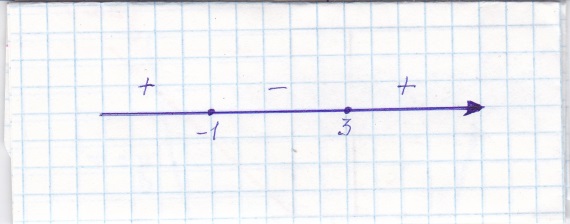 Определяем знаки производной: на интервале ( 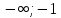 ), возьмем произвольную точку интервала, подставив в производную, получим ), возьмем произвольную точку интервала, подставив в производную, получим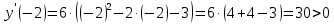 а значит, функция положительна и в каждой точке интервала (функция возрастает); на интервале ( 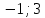 ), возьмем произвольную точку интервала, подставив в производную, получим ), возьмем произвольную точку интервала, подставив в производную, получим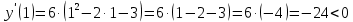 а значит, функция отрицательна и в каждой точке интервала (функция убывает); на интервале ( 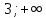 ), возьмем произвольную точку интервала, подставив в производную, получим ), возьмем произвольную точку интервала, подставив в производную, получим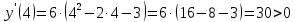 а значит, функция положительна и в каждой точке интервала (функция возрастает); г) При переходе через точку х= 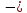 1 производная меняет знак с «+» на « 1 производная меняет знак с «+» на «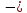 » и функция достигает максимума: » и функция достигает максимума: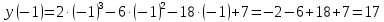 При переходе через точку х=3 производная меняет знак с « 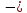 » на «+» и функция достигает минимума: » на «+» и функция достигает минимума: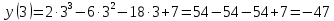 Ответ: функция возрастает на интервалах ( 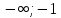 ), ( ), (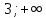 ) и убывает на интервале ( ) и убывает на интервале (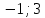 ); в точке х= ); в точке х=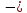 1 функция достигает максимума: у( 1 функция достигает максимума: у(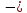 1)=17, а в точке х=3 – минимума: у(3)= 1)=17, а в точке х=3 – минимума: у(3)=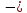 47. 47. Задание 4. Взять неопределенный интеграл методом прямого интегрирования: 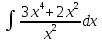 Решение. Перепишем подынтегральное выражение: 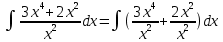 Упростим выражение 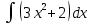 Интеграл суммы функций равен сумме интегралов от каждой функции в отдельности 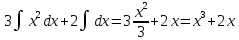 Ответ: 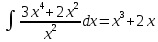 . .Задание 5. Вычислить площадь фигуры, ограниченной заданными линиями (чертеж обязателен):  Решение.   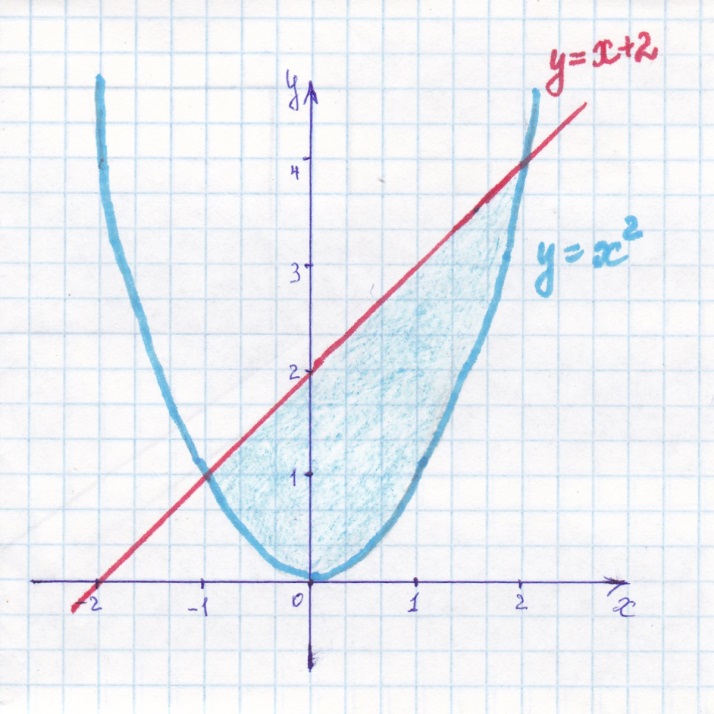 Найдем точки пересечения заданных линий. Для этого решим систему уравнений: 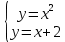 Для нахождения абсцисс точек пересечений заданных линий решим уравнение: 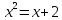 или или 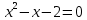 . Находим корни: . Находим корни:D= b2 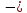 4ac= 4ac= 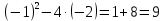 x1= 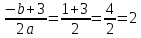 x2= 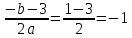 Данные линии, представляющие собой параболу и прямую, пересекаются в точках 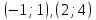 . Эти линии образуют замкнутую фигуру, площадь которой вычисляется по формуле: . Эти линии образуют замкнутую фигуру, площадь которой вычисляется по формуле: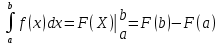 Подставляем значения: 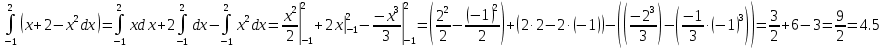 Ответ: 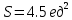 Задание 6. Решить систему линейных уравнений методом Крамера: 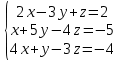 Решение. Найдем определитель системы: 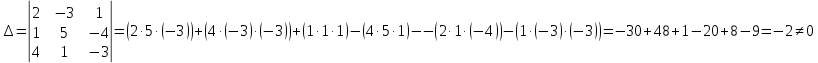 Определитель не равен 0, следовательно, система является определенной. Для нахождения её решения вычислим определители при неизвестных: 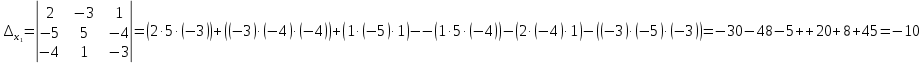 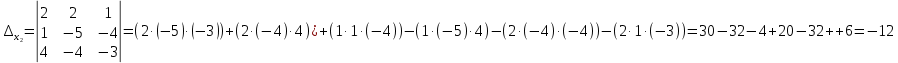  По формулам Крамера найдем: 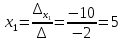  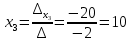 Ответ: 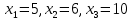 |
