Курсовая по информатике______________. Исследование численных методов вычисления определенных интегралов

• Название: Исследование численных методов вычисления определенных интегралов
• Анкор: Исследование численных методов вычисления определенных интегралов
• Дата: 17.04.2022
• Размер: 1.28 Mb.
• Имя файла: Курсовая по информатике______________.docx
• Тип: Исследование; #480509
• страница: 1 из 3

Государственное образовательное учреждение

высшего профессионального образования

«Тверской государственный технический университет»

(ГОУВПО «ТвГТУ»)

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   Кафедра информатики и прикладной математики
   

Курсовая работа
по дисциплине "Информатика"

на тему: Исследование численных методов вычисления определенных интегралов

Выполнил(а): студент(ка) группы Б.ТТ.АЭС.21.04

Фамилия (инициалы): Исаченко М.С.

Номер зачетной книжки:

Проверил: Ганичев А.В.

Тверь, 2021

СОДЕРЖАНИЕ

Оглавление

5. 
   Введение
   

При решении ряда актуальных физических и технических задач встречаются определенные интегралы от функций, первообразные которых не выражаются через элементарные функции. Кроме того, в приложениях приходится иметь дело с определенными интегралами, сами подынтегральные функции которых не являются элементарными. Это приводит к необходимости разработки приближенных методов вычисления определенных интегралов.

Цель работы:

выработать навык использования табличного процессора MS Excel для численного (приближенного) вычисления определенных интегралов (интегрирование) заданных в табличном виде.

Задачи:

1) вычислить определенный интеграл с заданной точностью ε методами: правых прямоугольников, центральных прямоугольников, левых прямоугольников, трапеций, Симпсона. Сравнить полученные результаты, сделать выводы;

2) вычислить значение интеграла аналитически;

3) исследовать зависимость точности вычисления интеграла ε от числа шагов n (точность – это модуль разности между численным и аналитическим значением)

Сравнить полученные результаты, сделать выводы;

4) оценить погрешность вычисления интеграла по правилу Рунге;

5) для наглядности полученных результатов использовать таблицы и графики;

6. 
   1. Численное интегрирование.
   

1.1. Постановка задачи.
Пусть требуется вычислить определенный интеграл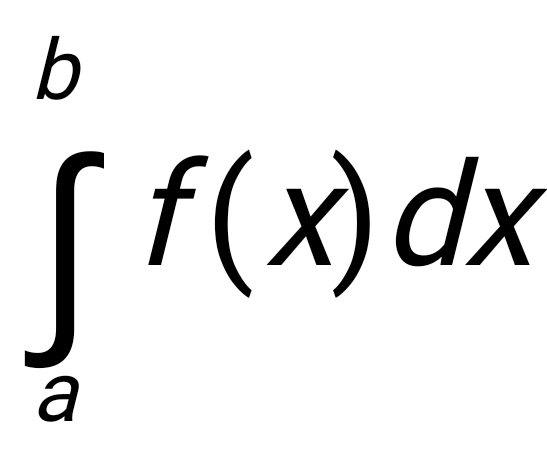

, (1)

где f(x) – непрерывная на отрезке [a; b] функция.

С геометрической точки зрения интеграл (1) при f(x)> 0 равен площади криволинейной трапеции, ограниченной кривой y = f(x), осью Ox и прямыми x = a, x = b (рис. 1). Другими словами, 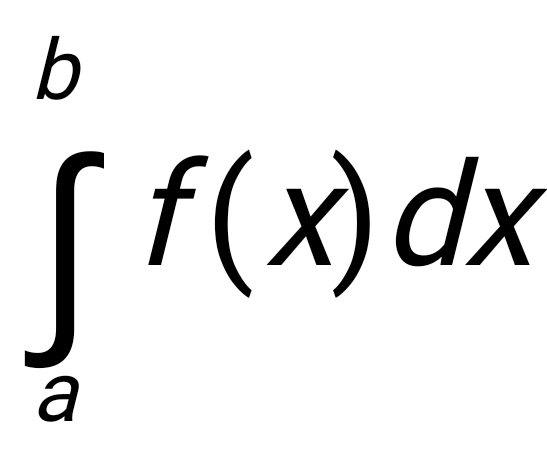равен площади заштрихованной фигуры на рис. 1.

Рис. 1. Геометрический смысл определенного интеграла.
Вычислить определенный интеграл (1) можно с помощью аналитической формулы Ньютона-Лейбница 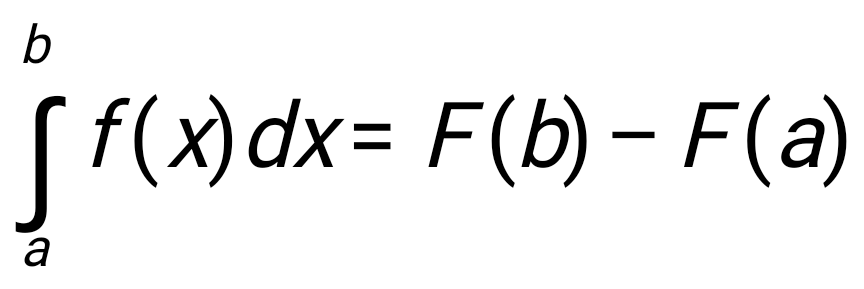(2):

, (2)

где F(x) – первообразная функция для заданной функции f(x).

Однако во многих случаях не удается найти никакой аналитической формулы в виду невозможности определения F(x).

Таким интегралом, например, является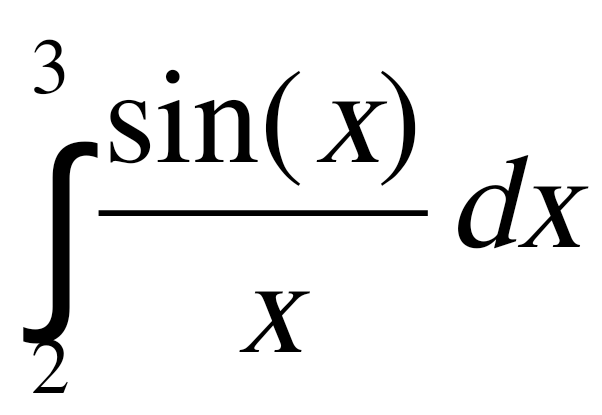

. (3)

В математическом анализе доказывается, что для данной подынтегральной функции нельзя выразить первообразную F(x) через элементарные функции. С другой стороны, площадь криволинейной трапеции, задаваемой интегралом (3) существует (рис. 3). Значит, должно существовать и значение интеграла, которое, однако, мы не можем найти точно.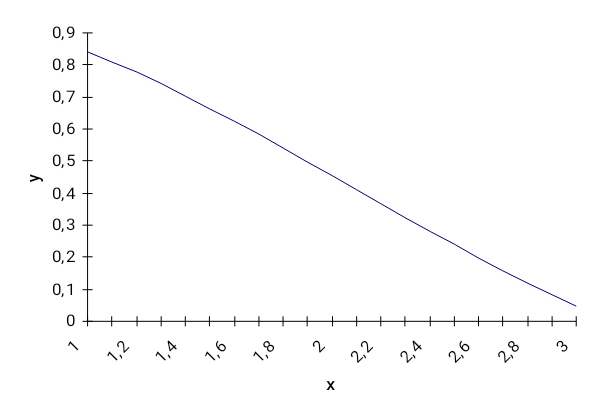



Рис. 2. График функции на отрезке [1; 3].

В таких случаях приходится применять методы численного интегрирования.

Основной принцип построения всех приближенных формул численного интегрирования состоит в том, что интервал интегрирования разбивается на множество меньших отрезков, внутри которых подынтегральная кривая y = f(x) заменяется с некоторой степенью точности более простыми функциями, интегралы от которых можно вычислить. С геометрической точки зрения выполняется следующее: искомая площадь криволинейной трапеции приближенно заменяется суммой площадей элементарных геометрических фигур.

1.2. Метод прямоугольников.

Как говорилось выше, вычисление интеграла 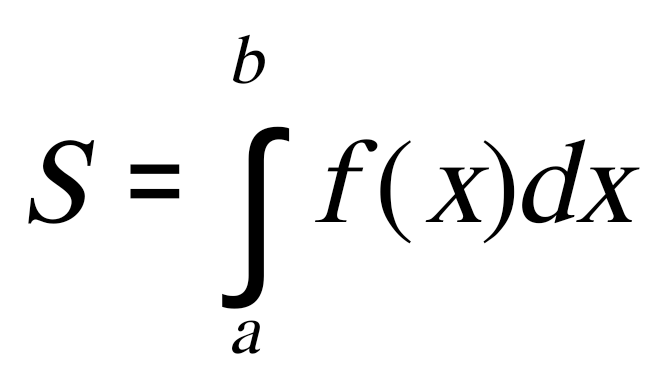равносильно вычислению площади некоторой фигуры – криволинейной трапеции с параллельными «основаниями» x = a, x = b и «боковыми сторонами» y = 0, y = f(x) (рис. 1).

Разобьем интервал интегрирования на n равных частей, каждая длиной .

Приближенное значение интеграла получается в виде суммы площадей n прямоугольников, высота которых равна значению f(x) на левом краю каждого подинтервала (рис. 3).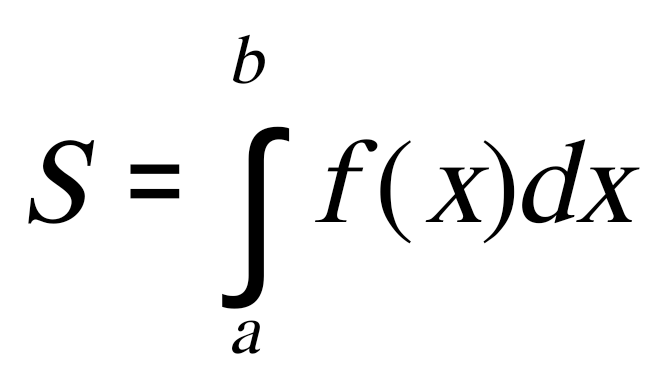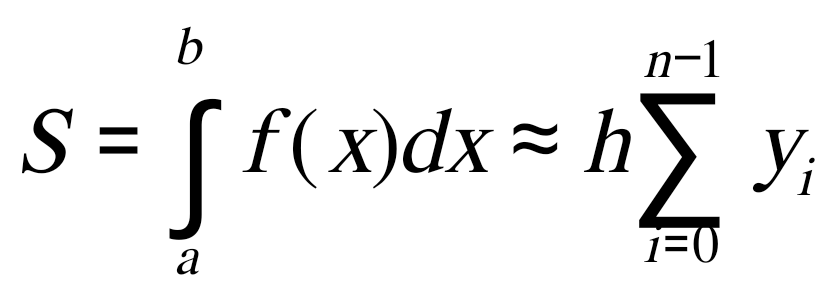

hy₀+hy₁+…+hy_n-1 = h(y₀+y₁+…+y_n-1). То есть формула численного интегрирования имеет вид:

(4)

и называется формулой «левых» прямоугольников.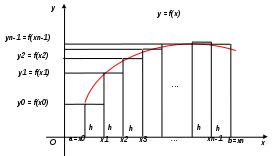

Рис. 3. Геометрическая интерпретация метода «левых» прямоугольников.
Если в качестве приближенного значения площади для каждого подинтервала принять площадь прямоугольника, высота которого равна значению f(x) на правом краю подинтервала (рис. 4), то формула численного интегрирования имеет вид 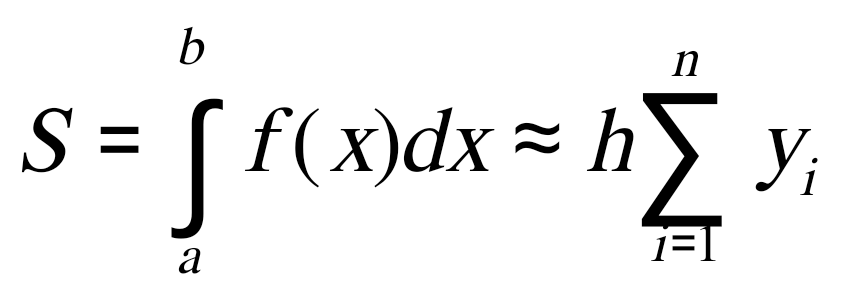(5):

(5)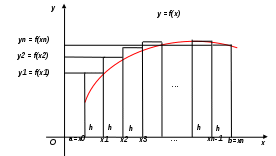


и называется формулой «правых» прямоугольников.

Рис. 4. Геометрическая интерпретация метода «правых» прямоугольников.
Существует третья модификация метода прямоугольников – метод «средних» прямоугольников. В этом случае в качестве приближенного значения площади для каждого подинтервала принимается площадь прямоугольника, высота которого равна значению f(x) в средней точке подинтервала (рис. 5).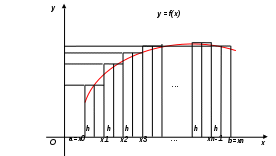

Рис. 5. Геометрическая интерпретация метода «средних» прямоугольников.
Тогда формула численного интегрирования имеет вид 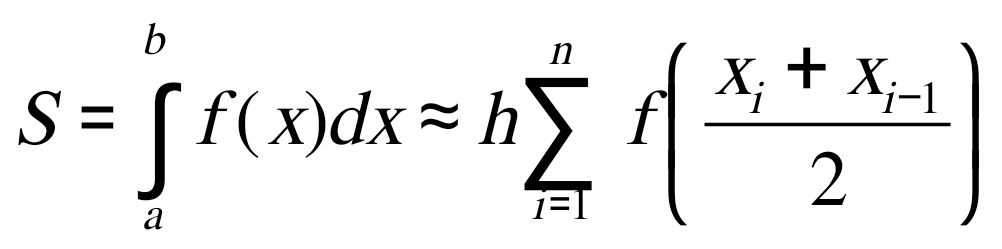(6):

(6)

Метод прямоугольников – это наиболее простой и вместе с тем наиболее грубый метод приближенного интегрирования. Очевидно, что чем больше будет число n отрезков разбиения, тем более точный результат дадут формулы (4)-(6). Однако увеличение числа отрезков разбиения промежутка интегрирования не всегда возможно. Поэтому большой интерес представляют формулы, дающие более точные результаты при том же числе точек разбиения. Заметно меньшую погрешность дает другой метод – метод трапеций.

1.3. Метод трапеций.

В этом методе отрезок [a; b] так же разбивается на n равных частей. На каждом отрезке [x_i; x_i+1] кривая y = f(x) заменяется прямой, проходящей через две известные точки с координатами 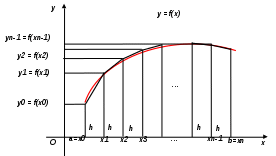и , где и строится прямоугольная трапеция с высотой (рис. 6).





Рис. 6. Геометрическая интерпретация метода трапеций.
В итоге искомая площадь криволинейной трапеции приближенно заменяется суммой площадей элементарных геометрических трапеций. (Площадь трапеции с высотой h и основаниями a, b вычисляется по формуле: ). Из гео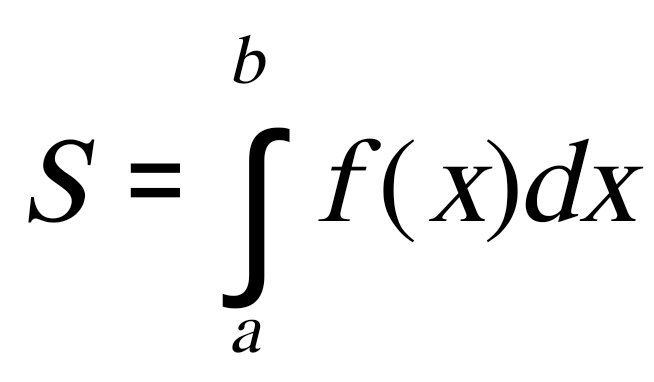метрических соображений понятно, что площадь такой фигуры будет, вообще говоря, более точно выражать площадь криволинейной трапеции, нежели площадь ступенчатой фигуры, рассматриваемая в методе прямоугольников.

Тогда



вынесем h за скобку, получим



разобьем каждую дробь на две дроби



приведем подобные слагаемые, получим

.

Итак, .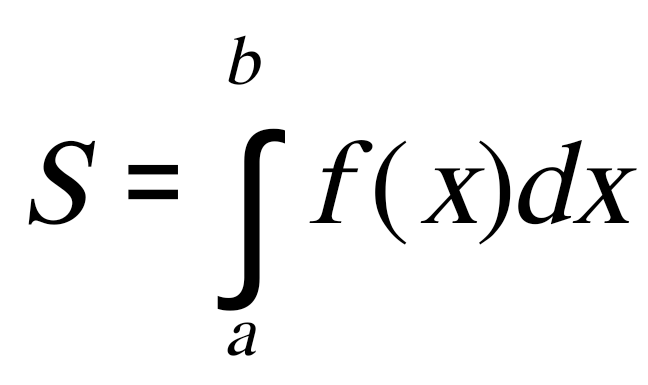

Коротко полученную формулу можно записать в виде (7).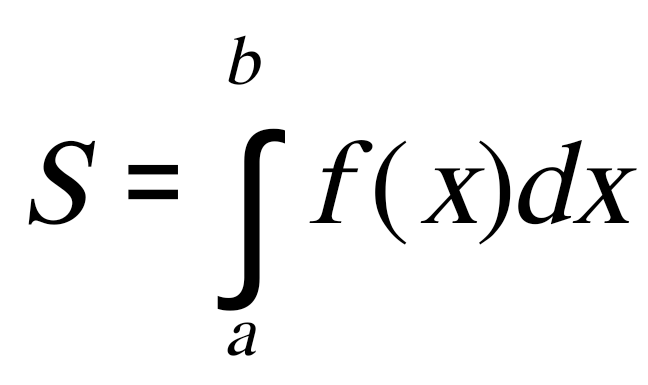

(7)

Заметим, что в данном методе получаем ступенчатую фигуру, составленную из трапеций, которая «плотнее» прилегает к заданной криволинейной трапеции, нежели фигура, составленная из прямоугольников в предыдущем методе.