Курсовая по информатике______________. Исследование численных методов вычисления определенных интегралов
 Скачать 1.28 Mb. Скачать 1.28 Mb.
|
Пример. Вычислить 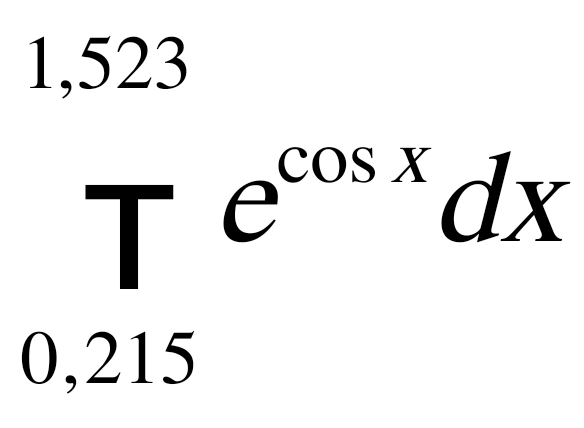 с точностью ε = 0,001 по методу Симпсона. с точностью ε = 0,001 по методу Симпсона.Решение. Оценим величину шага h по формуле (12): Выберем 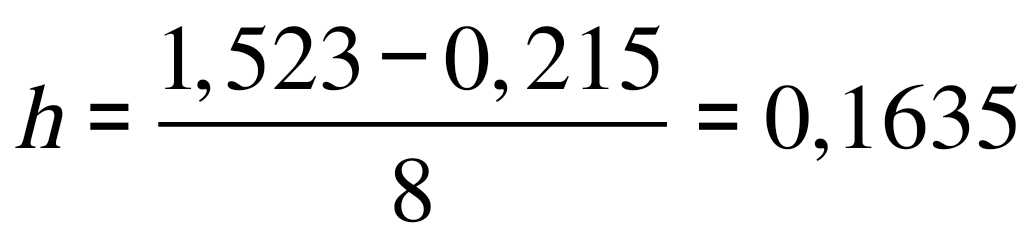 . (Заметим, что все промежуточные расчеты выполняем с запасной цифрой после запятой: так как точность ε = 0,001, то в вычислениях оставляем четыре цифры после запятой). . (Заметим, что все промежуточные расчеты выполняем с запасной цифрой после запятой: так как точность ε = 0,001, то в вычислениях оставляем четыре цифры после запятой).Используя формулу метода Симпсона, получаем 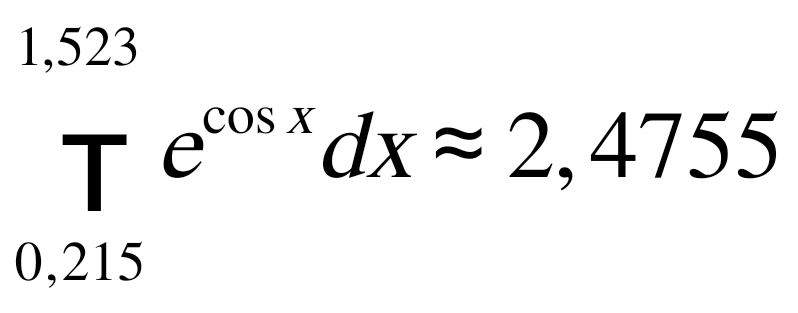 . .Проведем контроль точности вычислений по методу Рунге. Обозначим найденное значение интеграла с шагом 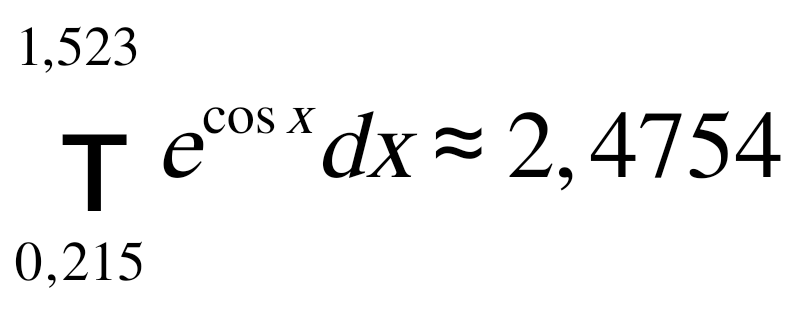 . .По формуле (13) имеем 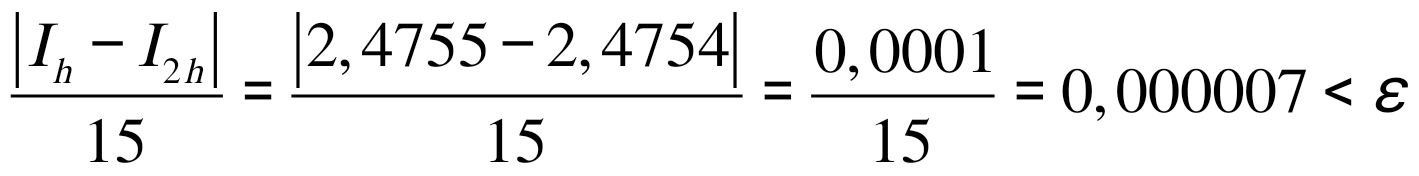 . .Условие (13) выполнено, следовательно, приближенное значение интеграла с точностью 0,001 равно 2. Практическая часть 2.1 Методика выполнения лабораторной работы Вычисление определенных интегралов Задание. Для примера своего варианта, используя MS Excel, вычислить определенный интеграл тремя способами: правостороннее приближение, левосторонние приближение и по формуле трапеций. Провести анализ вычислений для всех способов. Сделать выводы. Методика выполнения задания. Наиболее простое и в большинстве случаев приемлемое приближение состоит в том, что на каждом из интервалов, на которые разбит диапазон интегрирования, интегрируемая функция считается постоянной. В этом случае говорят о вычислении интеграла по формуле прямоугольников. При этом можно в качестве значения функции на интервале брать либо значение на правой границе интервала (правостороннее приближение), либо значение на левой границе интервала (левостороннее приближение). Ситуация проиллюстрирована на рисунках. Если все интервалы имеют одинаковую длину h, формулы имеют вид Это три основные формулы, позволяющие вычислять интегралы от функций, заданных в виде таблицы. Далее рассмотрим, как описанные методы могут использоваться для вычисления интегралов на практике.  Пример. Пример. Вычислить интеграл 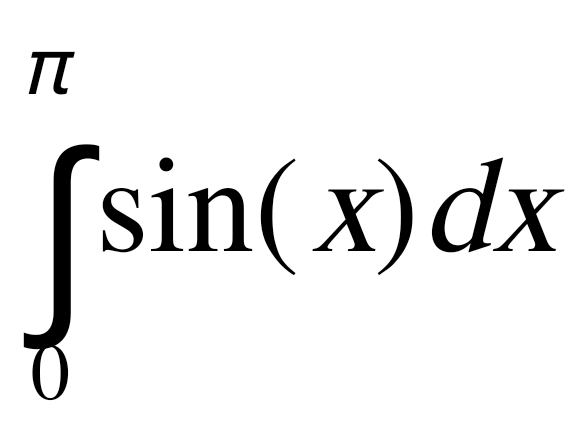 . .Этот интеграл может быть вычислен аналитически. В частности, очевидно, что 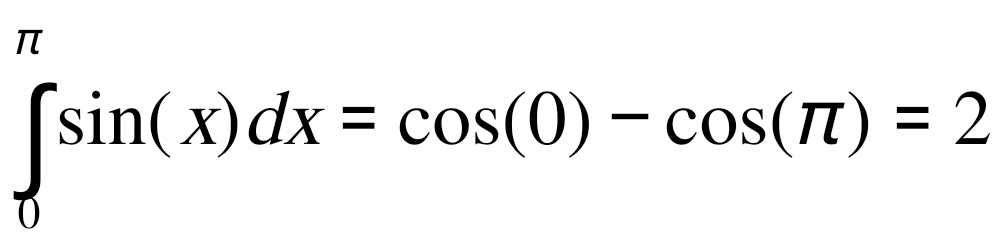 Именно это значение и попытаемся получить в результате интегрирования с использованием численных методов. 1. Оформляем таблицу, как показано на рисунке. 2. В ячейку А4 вводим число 0 как начальное значение для переменного интегрирования. После этого в ячейку А5 вводится формула =А4+ПИ()/10, согласно которой значение последующего узла получается прибавлением к предыдущему узлу десятой части от длины диапазона интегрирования (команда ПИ()/10) и копируем ее до А14. 3. В ячейку В4 вводим заданную формулу =SIN(A4) и копируем ее до ячейки В14. 4. Вводим формулы для вычисления площадей элементарных (базовых) прямоугольников или трапеций. В ячейку С4 вводим формулу =(А5 −А4)*В5 (правосторонние приближение), в ячейку D4 вводим практически такую же формулу =(А5−А4)*В4 (левосторонние приближение), и для метода трапеций в ячейку Е4 вводится формула =(А5−А4)*(В5+В4)/2. Заполнять данные для элементарных площадей следует вплоть до предпоследней строки диапазона (т.е. ячейки С14, D14, Е14 заполнять не следует — для этих ячеек введенные ранее формулы определения элементарных площадей не работают). Осталось только вычислить сумму значений в столбцах С, D и Е. Для этого выделяем ячейку С15 и вводим туда формулу =СУММ(C4:C13). В ячейку D15 вводится формула =СУММ(D4:D13), а в ячейку Е15 — формула =СУММ(E4:E13). Окончательный результат показан на рисунке. Результат вычислений для всех методов одинаковый. Абсолютная точность: |2−1,9835| = 0,0165. Относительная точность: 0,0165 / 1,9835 = 0,0083. 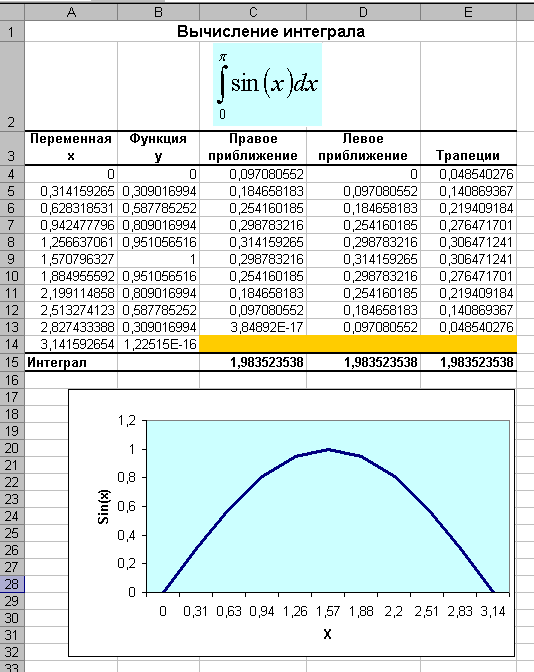 2.2 Вычисление интеграла 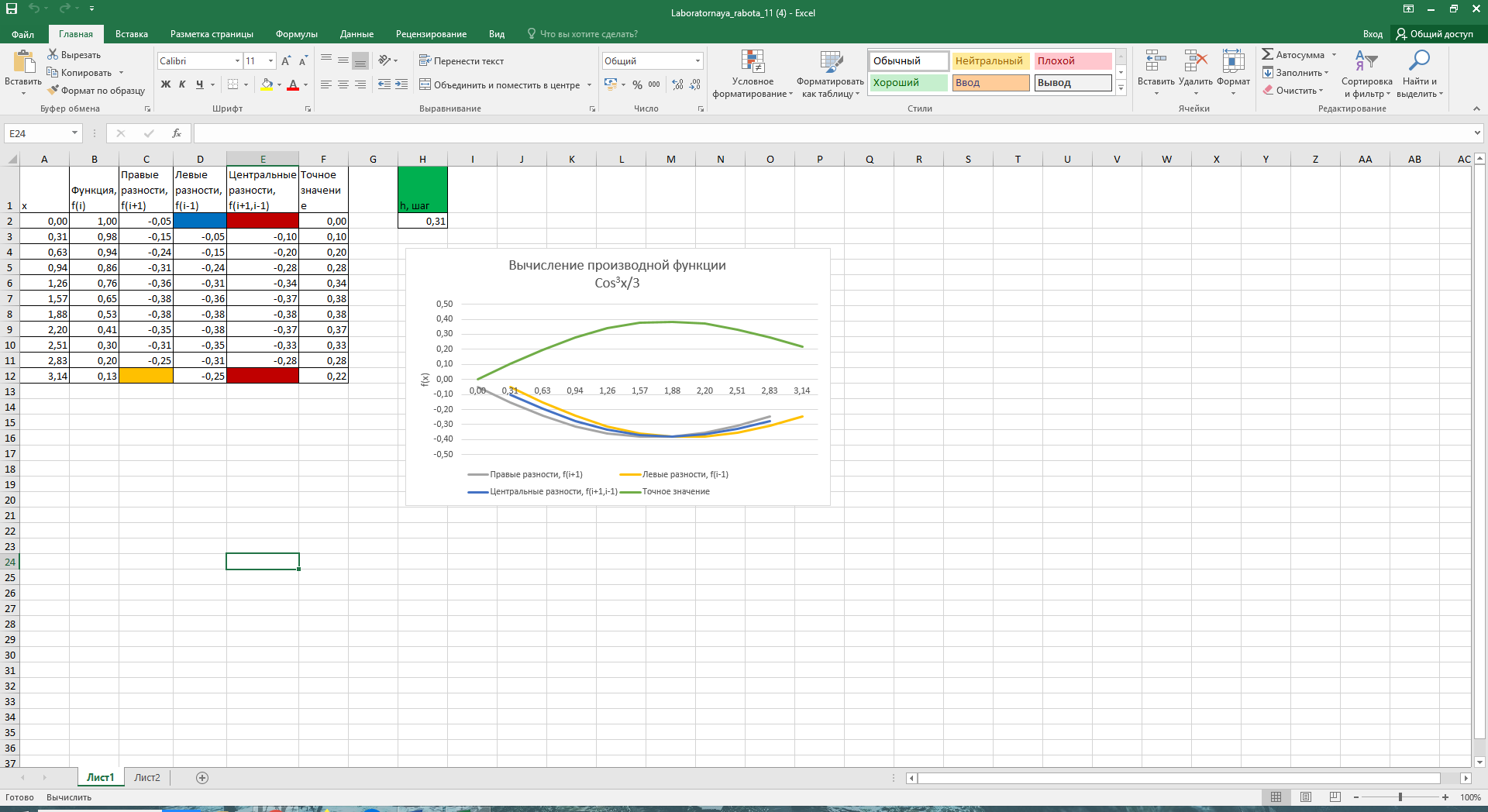 Рис 8. Вычисление производной функции Cos3x/3 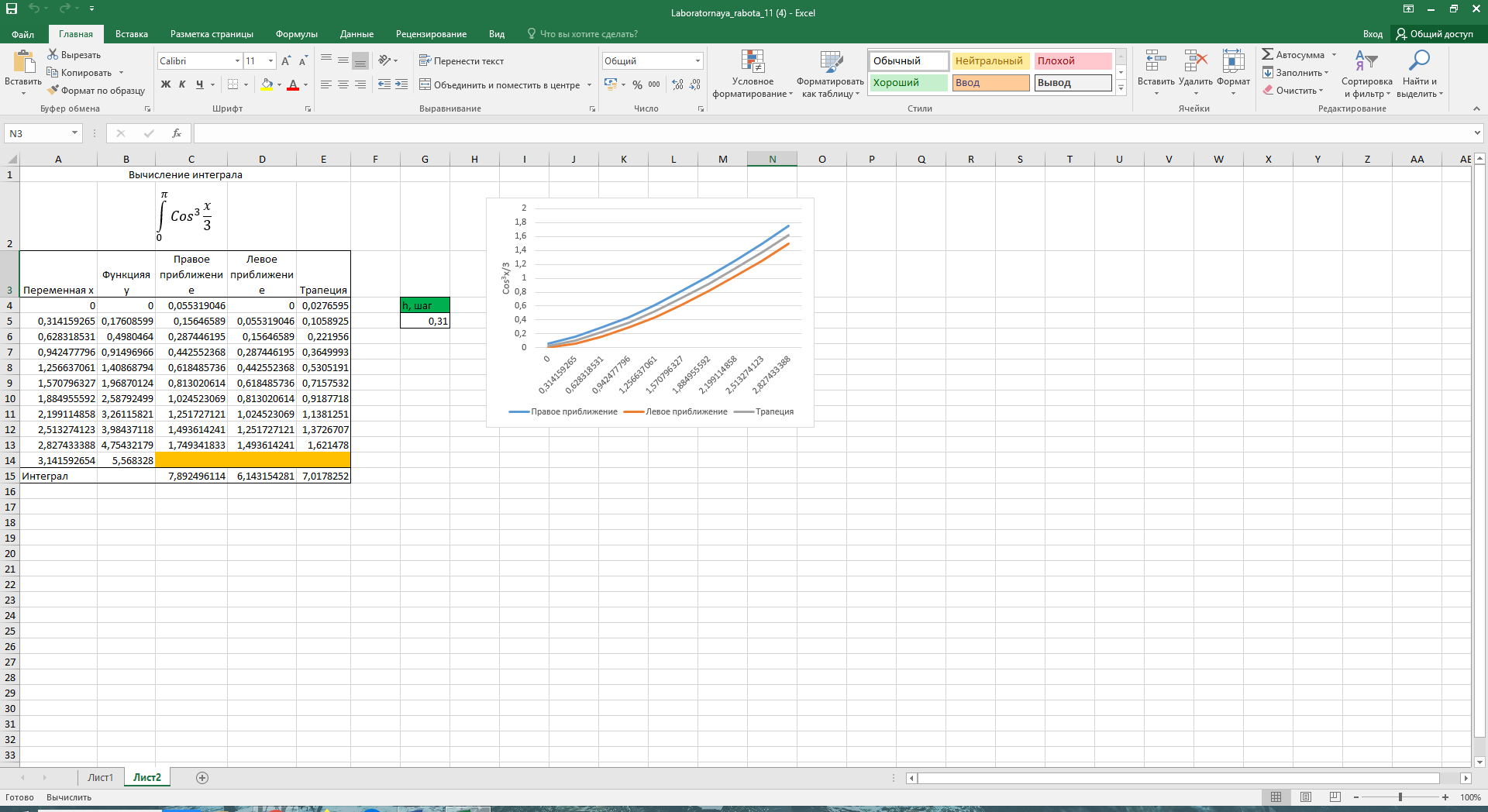 Рис 9. Вычисление интеграла Cos3x/3 Заключение В завершении работы, хочется отметить ряд особенностей применения рассмотренных выше методов. Каждый способ приближённого решения определённого интеграла имеет свои преимущества и недостатки, в зависимости от поставленной задачи следует использовать конкретные методы. Если необходимо быстро получить решение, но нет необходимости в большой точности ответа, следует воспользоваться одним из методов прямоугольника. Если же необходимо получить наиболее точный результат, идеально подходит метод Симпсона. Метод трапеций даёт ответ более точный, чем метод прямоугольников, но методу Симпсона он сильно уступает, этот метод можно назвать «золотой серединой» между двумя другими. Можно повысить точность вычисления увеличивая шаг интегрирования. Так же очень важны аналитические способы нахождения определенного интеграла, но они не всегда выполнимы, т.к. не всегда можно найти первообразную функции. Список литературы Волков Е. А. Численные методы.М., Высшая школа, 1990. Пискунов Н. С. Дифференциальное и интегральное исчисление. М. Гусак А.А. Высшая математика: Учеб. пособие для студентов вузов: В 2 т. - Мн., 1998. - 544 с. (1 т.), 448 с. (2 т.). Гусак А.А. Математический анализ и дифференциальные уравнения. - Мн.: ТетраСистемс, 1998. - 416 с. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч. I. - М.: Наука, 1982. - 616 с. |
