Курсовая по информатике______________. Исследование численных методов вычисления определенных интегралов
 Скачать 1.28 Mb. Скачать 1.28 Mb.
|
1.4. Метод парабол (Симпсона).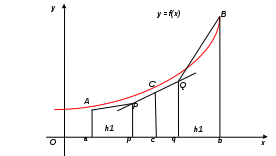 Значительное повышение точности приближенных формул численного интегрирования дает метод парабол (Симпсона). Идея метода исходит из того, что на частичном промежутке дуга некоторой параболы в общем случае теснее прилегает кривой y = f(x), чем хорда, соединяющая концы дуги этой кривой (метод трапеций). Поэтому значения площадей соответствующих элементарных трапеций, ограниченных сверху дугами парабол, являются более близкими к значениям площадей соответствующих частичных криволинейных трапеций, ограниченных сверху дугой кривой y = f(x), чем значения площадей соответствующих прямолинейных трапеций. Значительное повышение точности приближенных формул численного интегрирования дает метод парабол (Симпсона). Идея метода исходит из того, что на частичном промежутке дуга некоторой параболы в общем случае теснее прилегает кривой y = f(x), чем хорда, соединяющая концы дуги этой кривой (метод трапеций). Поэтому значения площадей соответствующих элементарных трапеций, ограниченных сверху дугами парабол, являются более близкими к значениям площадей соответствующих частичных криволинейных трапеций, ограниченных сверху дугой кривой y = f(x), чем значения площадей соответствующих прямолинейных трапеций.Рис. 7. Геометрическая интерпретация метода парабол. Рассмотрим функцию y = f(x). Будем считать, что на отрезке [a; b] она положительна и непрерывна. Найдем площадь криволинейной трапеции aABb (рис. 7). Для этого разделим отрезок [a, b] точкой c = где Откуда получаем Заметим, что aA = f(a), bB = f(b), а pP + qQ = 2f(c) (как средняя линия трапеции), в итоге получаем малую формулу Симпсона 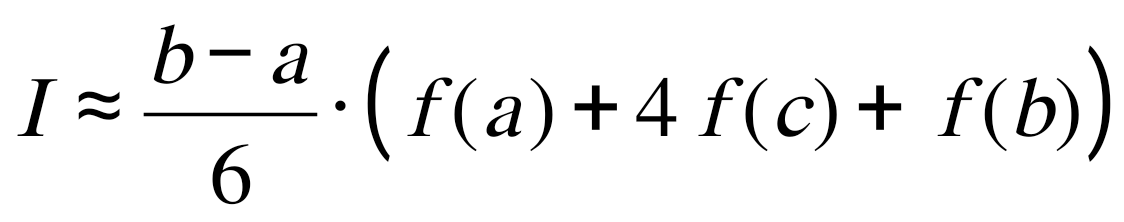 (8) (8)В данном случае дуга ACB заменяется параболой, проходящей через точки A, P, Q, B. Малая формула Симпсона дает интеграл с хорошей точностью, когда график подынтегральной функции мало изогнут, в случаях же, когда дана более сложная функция, малая формула Симпсона непригодна. Тогда, чтобы посчитать интеграл заданной функции нужно разбить отрезок [a, b] на n частей и к каждому из отрезков применить формулу (8). Обязательным требованием, вытекающим из геометрического смысла метода парабол, является то, что n должно быть четным. Пусть Тогда, применяя малую формулу Симпсона к каждой паре получившихся отрезков, имеем 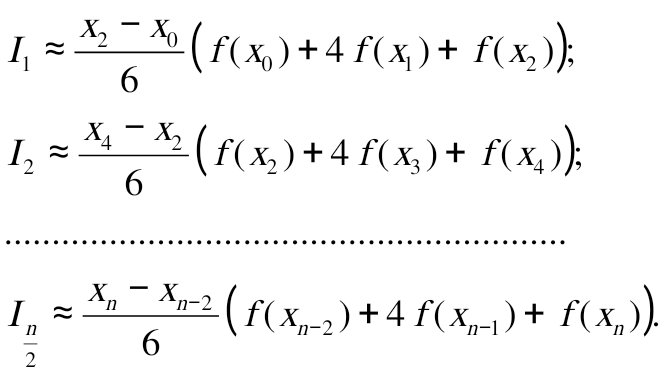 Тогда 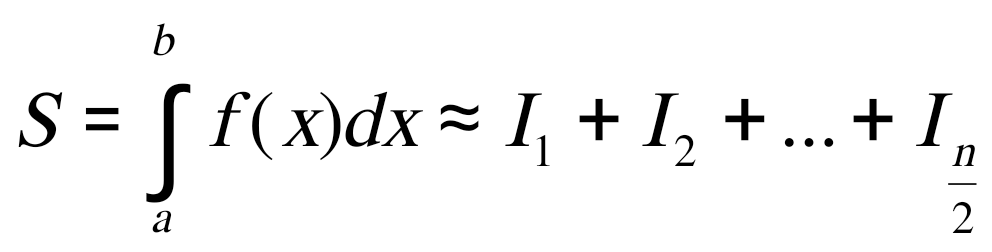 . (9) . (9)Заметим, что во всех выражениях  (10) (10)Сделав замену по формулам (10), вынося общий множитель 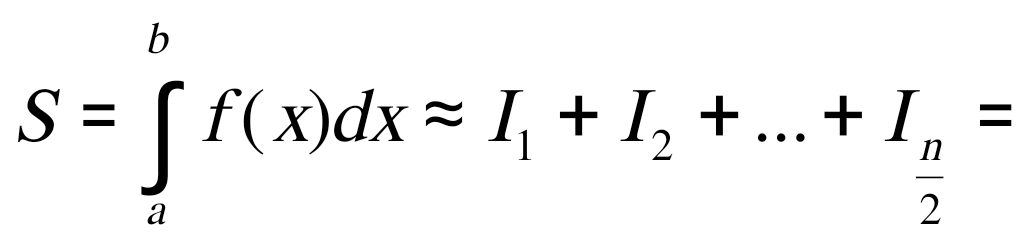 группируем слагаемые Таким образом, получаем «большую» формулу Симпсона, которая имеет вид: 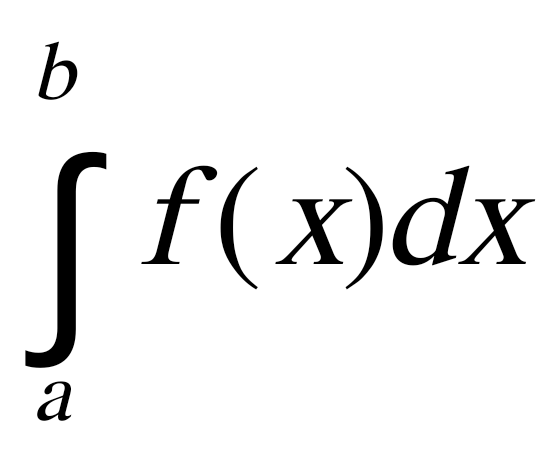 Предлагаем для запоминания следующий вид формулы:  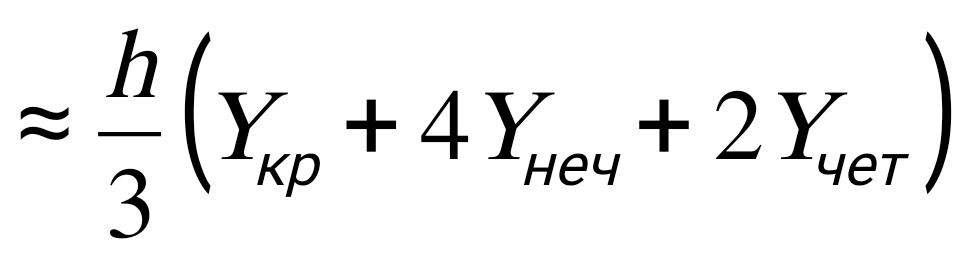 (11’) (11’)где Yкр = y0 + yn, Yнеч = y1 + y3 + … + yn-1, Yчет = y2 + y4 + … + yn-2, а 1.5. Правило Рунге оценки погрешности. В каждой конкретной задаче необходимо определить число точек деления n, необходимое для вычисления интеграла (1) с требуемой точностью ε. Для определения n удобно следующее правило Рунге. Пусть ε – заданная точность вычисления интеграла (1), тогда шаг h должен удовлетворять условию По этому значению h из соотношения Оценку погрешности можно провести также следующим методом Рунге. Пусть Если 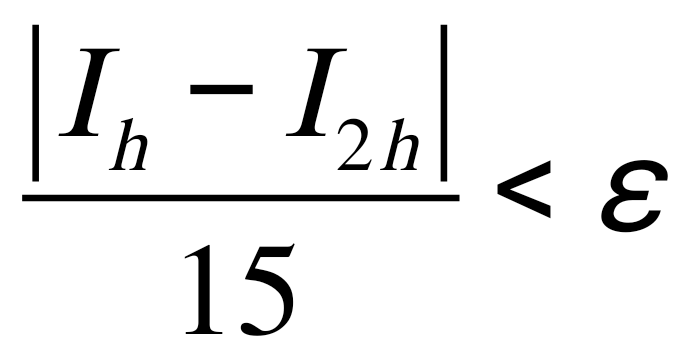 , (13) , (13)где 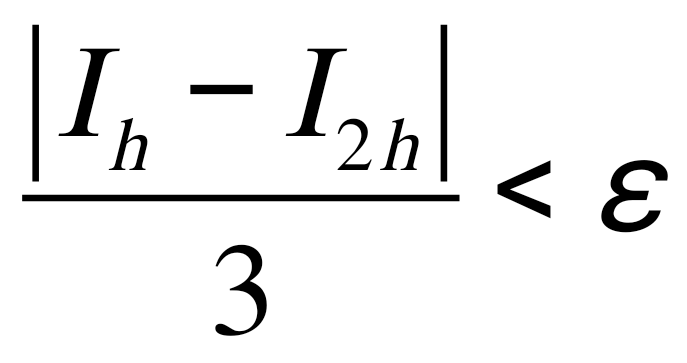 , (14) , (14)где Если неравенство для соответствующего метода не выполняется, то найденное значение интеграла не удовлетворяет заданной точности. Тогда проводят новые вычисления с шагом |
