МС_13_04_2022_вар 5. Решение а Найдём объём выборки 11 13 16 40. Разделив частоты, соответствующие вариантам, на объём выборки, получим

• Название: Решение а Найдём объём выборки 11 13 16 40. Разделив частоты, соответствующие вариантам, на объём выборки, получим
• Дата: 23.04.2022
• Размер: 145.5 Kb.
• Имя файла: МС_13_04_2022_вар 5.doc
• Тип: Решение; #491583

10.5. Выборка задана в виде распределения частот. Найти:

а) распределение относительных частот;

б) эмпирическую функцию распределения;

в) построить график функции F*(x).

xi	10	15	25
ni	11	13	16

Решение. а) Найдём объём выборки

= 11 + 13 + 16 = 40.
Разделив частоты, соответствующие вариантам, на объём выборки, получим:

;

;

.

Тогда распределение относительных частот будет иметь вид:

xi	10	15	20
wi	0,275	0,325	0,4

б) Складывая относительные полученные относительные частоты, найдём эмпирическую функцию распределения:

при x≤ 10 F*(x) = 0;

при 10 < x≤ 15 F*(x) = 0,275;

при 15 < x≤ 20 F*(x) = 0,275 + 0,325 = 0,6;

при x> 20 F*(x) = 0,275 + 0,325 + 0,4 = 1.

Тогда эмпирическая функция распределения будет иметь вид: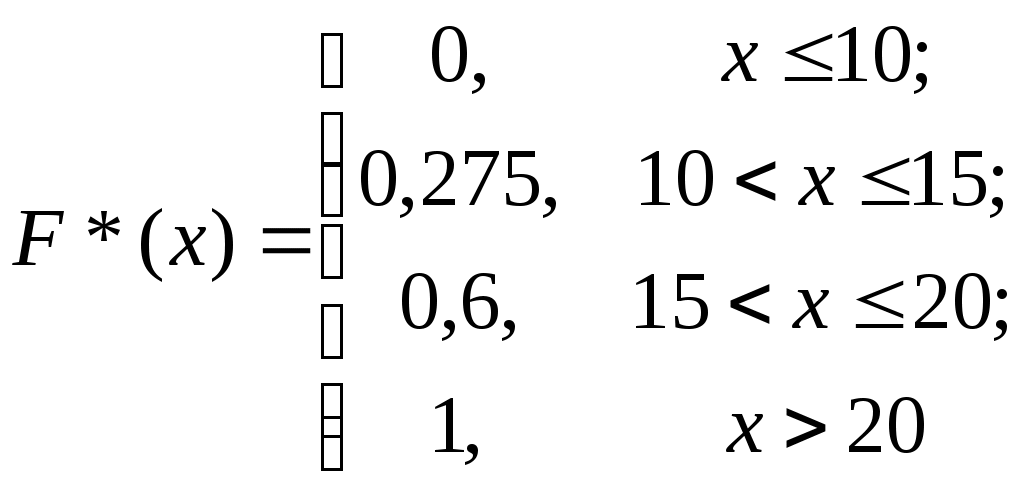


в) построим график функции F*(x):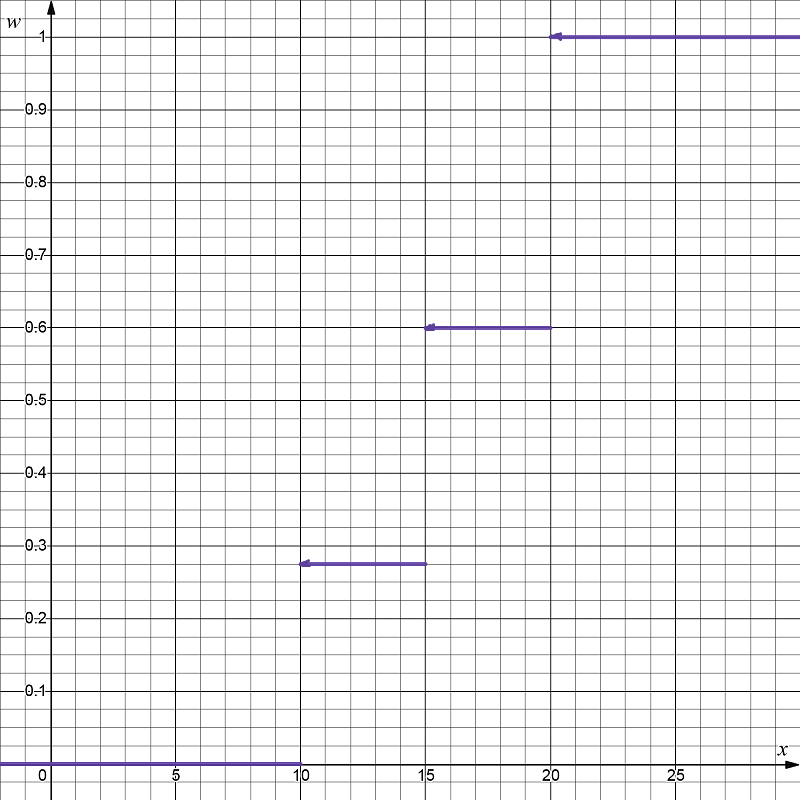



11. 5. Построить полигон частот по данному распределению выборки.

xi	3	5	6	9
wi	10	5	15	20

Решение. Соединив последовательно отрезками точки с координатами (x_i, n_i) получим следующий полигон относительных частот: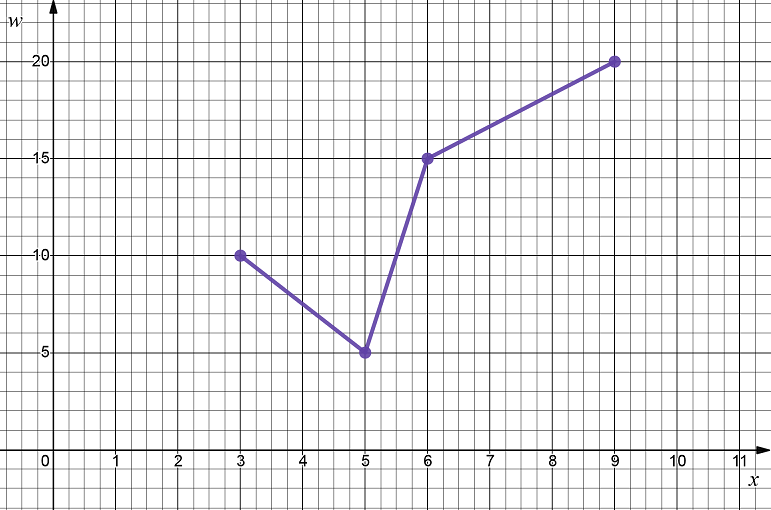



12. 5. Найти выборочную дисперсию по данному распределению выборки объёма n = 30.

xi	354	365	372
ni	?	9	14

Решение. Найдём сначала неизвестную частоту n₁ из условия .

Тогда n₁ + 9 + 14 =30. Отсюда n₁ = 30 – 23 =7.

Тогда получим следующее распределение выборки

xi	354	365	372
ni	7	9	14

Для упрощения вычислений перейдём к условным вариантам

y_i = x_i – 365, для которых распределение выборки будет иметь вид:

xi	–11	0	7
ni	7	9	14

Найдём для них выборочную среднюю о формуле .

Тогда

.

Так как

,

то выборочная дисперсия равна



Так как по свойствам дисперсии эти значения для X и для Y совпадают, то выборочная дисперсия для данного распределения равна
.