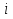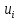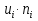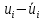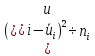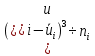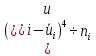Решение а Построим полигон частот. Для этого одну координатную ось возьмем за, например, ось, а другую за. Затем построим точки с координатами, которые соединим отрезками. Полученная ломанная и будет полигоном частот
 Скачать 30.16 Kb. Скачать 30.16 Kb.
|
|
Дано распределение признака 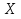
Требуется: а) построить полигон частот; б) найти 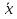 , , 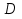 , , 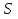 , , 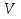 , , 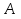 , , 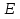 , , 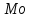 , , 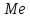 ; ;в) считая, что признак 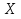 распределен нормально, найти доверительный интервал, покрывающий неизвестное математическое ожидание распределен нормально, найти доверительный интервал, покрывающий неизвестное математическое ожидание 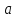 с надежностью с надежностью 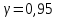 . .Решение а) Построим полигон частот. Для этого одну координатную ось возьмем за 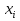 , например, ось , например, ось 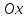 , а другую – за , а другую – за 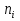 . Затем построим точки с координатами . Затем построим точки с координатами 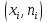 , которые соединим отрезками. Полученная ломанная и будет полигоном частот. , которые соединим отрезками. Полученная ломанная и будет полигоном частот.б) Для того чтобы найти числовые характеристики признака проведем вычисления в таблице Excel с использованием условных вариант.
Так как значения признака равностоящие, то условные варианты находим по формуле: 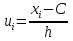 , где , где 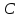 – ложный ноль, – ложный ноль, 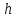 – шаг. – шаг.В качестве ложного нуля возьмем варианту 21, у которой самая большая частота, 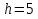 . .Среднее значение признака найдем по формуле: 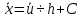 . .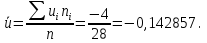 Тогда 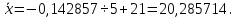 Дисперсию найдем по формуле: 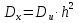 . .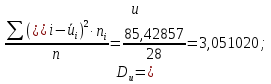 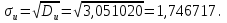 Тогда 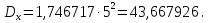 Среднеквадратическое отклонение найдем по формуле: 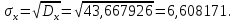 Исправленное среднеквадратическое отклонение равно: 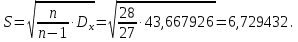 Коэффициент вариации равен: 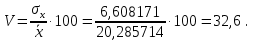 Так как коэффициент вариации меньше 100%, то рассматриваемые значения признака однородные. Коэффициент асимметрии найдем по формуле: 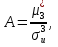 где 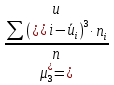 – эмпирический центральный момент третьего порядка. Имеем 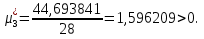 тогда 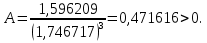 Так как коэффициент асимметрии положительный, правая ветвь статистического распределения длиннее левой относительно среднего. Эксцесс найдем по формуле: 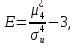 где 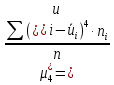 – эмпирический центральный момент четвертого порядка. Имеем 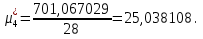 Тогда 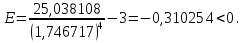 Так как эксцесс отрицательный, то статистическое распределение более сглажено по сравнению с плотностью нормального распределения. Мода – это варианта, у которой самая большая частота. Поэтому 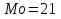 . .Медиана – это варианта, которая делит вариационный ряд пополам. Так как объём распределения равен 28, отсчитывая 14 частот в распределении слева направо и справа налево, получаем, что 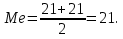 в) Так как признак 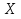 распределен нормально и распределен нормально и 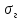 неизвестно, то доверительный интервал, покрывающий неизвестное математическое ожидание неизвестно, то доверительный интервал, покрывающий неизвестное математическое ожидание 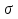 с надежностью с надежностью 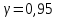 найдём по формуле: найдём по формуле: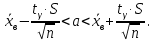 По приложению 3 находим значение 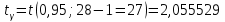 . Так как . Так как 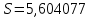 , то имеем , то имеем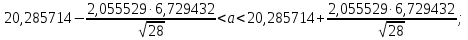 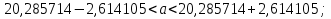 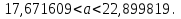 Таким образом, 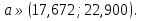 |