Главная страница
Навигация по странице:

  • Задача 5.

  • Решение

  • Задача 6.

    		•

    Задача Построить полигон частот и полигон относительных частот (частостей) 2


    Скачать 78.43 Kb.
    НазваниеЗадача Построить полигон частот и полигон относительных частот (частостей) 2
    Дата26.12.2022
    Размер78.43 Kb.
    Формат файлаdocx
    Имя файлаPRZ 6 (1).docx
    ТипЗадача
    #864875

    ПРЗ №4. Предельные теоремы теории вероятностей и теме Выборочный метод в математической статистике
    Задача 1. Построить полигон частот и полигон относительных частот (частостей):
    2
    7
    8
    15
    16
    17




    15
    35
    64
    55
    21
    10

    Решение:

    Хi
    2
    7
    8
    15
    16
    17


    ni
    15
    35
    64
    55
    21
    10
    200

    wi=ni/n
    0.075
    0.175
    0.32
    0.275
    0.105
    0.05
    1






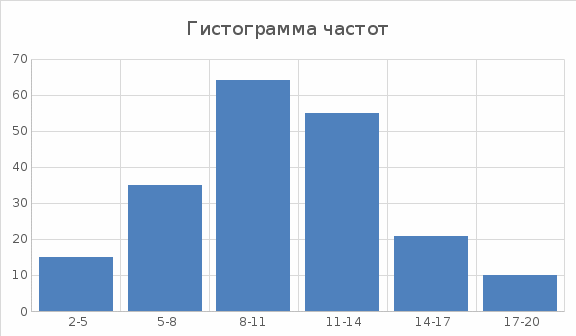
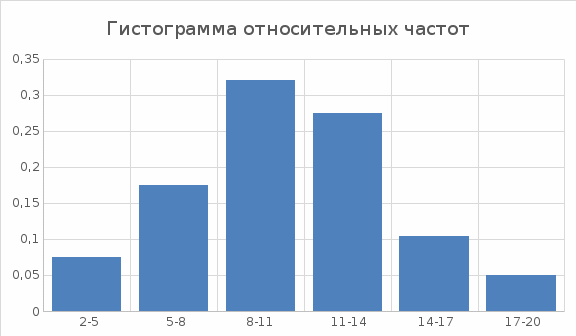
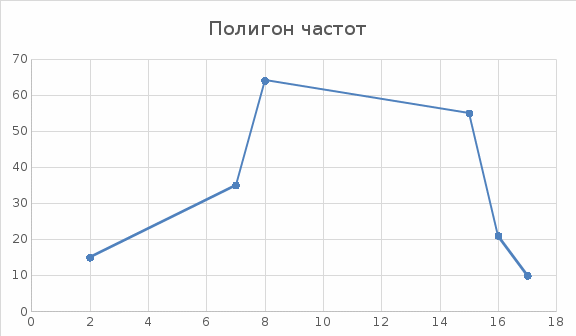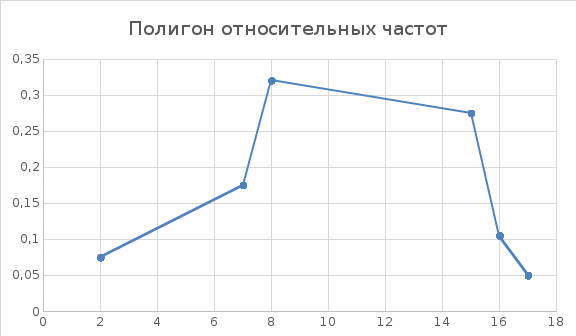    Задача 2. Построить гистограмму частот и относительных частот (частостей)
    2-5
    5-8
    8-11
    11-14
    14-17
    17-20




    15
    35
    64
    55
    21
    10


    Решение:

    Хi
    2-5
    5-8
    8-11
    11-14
    14-17
    17-20


    ni
    15
    35
    64
    55
    21
    10
    200

    wi=ni/n
    0.075
    0.175
    0.32
    0.275
    0.105
    0.05
    1





    Задача 3. Найти несмещенную выборочную дисперсию на основании данного распределения выборки.

    x
    16
    20
    22
    30

    n
    14
    26
    17
    3

    Выборочная дисперсия является смещенной оценкой генеральной дисперсии, поэтому в статистике применяют также исправленную выборочную дисперсию, которая является несмещенной оценкой генеральной дисперсии.

    Решение: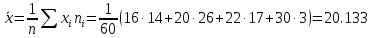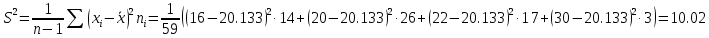




    Задача 4. В городе проживает 250тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей:

    P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности.


    Число детей в семье, xi
    0
    1
    2
    3
    4
    5

    Кол-во детей в семье
    1000
    2000
    1200
    400
    200
    200

    Решение:

    По формуле средней арифметической для интервального вариационного ряда ,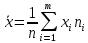

    xi – варианты вариационного ряда, равные срединным значениям интервалов разбиения; ni – соответствующие им частоты; m – число интервалов разбиения, получим: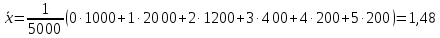



    Аналогично определяется среднее арифметическое квадратов вариант вариационного ряда: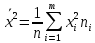

    Получим:

    Следовательно, выборочная дисперсия будет равна: , а среднее квадратическое отклонение: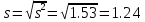

    Границы, в которых с вероятностью 0,954 будет находиться находится среднее число детей в генеральной совокупности, определяются предельной ошибкой выборки, которая возможна с заданной доверительной вероятностью.

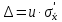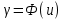    Предельная ошибка бесповторной выборки находится как , где u- аргумент функции Лапласа, соответствующий доверительной вероятности  , т.е. и определяет точность полученных результатов.

    Следовательно, оценка генеральной средней (доверительный интервал) будет удовлетворять следующему двойному неравенству: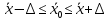

    ,

    где 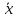– выборочная средняя арифметическая.

    Для заданной доверительной вероятности 0,954 по таблице функции Лапласа находим, что значение ее аргумента будет равно u2.

    Средняя квадратическая ошибка при оценке генеральной средней для собственно-случайной бесповторной выборки достаточно большого объема находим по формуле: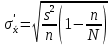

    По условию имеем, что n  5000, N  250000. Подставляя в последнее соотношение числовое значение вычисленной ранее выборочной дисперсии, получим: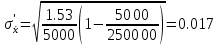

    Следовательно, 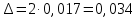, и искомый доверительный интервал для генеральной средней будет иметь вид: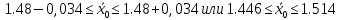



    Задача 5. С целью определения средней фактической продолжительности рабочего дня в гос. учреждении с численностью служащих 480 человек была проведена 25%-ная механическая выборка. По результатам наблюдения оказалось, что у 10% обследованных потери рабочего времени достигали более 45 мин.в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.

    Решение:

    Границы, в которых с вероятностью 0,683 заключена генеральная доля служащих с потерями рабочего времени более 45 мин. в день, определяются предельной ошибкой выборки, которая возможна с заданной доверительной вероятностью.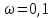



    Средняя квадратическая ошибка собственно-случайной бесповторной выборки при оценке генеральной доли, находится по формуле:



    где 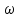– выборочная доля.

    Средняя квадратическая ошибка бесповторной выборки будет равна: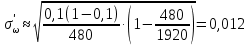



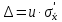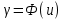    Предельная ошибка бесповторной выборки находится как , где u- аргумент функции Лапласа, соответствующий доверительной вероятности , т.е. и определяет точность полученных результатов.

    Теперь искомый доверительный интервал для генеральной доли определяется соотношением: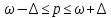

    ,

    Для заданной доверительной вероятности 0,683 по таблице функции Лапласа находим, что значение ее аргумента будет равно u1.

    Следовательно, 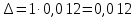, и искомый доверительный интервал для генеральной доли будет иметь вид:


    Задача 6. На предприятии 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что дисперсия доли бесповторной выборки равна 225. с вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.

    Решение:

    Для определения объема повторной выборки, необходимого для того, чтобы гарантировать определенную точность оценки генеральной средней, задаваемую предельной ошибкой выборки , при заданной надежности  , используем формулу: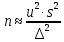



    По условию задачи доверительная вероятность равна  0,954, что соответствует u=2, а предельная ошибка равна =5. Таким образом, объем повторной выборки приблизительно будет равен (округление производим всегда в большую сторону):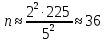



    Зная объем повторной выборки и объем генеральной совокупности, вычисляем объем бесповторной выборки по формуле: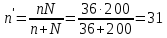


    написать администратору сайта