Теория вероятностей и мат.стат. Решение А) Рассчитаем вероятности появления нужных букв (каждая следующая буква появляется при условии, что предыдущее событие произошло)

• Название: Решение А) Рассчитаем вероятности появления нужных букв (каждая следующая буква появляется при условии, что предыдущее событие произошло)
• Дата: 16.06.2022
• Размер: 20.02 Kb.
• Имя файла: Теория вероятностей и мат.стат.docx
• Тип: Документы; #596565

Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Теория вероятностей и математическая статистика



Группа Сд20М161
Студент
И.Н. Бурков


МОСКВА 2022

Задание 1.

Буквы, составляющие слово РАКЕТА, написаны по од­ной на шести карточках; карточки перемешаны и положены в пакет, а) Чему равна вероятность того, что, вынимая четыре буквы, получим слово РЕКА? б) Какова вероятность сложить слово КАРЕТА при выни­мании всех букв?

Решение:

А) Рассчитаем вероятности появления нужных букв (каждая следующая буква появляется при условии, что предыдущее событие произошло):

Найдем вероятность выбора первой буквы Р:

Количество событий = общему количеству букв = 6.

Из них благоприятных событий (подходящих букв) = 1.

Вероятность по формуле Лапласа:

Р = 1 / 6.

Вероятность, что вторая буква Е:

Р = 1/5 (из оставшихся 5ти букв 1 Е);

Вероятность того, что третья буква будет К:

Р = 1/4 (из оставшихся 4х букв 1 К);

Вероятность того, что четвертая буква будет А:

Р = 2/3 (из оставшихся 3х букв 2 А);

Вероятность взаимосвязанных событий, что поочередно вынуты буквы Р, Е, К, А:

Р = (1 / 6) * (1 / 5) * (1 / 4) * (2 / 3) = 1/180.

Б) 6 карточек: "ААЕКРТ".

Берем первую карту - с вероятностью 1/6 вытащили "К". Осталось 5 карт "ААЕРТ".

Берем вторую - с вероятностью 2/5 вытаскиваем "А". Осталось 4 карты "АЕРТ".

С вероятностью 1/4 вытаскиваем "Р", потом с вероятностью 1/3 – "Е", 1/2 – "Т", 1 – "А".

P("КАРЕТА")=(1/6) * (2/5) * (1/4) * (1/3) * (1/2) * (1)=1/360.

Ответ: а) 1/180 б) 1/360.
Задание 2. Дискретная случайная величина £ задана следующим законом распределения:

£	4	6	10	12
р	0,4	0,1	0,2	0,3

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.

Решение:

£1	4	6	10	12	Суммы
Р1	0,4	0,1	0,2	0,3	1
£1р 1	1,6	0,6	2	3,6	7,8
£21 р1	6,4	3,6	20	43,2	73,2

Математическое ожидание: М(£) = 7,8

Дисперсию вычислим по формуле:

D(£) = M(£²) – (M(£))² = 73,2 – (7,8)² = 73,2 – 60,84 = 12,36

Среднее квадратичное отклонение: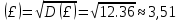

Ответ: М(£) = 7,8,D(£)= 12,36,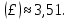


Задание 3.

Возможные значения дискретной случайной величи­ны равны: –2, 1, 4. При условии, что заданы математическое ожидание М(£) = 1,9, а также М(£²) = 7,3, найти вероятности P1*P2*P3,которые соответствуют дискретным значениям случайной величины.

Решение:

Пусть р₁, р₂, р₃– вероятности появления значений x₁,х₂, х₃ соответственно случай­ной величины X. Т.к. случайная величина принимает только 3 значения, то р₁ + р₂+ р₃ =1. По условию р_1:х₁ + р₂х₂ + р₃х₃ = 1,9 иp₁x₁²+p₂x₁²+ р₃х₃² = 7,3.

Получаем систему уравнений: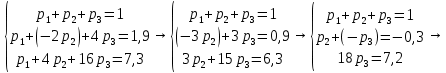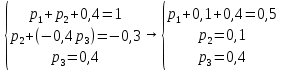





Сделаем проверку. Подставим полученное решение в уравнения из системы и выполним вычисления:

Р₁= 0,5 + 0,1 + 0,4 = 0,5 + 0,1 + 0,4 = 1

Р₂= 0,5 – 2·0,1 + 4·0,4 = 0,5 – 0,2 + 1,6 = 1,9

Р₃ = 0,5 + 4·0,1 + 16·0,4 = 0,5 + 0,4 + 6,4 = 7,3

Ответ: Р₁ = 0,5, Р₂ = 0,1, Р₃ = 0,4.