Виталий Викулин. Решение a Решим систему методом Крамера
 Скачать 40.96 Kb. Скачать 40.96 Kb.
|
|
Задание №1. Решить систему трех линейных уравнений с тремя неизвестными следующими методами: a) методом Крамера; b) методом матричных уравнений; c) методом Жордана-Гаусса. 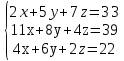 Решение a) Решим систему методом Крамера. 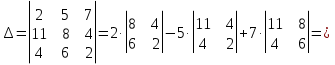 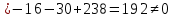 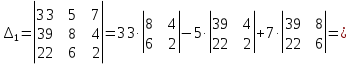 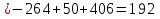 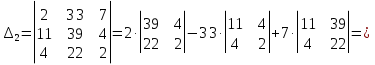 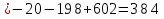 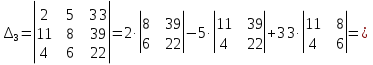 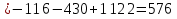 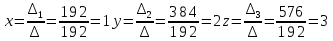 b) Для нахождения решения системы с помощью обратной матрицы запишем систему уравнений в матричной форме 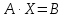 , где , где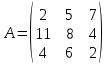 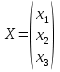 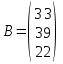 Решение системы в матричной форме имеет вид: 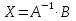 . .Обратную матрицу 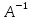 находим по формуле (обратная матрица существует, так как находим по формуле (обратная матрица существует, так как 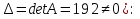 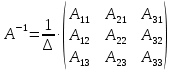 где 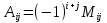 Вычислим алгебраические дополнения всех элементов матрицы 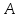 . .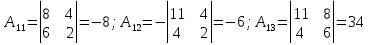 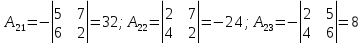 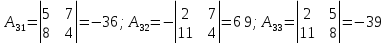 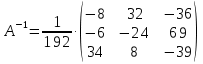 Следовательно, можно найти решение системы уравнений 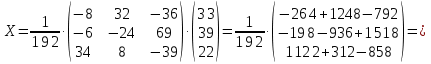 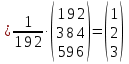 c) Решим систему методом Жордана-Гаусса. Преобразуем расширенную матрицу 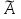 исходной системы исходной системы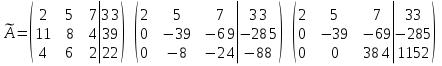 Исходная система эквивалентна системе 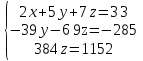 Тогда 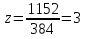 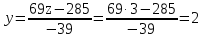 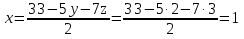 Ответ: 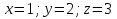 Задание №2. Вычислить пределы числовых последовательностей: 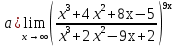 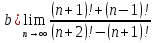 Решение 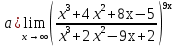 При 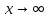 имеем неопределенность вида имеем неопределенность вида 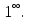 Выражение, стоящее под знаком предела, приводим к такому виду, чтобы можно было воспользоваться вторым замечательным пределом Выражение, стоящее под знаком предела, приводим к такому виду, чтобы можно было воспользоваться вторым замечательным пределом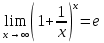 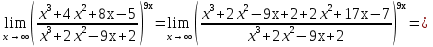 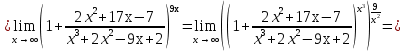 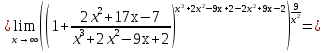 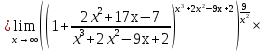 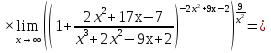 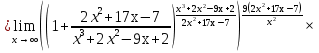 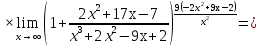 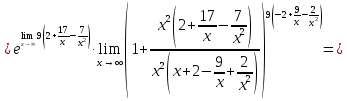 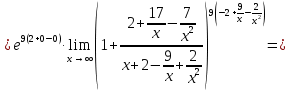 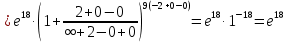 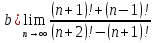 Преобразуем выражение под знаком предела: 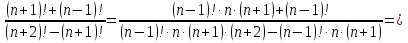 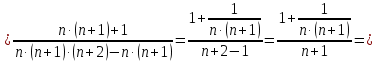 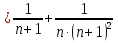 Тогда: 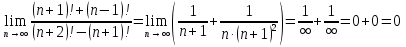 Задание №3. Вычислить производную функции: 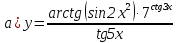 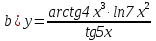 Решение Воспользуемся свойствами 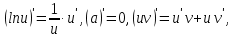 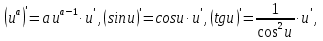 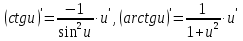 Тогда: 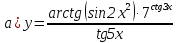 Логарифмируем исходную функцию 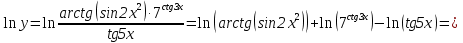 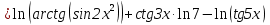 Тогда 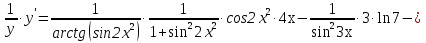 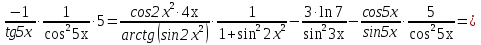 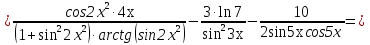 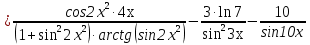 Искомая производная: 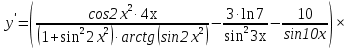 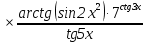 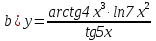 Логарифмируем исходную функцию  Тогда 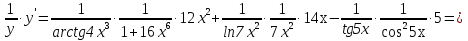 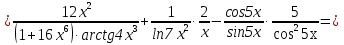 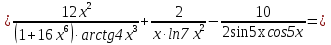 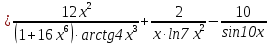 Искомая производная: 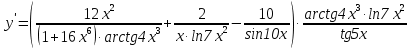 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. –М.: Айрис-пресс, 2003. – 288 с. 2. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 2 / Д.Т. Письменный. –М.: Айрис-пресс: Рольф, 2002. – 256 с. 3. Пискунов, Н.С. Дифференциальное и интегральное исчисление: учебник для втузов. В 2 т. Т. 1 / Н. С. Пискунов.– М.: Интеграл-Пресс, 2001.– 456 с. |
