ргр. РГР. Решение a. Составляем граф марковской цепи

• Название: Решение a. Составляем граф марковской цепи
• Дата: 23.01.2023
• Размер: 133.52 Kb.
• Имя файла: РГР.docx
• Тип: Документы; #901298

Федеральное агентство железнодорожного транспорта

Федеральное государственное бюджетное образовательное учреждение высшего образования

Уральский государственный университет путей сообщения

Кафедра

«Естественнонаучные дисциплины»

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

Марковские процессы

по дисциплине «Теория очередей»

ВАРИАНТ №9

Проверил: Выполнил:

к.физ.-мат.н., доцент студент гр. ИТ-318(з)

Замыслов В.Е. Юрлов А.В.

Екатеринбург

2021

Марковские цепи
Задание №1

Дана матрица переходных вероятностей марковской цепи с дискретным временем.

Требуется:

a. Составить граф марковской цепи.

b. Определить распределения вероятностей системы на первых 8 шагах,

если начальное распределение имеет вид Q(0) = (1,0,0).

c. Определить стационарные вероятности, если они существуют, а в противном случае доказать, что данная цепь не является регулярной.

d. Показать, что предельные вероятности совпадают со стационарными (если цепь регулярна).

Решение:

a. Составляем граф марковской цепи.

На основании матрицы вероятностей переходов P составляем граф.

Матрица P:



Граф: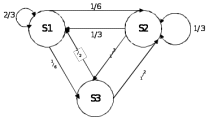


b. Определяем предельное распределение вероятностей системы на основании первых 8 шагов, при начальном распределении Q(0)=(1,0,0).

По рекуррентной формуле находим восьмое распределение и все промежуточные:



















Q₈ - предельное распределение вероятностей.

c. Определяем стационарные вероятности.

Цепь является регулярной, так как из любого существенного состояния можно попасть в любое другое существенное состояние за конечное число шагов. С помощью средств Маткада находим стационарные вероятности.










Проверка:

Умножим получившиеся финальные вероятности на матрицу вероятностей переходов P. В результате должны быть числа, соответствующие финальным вероятностям.






Проверка прошла успешно. Стационарные вероятности найдены правильно.

d. Посмотрим на предельные и стационарные вероятности. По теореме Маркова они должны совпасть, так как данная система регулярна.

Предельные вероятности:



Стационарные вероятност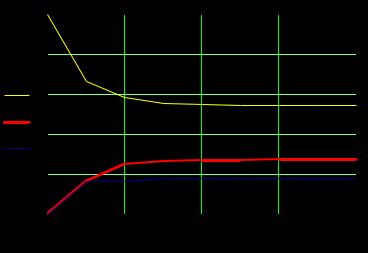и:



Предельные вероятности не совпадают со стационарными, посмотрим на график распределения вероятностей.
Так как данная система является регулярной, то по теореме Маркова предельные и стационарные вероятности должны совпадать. На графике видно, что система за 8 шагов ещё не дошла до стационарных значений, попробуем посмотреть предельное распределение системы на первых 20 шагах.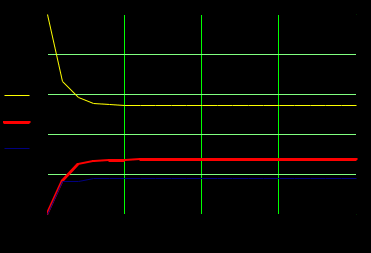


















































Теперь видно, что предельные вероятности примерно равны стационарным. Сравним эти значения до 10 знака после запятой.

Предельные вероятности:






Стационарные вероятности:





Теперь видно, что эти значения совпадают. Эти значения равны, теорема подтвердилась.

Задание №2

Задана матрица ᴧ интенсивностей переходов непрерывной цепи Маркова.

Требуется:

a. Составить размеченный граф состояний системы, соответствующий этой матрице.

b. Записать и решить численным методом систему дифференциальных уравнений Колмогорова самостоятельно выбрав начальное распределение. Построить графики изменения вероятностей состояний и определить (приближенно) предельные вероятности.

c. Найти точные значения стационарных вероятностей состояний и показать, что они совпадают (почему?) с предельными вероятностями.

Решение:

a. На основании матрицы Λ составляем размеченный граф состояний системы.

Матрица Λ:




Размеченный граф состояний системы: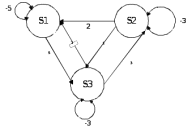


В данном случае цепь регулярна, так как из любого существенного состояния мы можем попасть в другое существенное состояния за конечное число шагов.

Тогда по теореме Маркова предельные вероятности должны быть равны стационарным.

b. С помощью Маткада решаем систему дифференциальных уравнений Колмогорова. Строим графики изменения вероятностей состояний и определяем предельные вероятности.





















Предельные вероятности: (0.231 0.385 0.385)

Г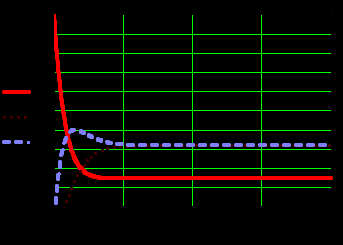
рафики изменения вероятностей


c. Находим точные значения стационарных вероятностей состояний системы.

Чтобы узнать, действительно ли это финальные вероятности, выполним проверку:

В систему дифференциальных уравнений подставляем начальные значения, равные найденным финальным вероятностям.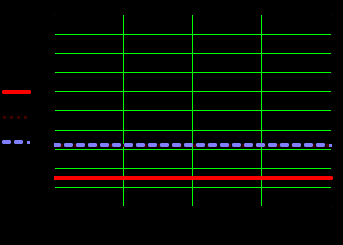





















Так как вероятности на графике с течением времени не изменяются, то финальные вероятности найдены правильно. Чтобы убедиться, что предельные вероятности равны стационарным, посмотрим на них с точностью до десятого знака после запятой.

Предельные вероятности:








Стационарные вероятности:






Теперь видно, что предельные вероятности равны стационарным, теорема подтвердилась.