по дисциплине «Электроника». Решение а Уровень Ферми собственного полупроводника
 Скачать 280 Kb.
|
|
Задача 1 Имеется собственный полупроводник из кремния. а) Докажите, что для потенциала Ферми выполняется соотношение: 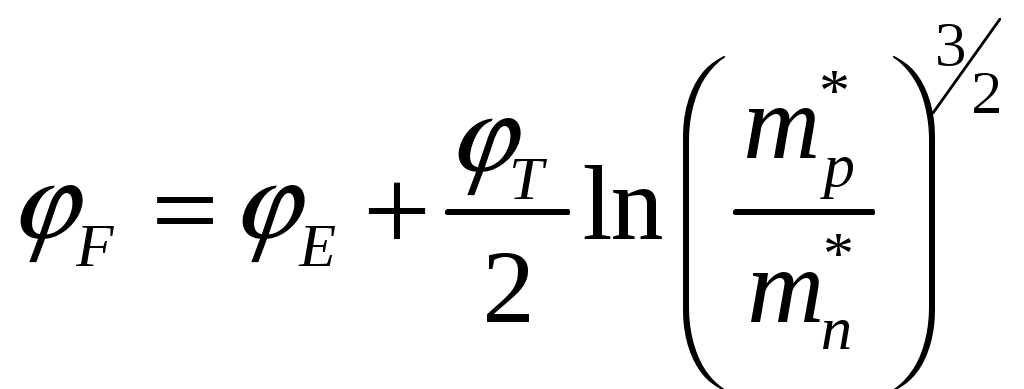 ,где  и  — эффективные массы дырок и электронов соответственно.б) Запишите потенциал Ферми, = .в) Каким должен быть полупроводник (электронный или дырочный), чтобы потенциал Ферми находился точно в середине запрещенной зоны? Вычислите концентрацию легирующего вещества, при котором выполняется это условие. Решение а) Уровень Ферми собственного полупроводника:  ,где  и  – эффективные плотности состояний в валентной зоне и в зоне проводимости соответственно.Эффективные плотности состояний рассчитываются по формулам: 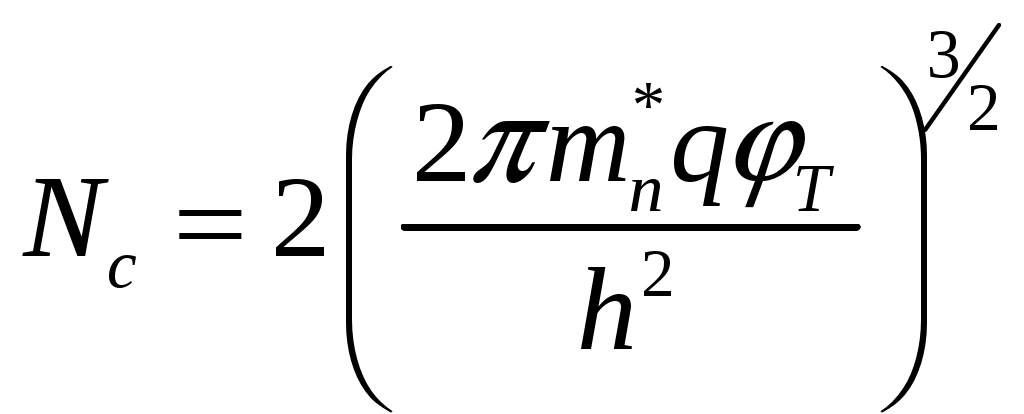 ;  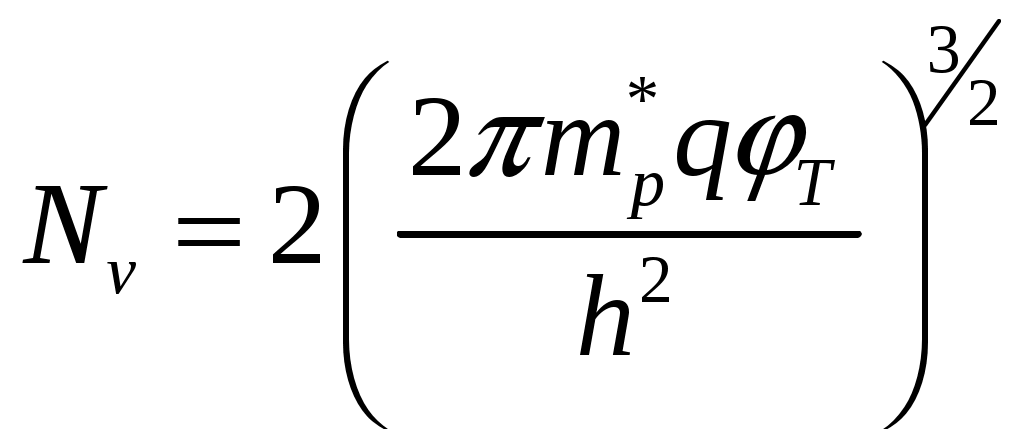.Подставляя в выражение Уровня Ферми получим: 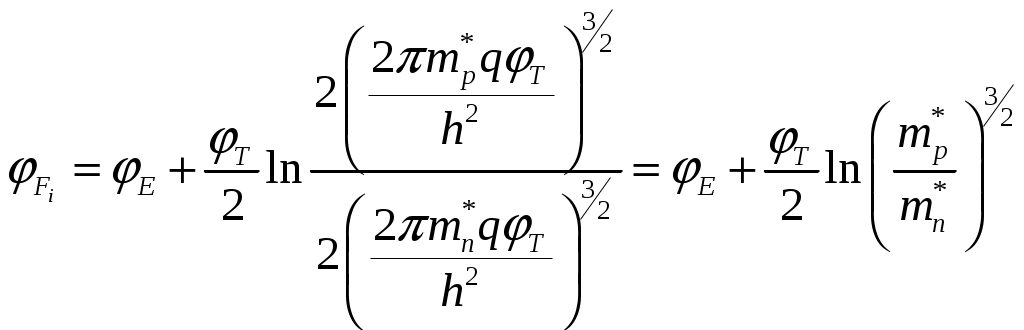 .б) Потенциал Ферми при  равен: В.в) Полупроводник должен быть собственным. Задача 2 Имеется образец германия при 400 К. Вычислите: а) Концентрацию дырок и электронов, если образец легирован атомами сурьмы (элемент пятой группы) с концентрацией 2.4 1013 см-3; б) концентрацию носителей, которая установится после того, как проведено легирование атомами индия (элемент третьей группы) с концентрацией 4.8 1013 см-3. Решение а) У сурьмы валентность 5, соответственно, по отношению к германию он выступает донором. Полупроводник электронный (типа n) [3]. Неосновными носителями являются дырки. Так как заданная температура высока, определим критическую температуру германия [4]:  К,где для германия  ;  ;  Ом·м.Таким образом, так как заданная температура превышает критическую, то концентрация электронов в области высоких температур ( 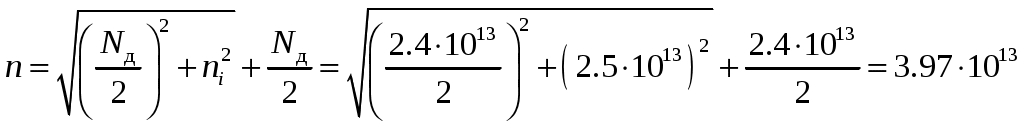 ): см3,где  см3 – концентрация атомов сурьмы; см3 – концентрация собственных носителей заряда.Концентрация дырок в области высоких температур ( 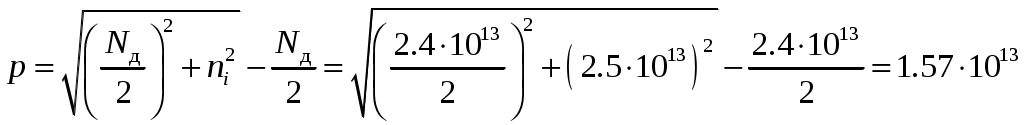): см3.б) У индия валентность 3, соответственно, по отношению к германию он выступает акцептором. Полупроводник дырочный (типа p) [4]. Неосновными носителями являются электроны. Таким образом, так как заданная температура превышает критическую, то концентрация дырок в области высоких температур ( 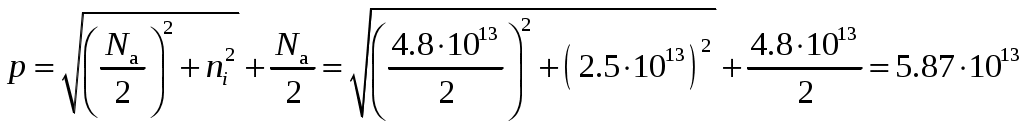): см3,где  см3 – концентрация атомов сурьмы; см3 – концентрация собственных носителей заряда.Концентрация электронов в области высоких температур ( 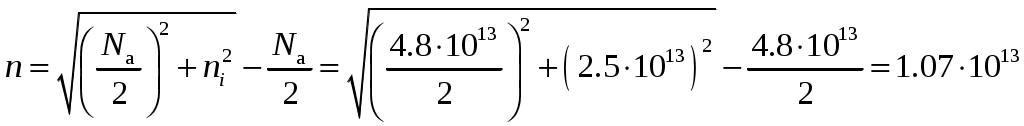): см3.Задача 3 Переход образован полупроводниками из германия. а) Докажите, что высота потенциального барьера равна:  ,  ,где  — исходные концентрации основных носителей в полупроводниках p- и n-типов и собственные концентрации соответственно.Чему будет равен потенциальный барьер, если оба полупроводника собственные? б) Рассчитайте величину диффузионного потенциала при  0С,  и  .Решение а) Для доказательства используем формулы (1.16) и (2.4а) из [4]:  ; (1.1) . (1.2)Из формулы (1.1) выразим:  .Подставив в (1.2), получим: 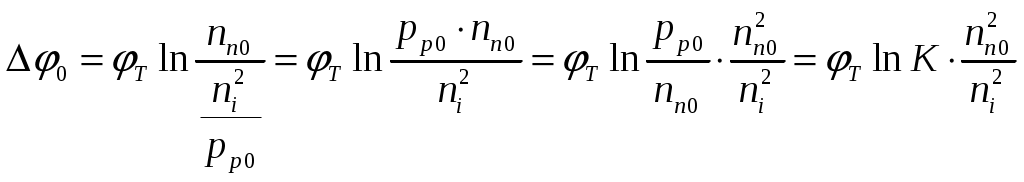 ,б) Рассчитаем величину диффузионного потенциала при °С, если . Расчёт произведём с использованием пакета MathCAD v. 11, ниже приведён листинг расчёта с исходными данными и результатами.При расчётах примем, что построения проводились для температуры 300 ºС, или 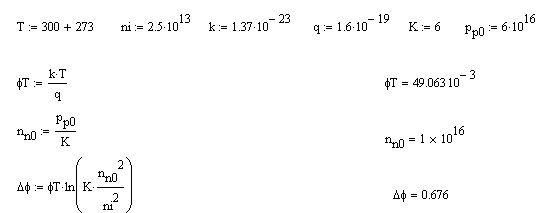 К. Тогда температурный потенциал формула (1.3) из [4]: мВ,где  Дж/ºС – постоянная Больцмана (таблица 1.2 из [4]); Кл – элементарный заряд (таблица 1.2 из [14]). Задача 4 Постройте энергетические диаграммы для перехода, образованного полупроводниками из германия, приняв за нулевой потенциал «дна» зоны проводимости дырочного полупроводника. Диаграммы постройте для трёх значений напряжений внешнего источника:  ;  ;  .Потенциалы Ферми в дырочном и электронном полупроводнике определяются формулами:  ;  .Замечание. Необходимо построить зонные диаграммы, а не высоту потенциального барьера. Решение Энергетические диаграммы представлены на рисунке 1. 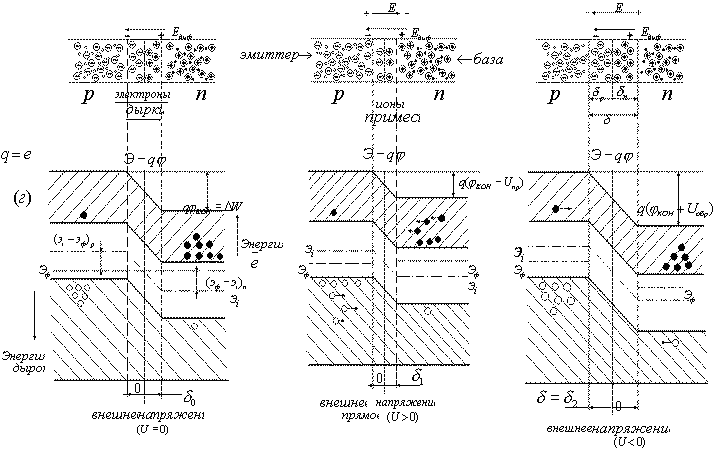 Рисунок 1 1. При одних и тех же концентрациях примесей высота потенциального барьера больше в p - n - переходах, созданных в полупроводниках с большей шириной запрещённой зоны. 2. Высота потенциального барьера возрастает при увеличении концентрации примесей в соответствующих областях. 3. с увеличением температуры высота потенциального барьера уменьшается. Например: при  ,  ,  К для p - n - перехода на основе Ge  В; для перехода на основе кремния  В.  эВ (при К),  эВ (при К).Для большинства: Ge p - n – переходов  В.Si p - n - переходов  В.Задача 5 Имеются диоды, выполненные из германиевых и кремниевых полупроводников. а) Докажите справедливость выражения: 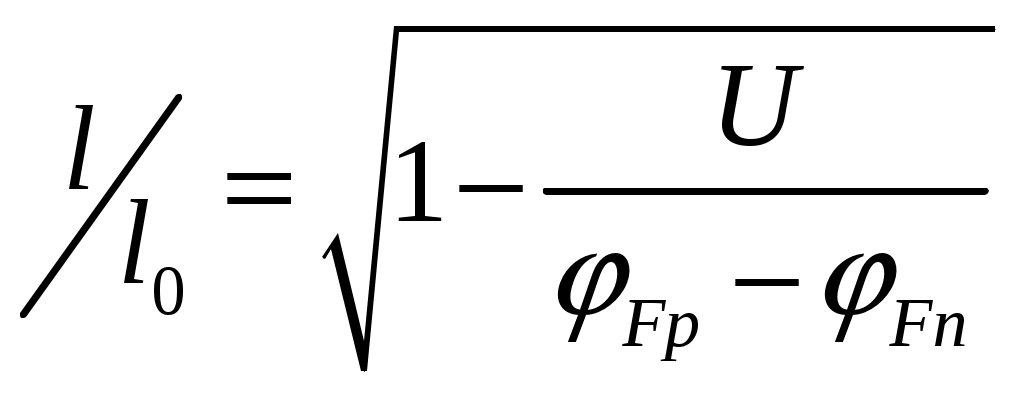 ,где  — ширина перехода; — ширина перехода в равновесном состоянии; — уровни Ферми в примесных полупроводниках до образования перехода.б) Постройте график относительного изменения ширины перехода в диодах при изменении напряжения (обратное смещение):  . Сделайте выводы.Решение а) Ширина перехода в равновесном состоянии определяется формулой (2.9б) из [2]: 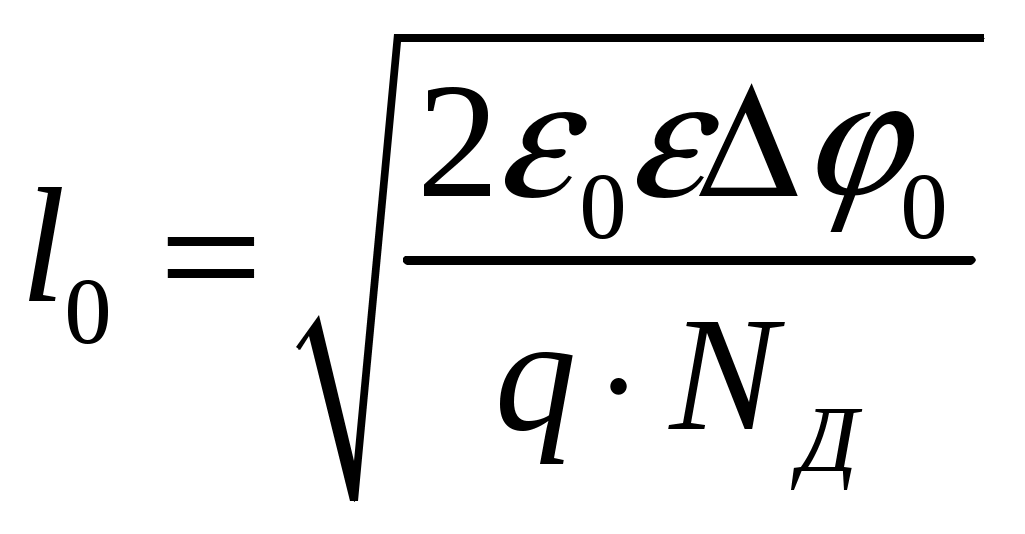 .Ширина перехода в неравновесном состоянии определяется формулой (2.11) из [2]: 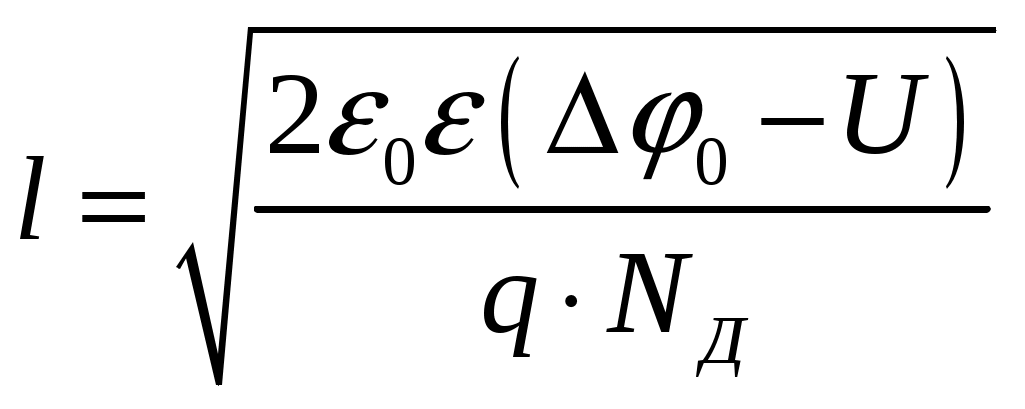 .Поделив эти выражения, получим: 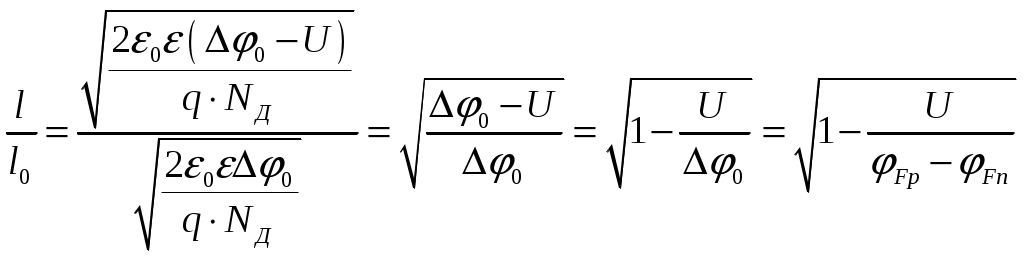 .б) Построим график относительного изменения ширины перехода в диодах при изменении напряжения (обратное смещение)  .Расчёт произведём с использованием пакета MathCAD v. 11, ниже приведён листинг расчёта с исходными данными и результатами. Для германиевого диода: 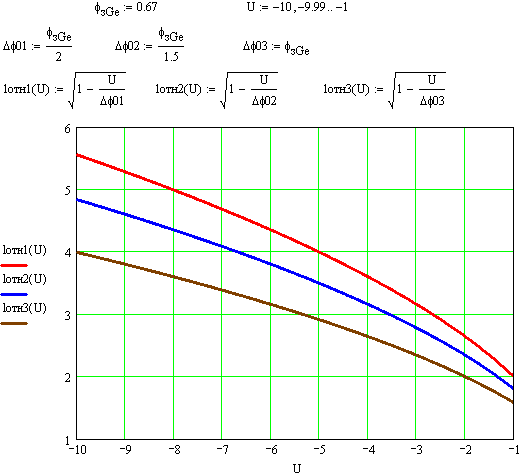 Для кремниевого диода: 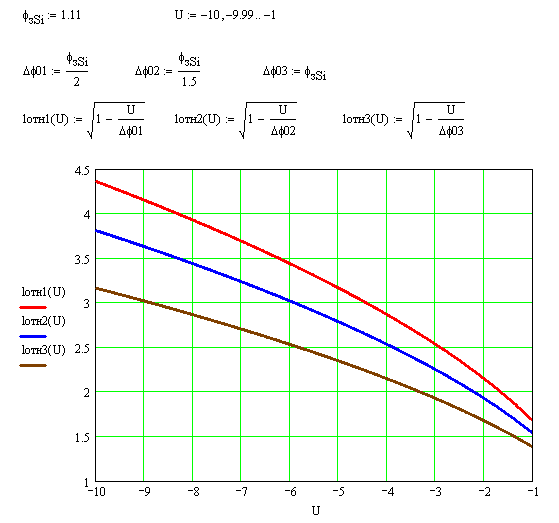 Анализируя результаты, видно, что для германиевого диода относительная ширина перехода выше чем у кремниевого. Также видно, что с увеличением высоты барьера, относительная ширина перехода уменьшается. Список используемой литературы 1. Ицкович В.М. Электроника : учебное методическое пособие / В. М. Ицкович ; под ред. В. А. Шалимова. – Томск : ФДО, ТУСУР, 2017. – 76 с. 2. Ицкович В.М. Электроника и микроэлектроника: Учебное пособие. - Томск: Томский межвузовский центр дистанционного образования, 2000. - 246 с. 3. Ицкович В.М. Электроника: Учебное пособие. В 2-х разделах. — Томск: Томский межвузовский центр дистанционного образования, 2005. — Р.1. — 209 с. 4. Ицкович В.М. Электроника: Учебное пособие. В 2-х разделах. — Томск: Томский межвузовский центр дистанционного образования, 2005. — Р.2 — 120 с. 5. Степаненко И. П. Основы теории транзисторов и транзисторных схем. Изд. 4-е, перераб. И доп. М., «Энергия», 1977. 672 с. |