Главная страница
Навигация по странице:

  • Ответ

  • Задание №5 Имеется 6 задержанных. Для проведения расследования необходимо устроить парные очные встречи каждого с каждым. Сколько таких встреч нужно организовать Решение

  • Решение

  • Список литературы

    		•

    Решение а в 1


    Скачать 188.5 Kb.
    НазваниеРешение а в 1
    Дата24.05.2021
    Размер188.5 Kb.
    Формат файлаdoc
    Имя файла63Д.doc
    ТипРешение
    #209170

    ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ

    Вариант - 3

    Задание №1


    Построить таблицу истинности логических формул

    .

    Решение:

    А
    В










    1
    1
    1
    0
    1
    1
    1

    1
    0
    0
    1
    1
    0
    1

    0
    1
    0
    1
    1
    1
    1

    0
    0
    0
    1
    1
    0
    0


    .

    Решение:

    А
    В
    С










    1
    1
    1
    1
    0
    0
    0
    1

    1
    1
    0
    1
    0
    0
    0
    1

    1
    0
    1
    0
    1
    1
    1
    1

    1
    0
    0
    0
    1
    1
    1
    1

    0
    1
    1
    0
    1
    1
    1
    1

    0
    1
    0
    0
    1
    1
    1
    1

    0
    0
    1
    0
    1
    1
    1
    1

    0
    0
    0
    0
    1
    1
    1
    1


    Формула является тождественно-истинной.
    Задание №2
    Проверить правильность суждений средствами логики суждений: «Если бы он не пошел в кино, то он не получил бы двойки. Если бы он подготовил домашнее задание, то не пошел бы в кино. Он получил двойку. Значит, он не подготовил домашнее задание».

    Решение:

    А – пошёл в кино,

    В – получил двойку,

    С – подготовил домашнее задание.

    Суждение можно записать с помощью формулы: .

    А
    В
    С














    F

    1
    1
    1
    0
    0
    0
    1
    0
    0
    0
    1

    1
    1
    0
    0
    0
    1
    1
    1
    1
    1
    1

    1
    0
    1
    0
    1
    0
    1
    0
    0
    0
    1

    1
    0
    0
    0
    1
    1
    1
    1
    1
    0
    1

    0
    1
    1
    1
    0
    0
    0
    1
    0
    0
    1

    0
    1
    0
    1
    0
    1
    0
    1
    0
    0
    1

    0
    0
    1
    1
    1
    0
    1
    1
    1
    0
    1

    0
    0
    0
    1
    1
    1
    1
    1
    1
    0
    1


    Видим, что формула тождественна истинна.

    Суждение правильное.


    Задание № 3

    Решить системы линейных уравнений матричным методом и методом Гаусса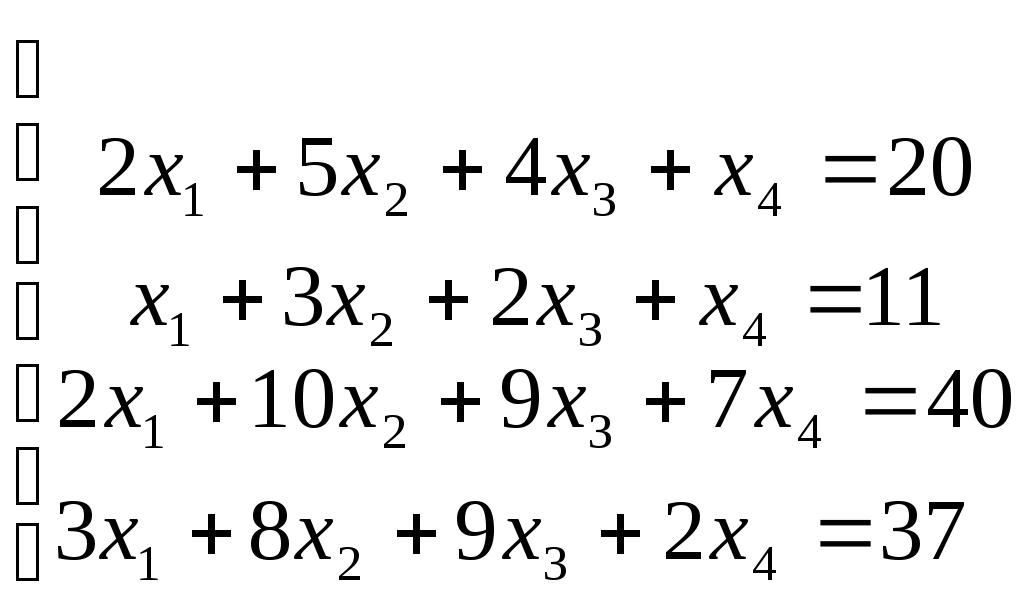



    Решение:

    1) методом Гаусса;

    Произведем элементарные преобразования над строчками расширенной матрицы системы: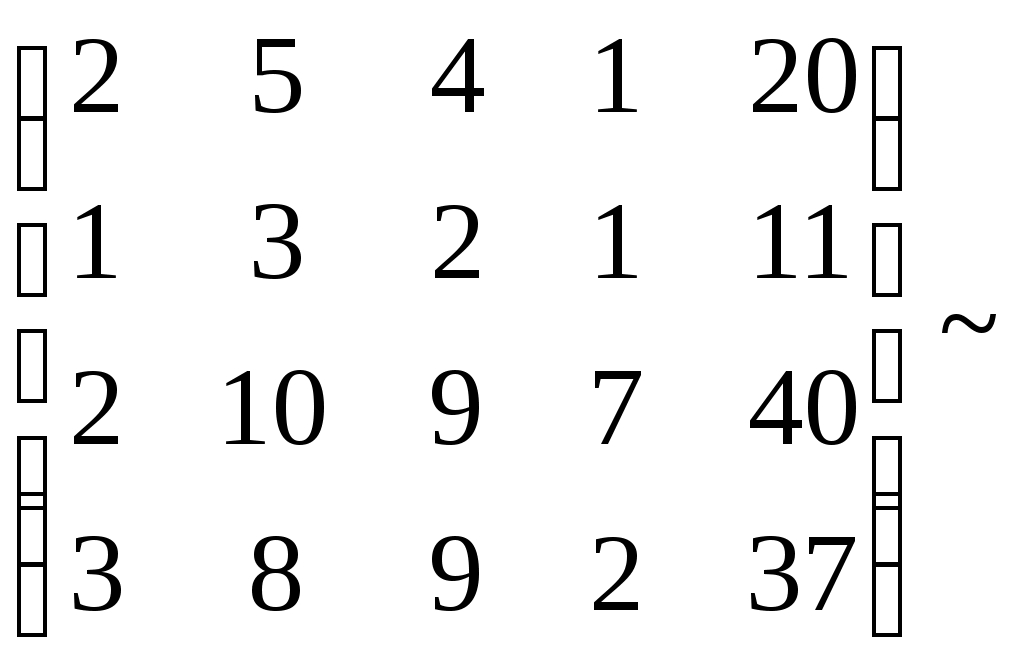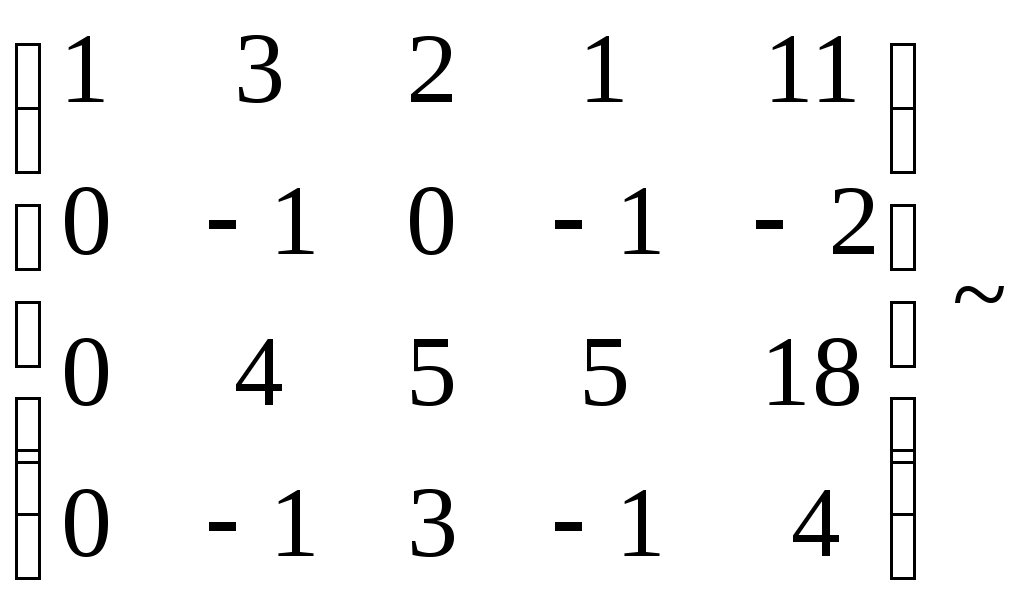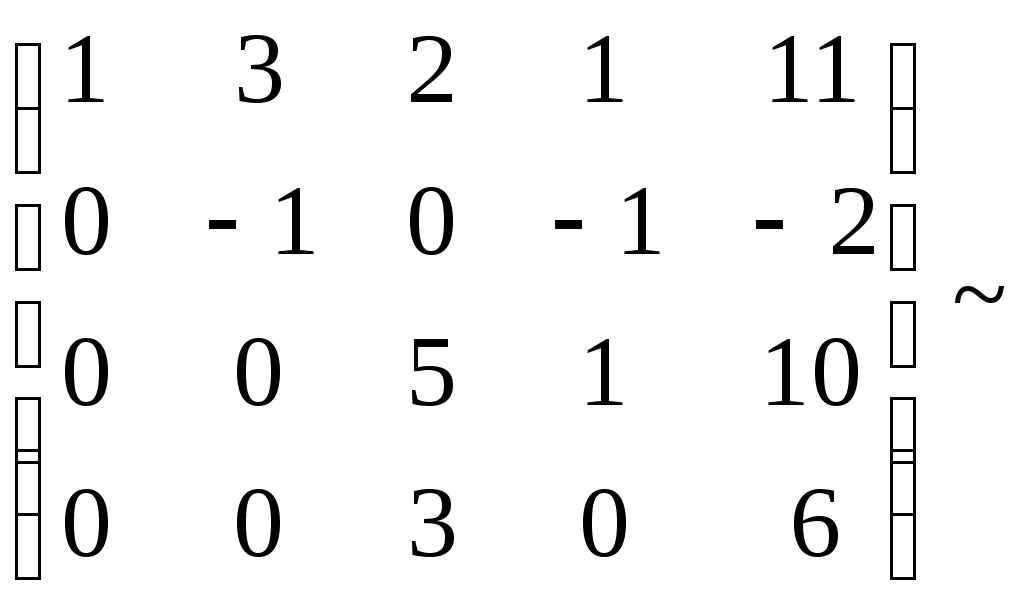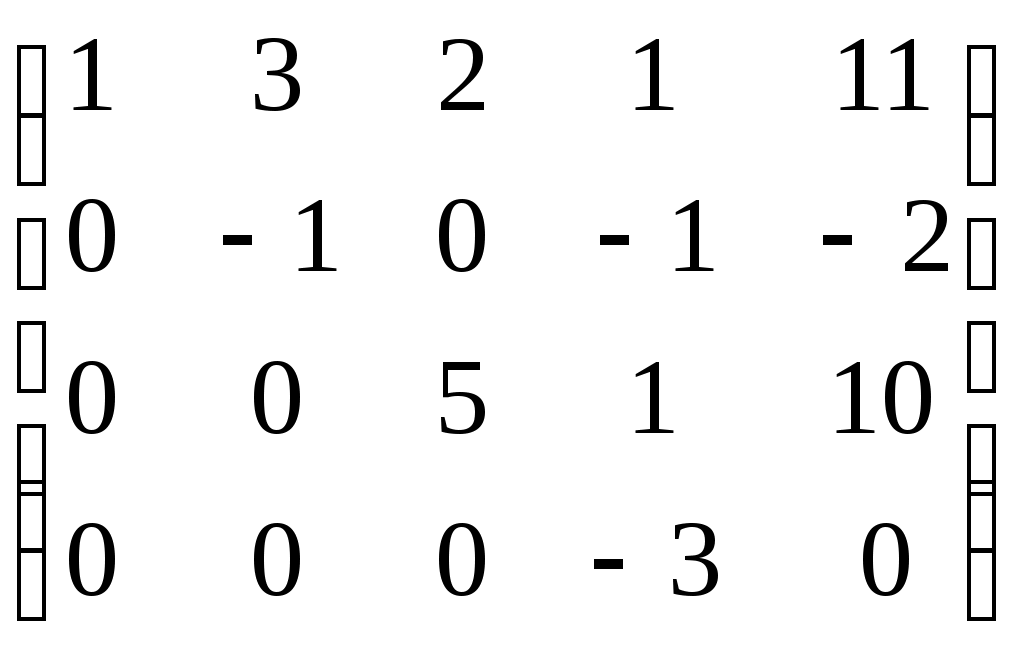

    .

    Полученная матрица соответствует системе: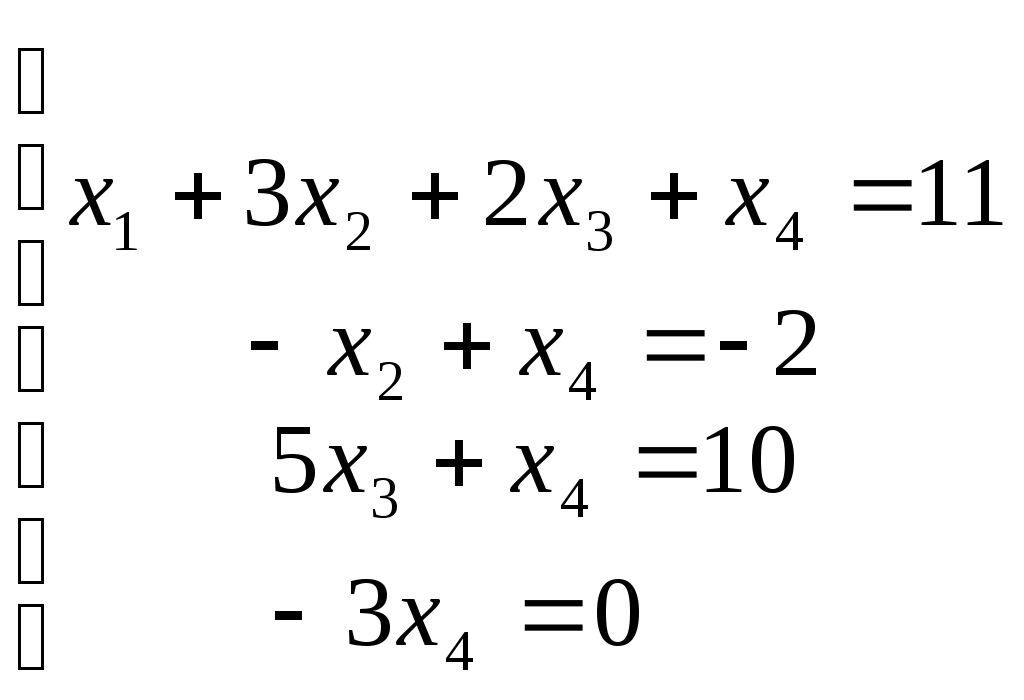



    осуществляя обратный ход, находим:

    .

    ;

    ;

    .

    .
    в) с помощью обратной матрицы:

    Более удобной формой записи системы линейных уравнений является матричная форма

    A·X = B.

    Система уравнений имеет однозначное решение, если матрица А невырожденная, т.е. если определитель матрицы А D¹ 0. Решение уравнений в матричной форме задается как X = A-1B.

    В нашем случае: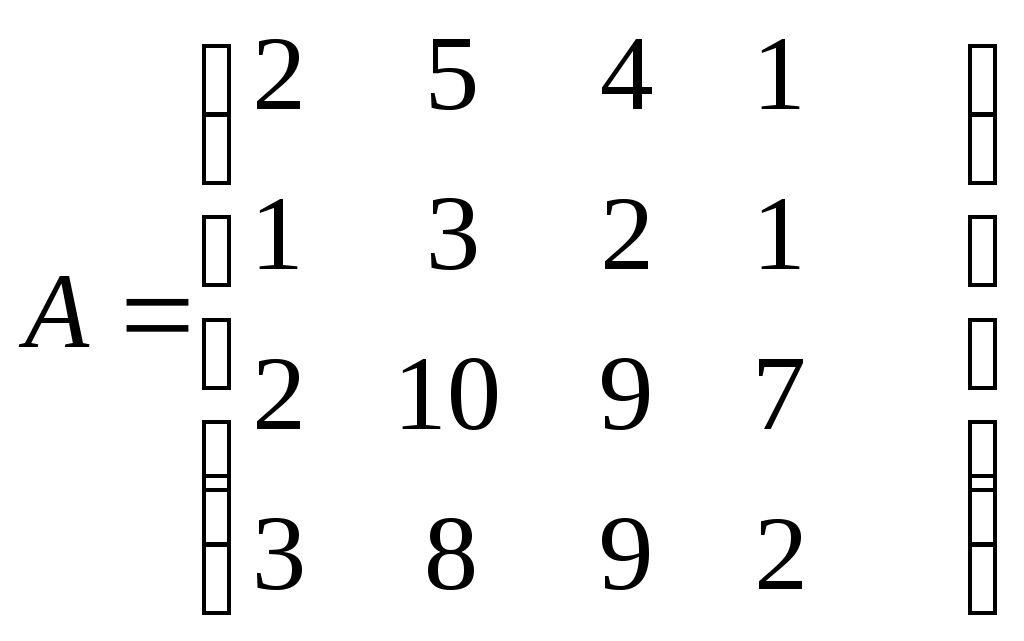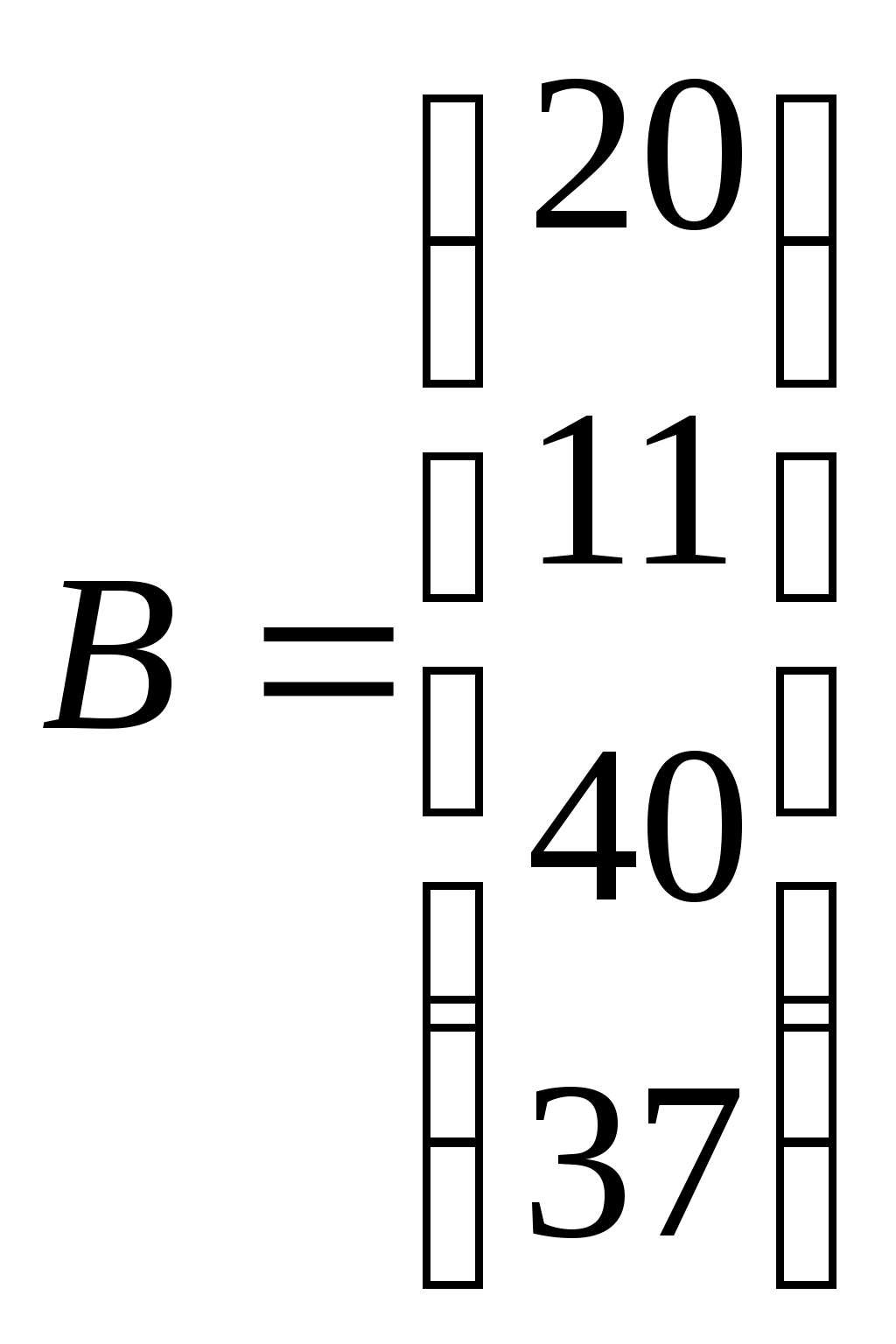

    , .

    Вычислим обратную матрицу: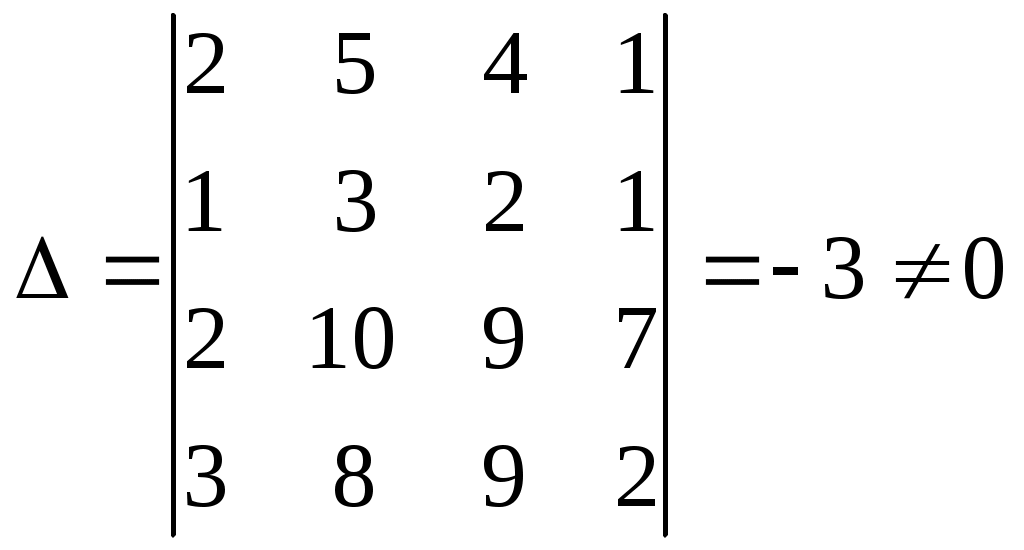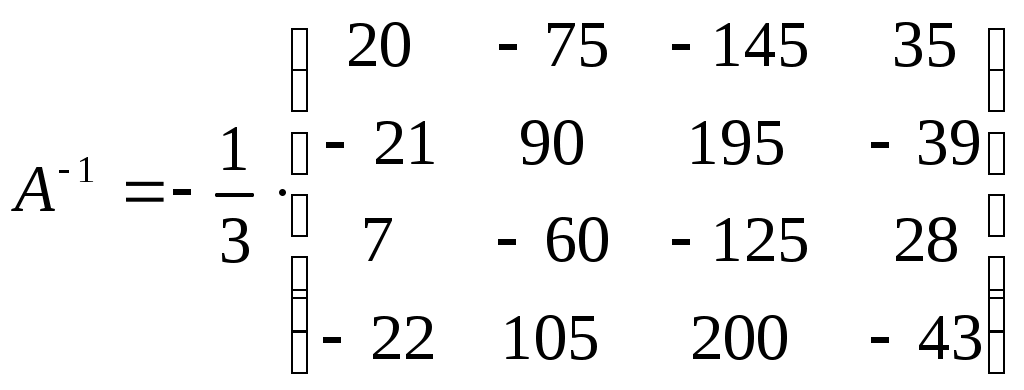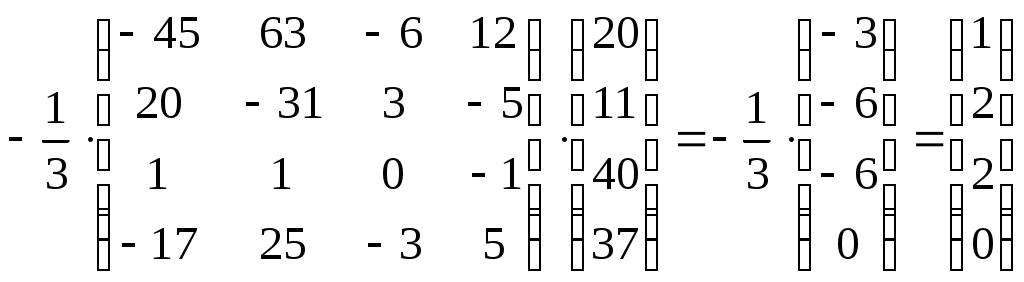

    .

    .

    .

    Ответ: .
    Задание №4
    В юридической фирме 22 юристов является специалистом по гражданскому праву, 25 – по уголовному, 24 – по административному. Кроме того, 5 сотрудника являются специалистами по гражданскому и уголовному, 7 – по уголовному и административному, 5 – по гражданскому и административному, а 5 сотрудников являются специалистами во всех трех правах. Сколько сотрудников работает в фирме?

    Решение:

    Пусть |А|, |В|, |С| – число юристов, являющихся соответственно специалистами по гражданскому, уголовному и административному праву.

    По условию |А| =22 , |В|=25 , |С|=24, ; ; ; .

    .

    .

    Решение задачи легко иллюстрируется на диаграмме Венна: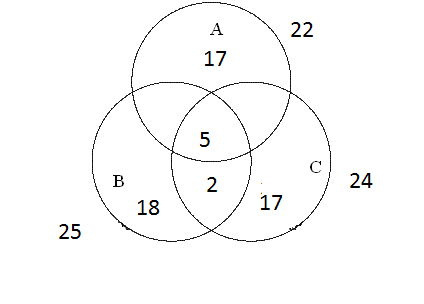



    Всего 59 сотрудников работает в фирме.

    Задание №5
    Имеется 6 задержанных. Для проведения расследования необходимо устроить парные очные встречи каждого с каждым. Сколько таких встреч нужно организовать?

    Решение:

    Каждая очная встреча между двумя задержанными из 6 отличается от других только составом пар участников, т.е. представляет собой сочетание из 6 элементов по 2:

    Ответ: 15 таких встреч нужно организовать.
    Задание №6
    В бригаде ОМОН число сотрудников 6. Для выполнения задания их них нужно отобрать группу из 9 человек. Сколько таких групп можно создать?

    Решение:

    Из 6 человек группу из 9 человек составить невозможно.

    Ответ: 0 групп.
    Задание №7

    Дана выборка количества приводов в милицию в течении года для 20 детей из неблагополучных семей. Составить статистический ряд по данным выборки. Построить полигон, гистограмму и кумуляту.

    2
    1
    5
    5
    0
    2
    3
    2
    2
    1
    3
    2
    2
    4
    2
    0
    1
    2
    0
    3

    Решение:

    Составим статистический ряд по данным выборки:
    0
    1
    2
    3
    4
    5




    3
    3
    8
    3
    1
    2
    20



    3
    6
    14
    17
    18
    20




    Построим полигон: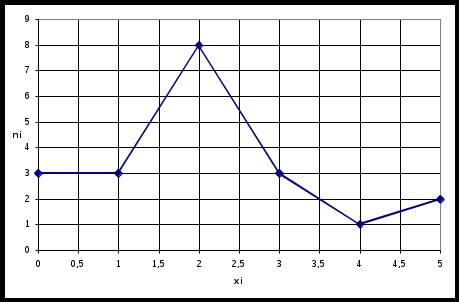



    Построим гистограмму: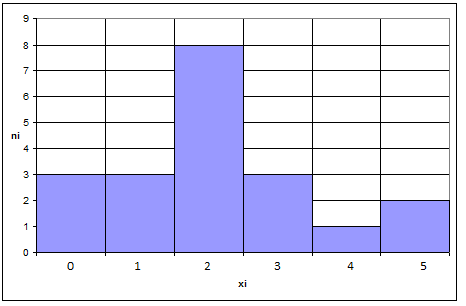



    Построим кумуляту: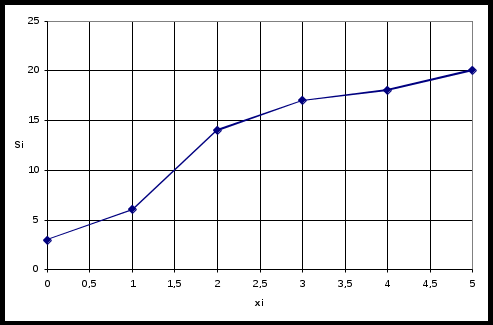


    Список литературы

    1. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике /В. Е. Гмурман. - М., Высш.шк., 2004.- 404 с.

    2. Гмурман, Владимир Ефимович. Теория вероятностей и математическая статистика:учебное пособие для вузов /В. Е. Гмурман.-Изд. 12-е, перераб.-М.:Высшая школа,2009.-478с.

    3. Коробейникова, И.Ю. Теория вероятностей. Случайные величины : Учеб. пособие / И. Ю. Коробейникова, Г. А. Трубецкая. - Челябинск : АТОКСО, 2004. - 86 с

    4. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов / Н.Ш. Кремер.— М.: ЮНИТИ-ДАНА, 2004. - 573 с.

    5. Лихтарников, Л.М. Математическая логика : курс лекций : задачник-практикум и решения : учеб. пособие / Л. М. Лихтарников, Т. Г. Сукачева. - 3-е изд., испр. - СПб. ; М. ; Краснодар : Лань, 2008. - 276 с.

    6. Мальцев, А.И. Основы линейной алгебры : учебник / А. И. Мальцев. - 5-е изд., стер. - СПб. ; М. ; Краснодар : Лань, 2009. - 470 с.

    7. Математика для юридических специальностей : учеб. пособие для студ. вузов / ред. С. Я. Казанцев. - М. : Академия, 2012. - 217 с. - (Университетский учебник. Высшая математика и ее приложения к юриспруденции). - Библиогр.: С. 174-176

    8. Письменный Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам / Д.Т. Письменный. - 3-е изд. - М.: Айрис-пресс, 2008. -288 с.

    написать администратору сайта