Высшая математика 3 вариант. КР матем - 1 курс. Задача Решить систему уравнений методом Крамера, методом Гаусса, матричным методом

• Название: Задача Решить систему уравнений методом Крамера, методом Гаусса, матричным методом
• Анкор: Высшая математика 3 вариант
• Дата: 01.12.2022
• Размер: 1.45 Mb.
• Имя файла: КР матем - 1 курс.docx
• Тип: Задача; #823190
• страница: 1 из 4

Задача 1. Решить систему уравнений : методом Крамера, методом Гаусса, матричным методом: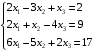



Метод Крамера:

Запишем формулы Крамера:
x₁ = det A₁ / det A

x₂ = det A₂ / det A

x₃ = det A₃ / det A
На ноль делить нельзя. Поэтому если det A равен нулю, то использовать формулы Крамера невозможно.
Вычислим det A.   

det A =		2	-3	1		=
		2	1	-4
		6	-5	2

К элементам строки 3 прибавляем соответствующие элементы строки 1, умноженные на -2.   

=		2	-3	1		=
		2	1	-4
		2	1	0

К элементам столбца 1 прибавляем соответствующие элементы столбца 2, умноженные на -2.   

=		8	-3	1		=
		0	1	-4
		0	1	0

Разложим определитель по элементам строки 3.  

= ( -1) 3 + 2 * 1 *										8		1			=
										0		-4
= -		8	1		=
		0	-4

= - ( 8 * ( -4) - 1 * 0 ) =

= - ( -32 + 0 ) =

= 32
det A не равен нулю. Использование формул Крамера возможно.

Вычислим det A₁   

det A1 =		2	-3	1		=
		9	1	-4
		17	-5	2

К элементам столбца 1 прибавляем соответствующие элементы столбца 3, умноженные на -2.   

=		0	-3	1		=
		17	1	-4
		13	-5	2

К элементам столбца 2 прибавляем соответствующие элементы столбца 3, умноженные на 3.

  

=		0	0	1		=
		17	-11	-4
		13	1	2

Разложим определитель по элементам строки 1.   

= ( -1) 1 + 3 * 1 *								17		-11			=
								13		1
=		17	-11		=
		13	1

= 17 * 1 - ( -11) * 13 =

= 17 + 143 =

= 160
Вычислим det A₂  

 

det A2 =		2	2	1		=
		2	9	-4
		6	17	2

К элементам строки 2 прибавляем соответствующие элементы строки 1, умноженные на -1.   

=		2	2	1		=
		0	7	-5
		6	17	2

К элементам строки 3 прибавляем соответствующие элементы строки 1, умноженные на -3.  

=		2	2	1		=
		0	7	-5
		0	11	-1

Разложим определитель по элементам столбца 1.   

= ( -1) 1 + 1 * 2 *							7		-5		=
							11		-1
= 2 *		7	-5		=
		11	-1

= 2 * ( 7 * ( -1) - ( -5) * 11 ) =

= 2 * ( -7 + 55 ) =

= 96
Вычислим det A₃  

 

det A3 =		2	-3	2		=
		2	1	9
		6	-5	17

К элементам строки 2 прибавляем соответствующие элементы строки 1, умноженные на -1.   

=		2	-3	2		=
		0	4	7
		6	-5	17

К элементам строки 3 прибавляем соответствующие элементы строки 1, умноженные на -3.   

=		2	-3	2		=
		0	4	7
		0	4	11

Разложим определитель по элементам столбца 1.   

= ( -1) 1 + 1 * 2 *							4		7		=
							4		11
= 2 *		4	7		=
		4	11

= 2 * ( 4 * 11 - 7 * 4 ) =

= 2 * ( 44 - 28 ) =

= 32