Высшая математика 3 вариант. КР матем - 1 курс. Задача Решить систему уравнений методом Крамера, методом Гаусса, матричным методом
 Скачать 1.45 Mb. Скачать 1.45 Mb.
|
|
Задача 4. Решить матричное уравнение и выполнить проверку. 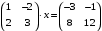 Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B. Вычислим определитель матрицы А: ∆ = 1*3 - 2*(-2) = 7 Определитель матрицы А равен detA=7 Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B. Найдем обратную матрицу A-1. Транспонированная матрица AT.
Алгебраические дополнения A11 = (-1)1+1·3 = 3; A12 = (-1)1+2·-2 = 2; A21 = (-1)2+1·2 = -2; A22 = (-1)2+2·1 = 1; Обратная матрица A-1.
Матрицу Х ищем по формуле: X = A-1·B
Ответ:
Задача №5. Решить матричные уравнения и выполнить проверку. а) 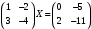 Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B. Вычислим определитель матрицы А: ∆ = 1*(-4) - 3*(-2) = 2 Определитель матрицы А равен detA=2 Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B. Найдем обратную матрицу A-1. Транспонированная матрица AT.
Алгебраические дополнения A11 = (-1)1+1·-4 = -4; A12 = (-1)1+2·-2 = 2; A21 = (-1)2+1·3 = -3; A22 = (-1)2+2·1 = 1; Обратная матрица A-1.
Матрицу Х ищем по формуле: X = A-1·B
Ответ:
|
