Высшая математика 3 вариант. КР матем - 1 курс. Задача Решить систему уравнений методом Крамера, методом Гаусса, матричным методом

• Название: Задача Решить систему уравнений методом Крамера, методом Гаусса, матричным методом
• Анкор: Высшая математика 3 вариант
• Дата: 01.12.2022
• Размер: 1.45 Mb.
• Имя файла: КР матем - 1 курс.docx
• Тип: Задача; #823190
• страница: 2 из 4

Ответ:

x₁ = det A₁ / det A = 160/32 = 5
x₂ = det A₂ / det A = 96/32 = 3
x₃ = det A₃ / det A = 32/32 = 1

Метод Гаусса: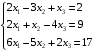

		2	x1	-	3	x2	+		x3	=	2
		2	x1	+		x2	-	4	x3	=	9
		6	x1	-	5	x2	+	2	x3	=	17

К уравнению 2 прибавляем уравнение 1, умноженное на -1.   

		2	x1	-	3	x2	+		x3	=	2
					4	x2	-	5	x3	=	7
		6	x1	-	5	x2	+	2	x3	=	17

К уравнению 3 прибавляем уравнение 1, умноженное на -3.  

		2	x1	-	3	x2	+		x3	=	2
					4	x2	-	5	x3	=	7
					4	x2	-		x3	=	11

К уравнению 3 прибавляем уравнение 2, умноженное на -1.  

		2	x1	-	3	x2	+		x3	=	2
					4	x2	-	5	x3	=	7
								4	x3	=	4

Из уравнения 3 системы найдем значение переменной x₃.
4 x₃ = 4

x₃ = 1
Из уравнения 2 системы найдем значение переменной x₂.
4 x₂ - 5 x₃ = 7

4 x₂ = 7 + 5 x₃

4 x₂ = 7 + 5 * ( 1 )

x₂ = 3
Из уравнения 1 системы найдем значение переменной x₁.
2 x₁ - 3 x₂ + x₃ = 2

2 x₁ = 2 + 3 x₂ - x₃

2 x₁ = 2 + 3 * ( 3 ) - ( 1 )

x₁ = 5
Ответ:
x₁ = 5

x₂ = 3

x₃ = 1

Матричный метод:

 Вычислим det A используя элементарные преобразования определителя.

det A =		2	-3	1		=
		2	1	-4
		6	-5	2

К элементам строки 3 прибавляем соответствующие элементы строки 1, умноженные на -2.

 

=		2	-3	1		=
		2	1	-4
		2	1	0

К элементам столбца 1 прибавляем соответствующие элементы столбца 2, умноженные на -2.

=		8	-3	1		=
		0	1	-4
		0	1	0

Разложим определитель по элементам строки 3.   

= ( -1) 3 + 2 * 1 *							8		1		=
							0		-4
= -		8	1		=
		0	-4

= - ( 8 * ( -4) - 1 * 0 ) =

= - ( -32 + 0 ) =

= 32
2. Вычислим det A используя разложение по элементам строки 1.

det A =		2	-3	1		=
		2	1	-4
		6	-5	2

Разложим определитель по элементам строки 1.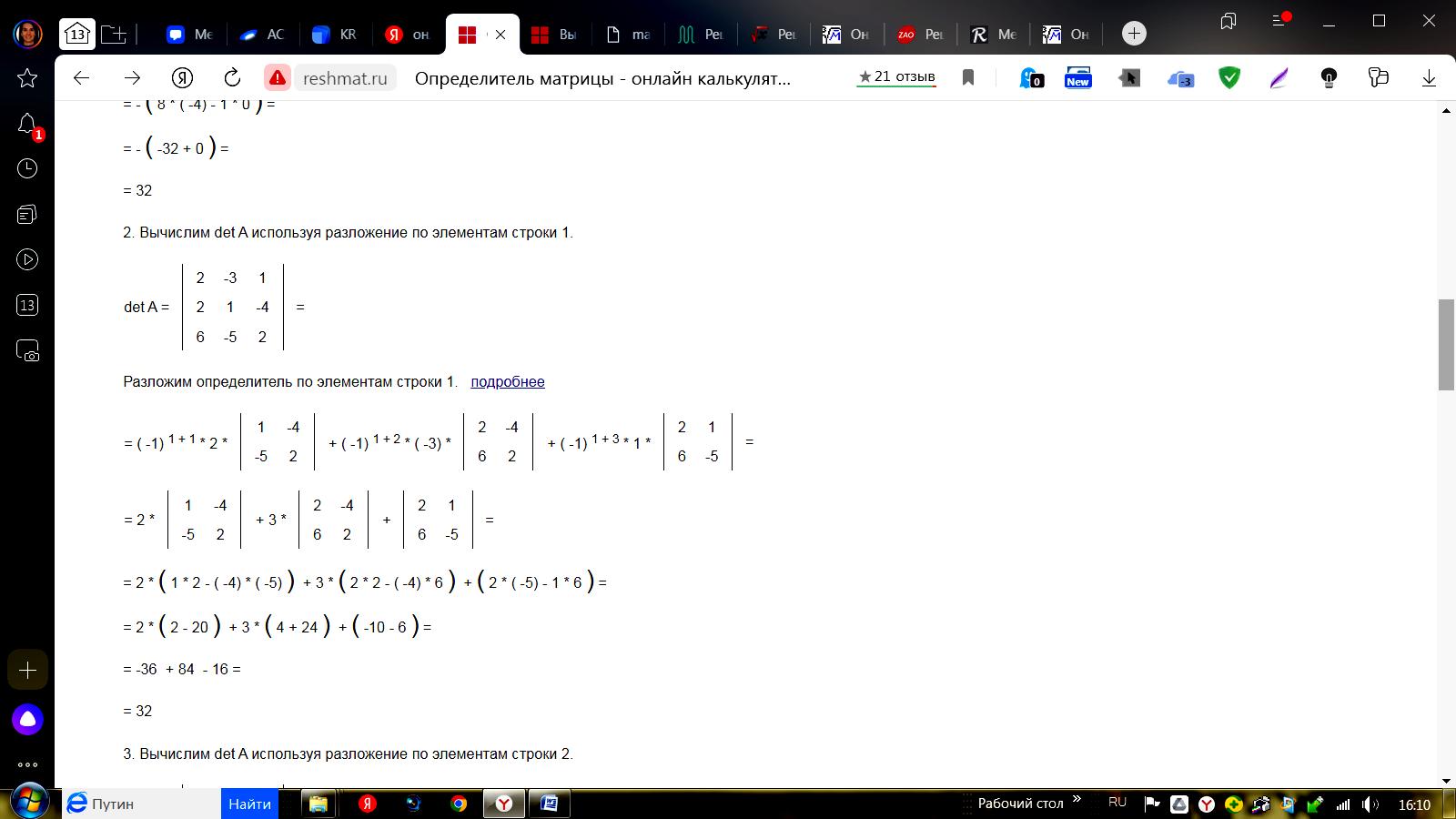  

3. Вычислим det A используя разложение по элементам строки 2.

det A =		2	-3	1		=
		2	1	-4
		6	-5	2

Разложим определитель по элементам строки 2.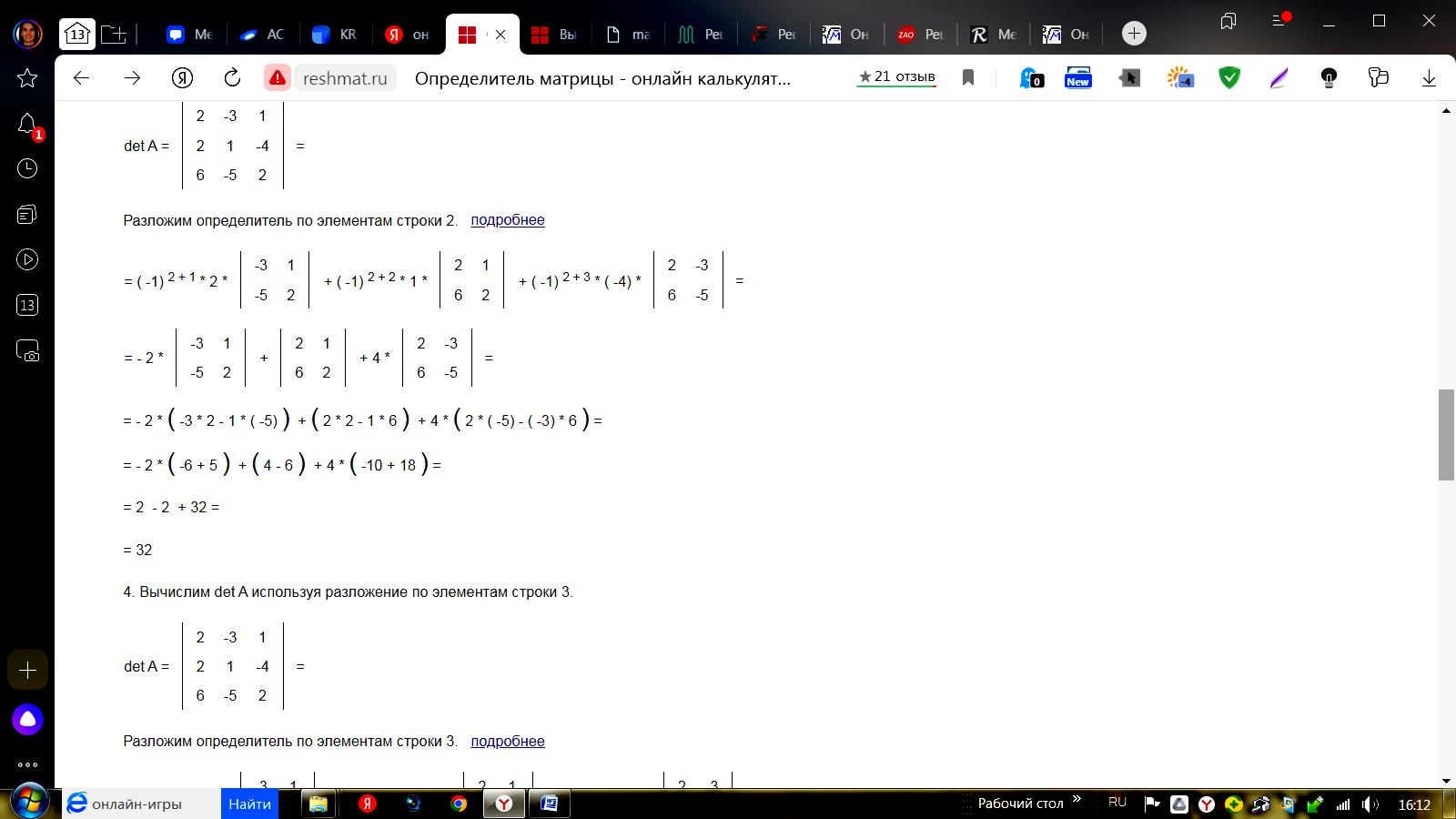   


4. Вычислим det A используя разложение по элементам строки 3.

det A =		2	-3	1		=
		2	1	-4
		6	-5	2

Разложим определитель по элементам строки 3.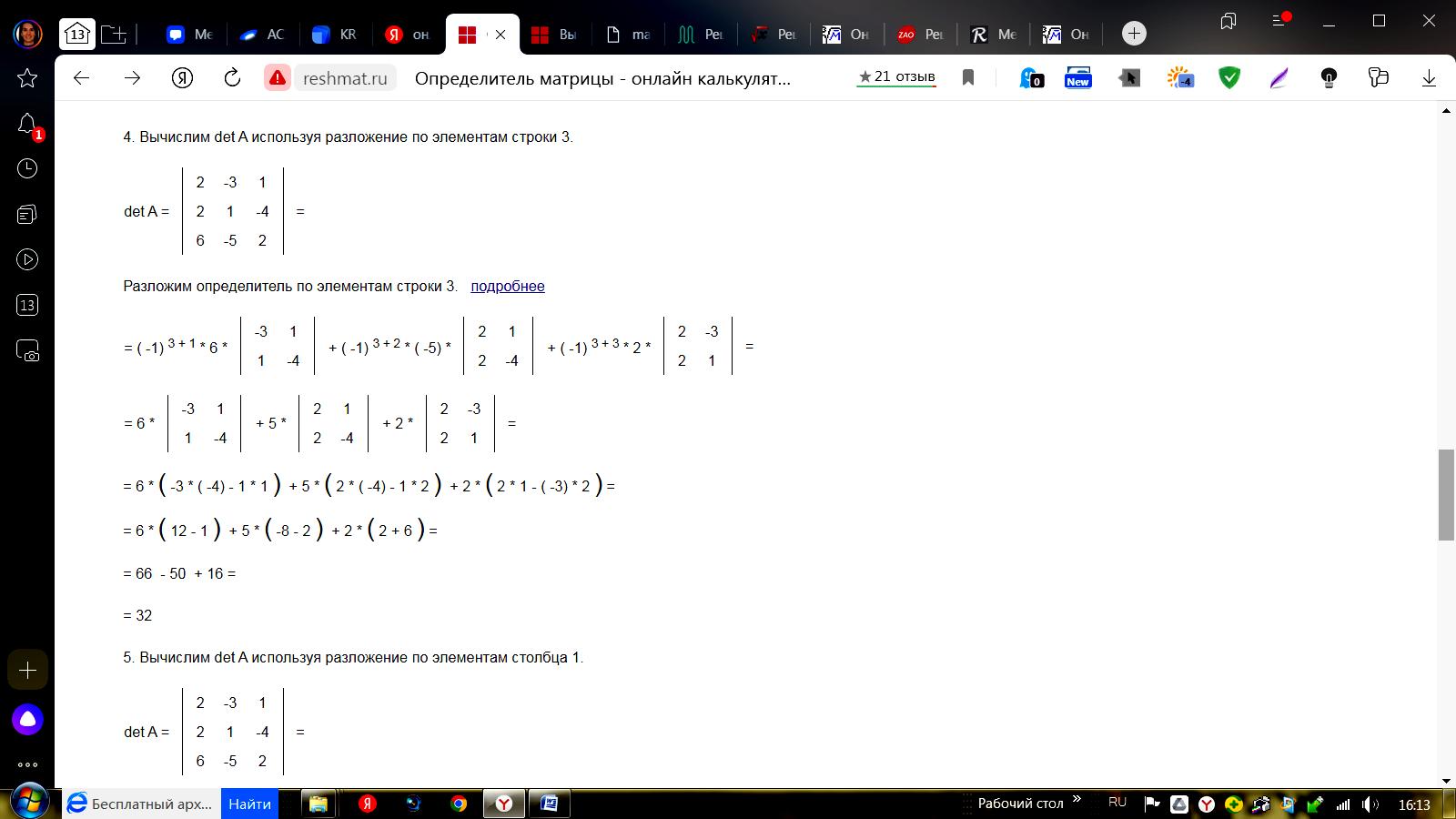   




5. Вычислим det A используя разложение по элементам столбца 1.

det A =		2	-3	1		=
		2	1	-4
		6	-5	2

Разложим определитель по элементам столбца 1.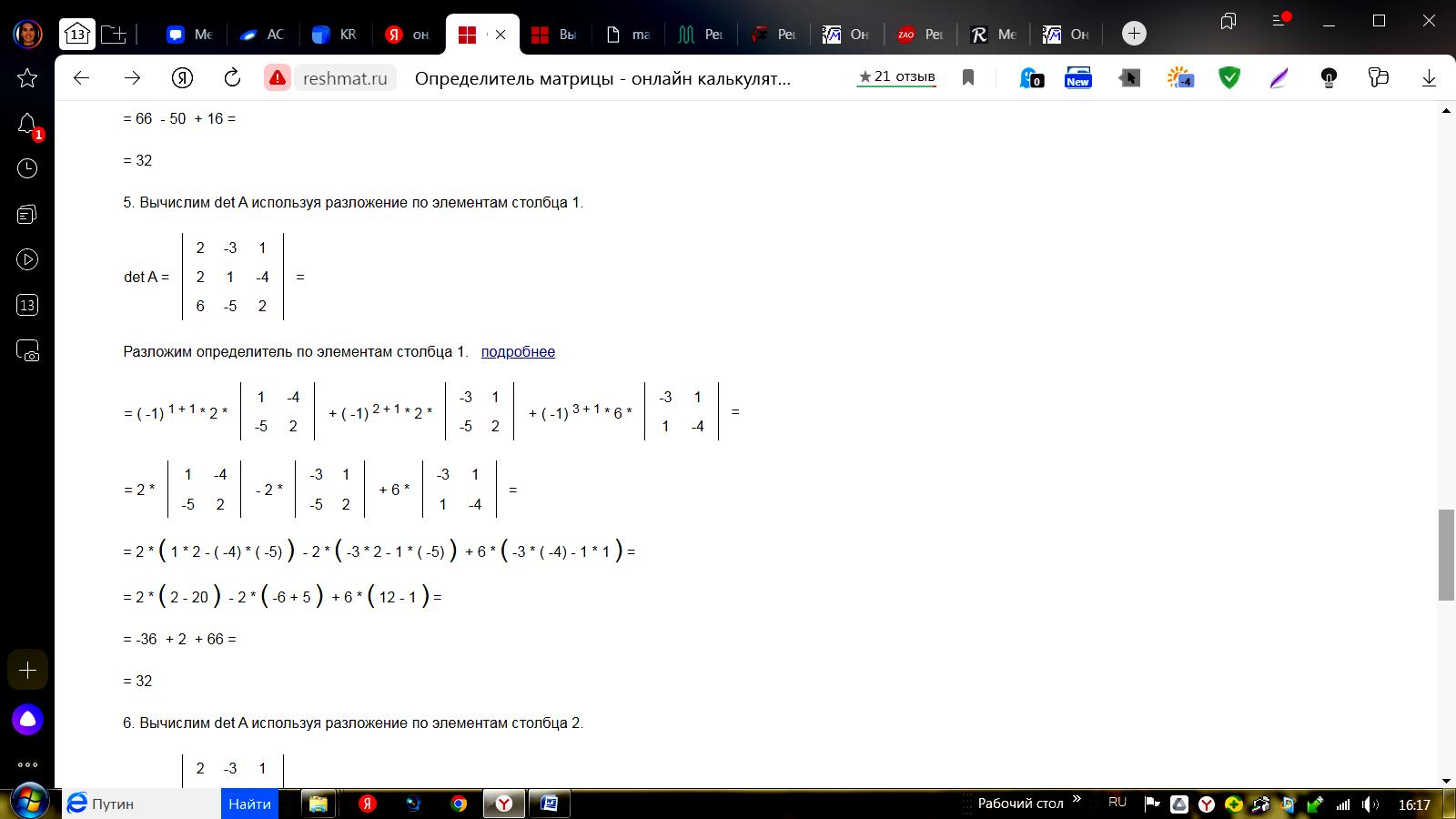  

6. Вычислим det A используя разложение по элементам столбца 2.

det A =		2	-3	1		=
		2	1	-4
		6	-5	2

Разложим определитель по элементам столбца 2.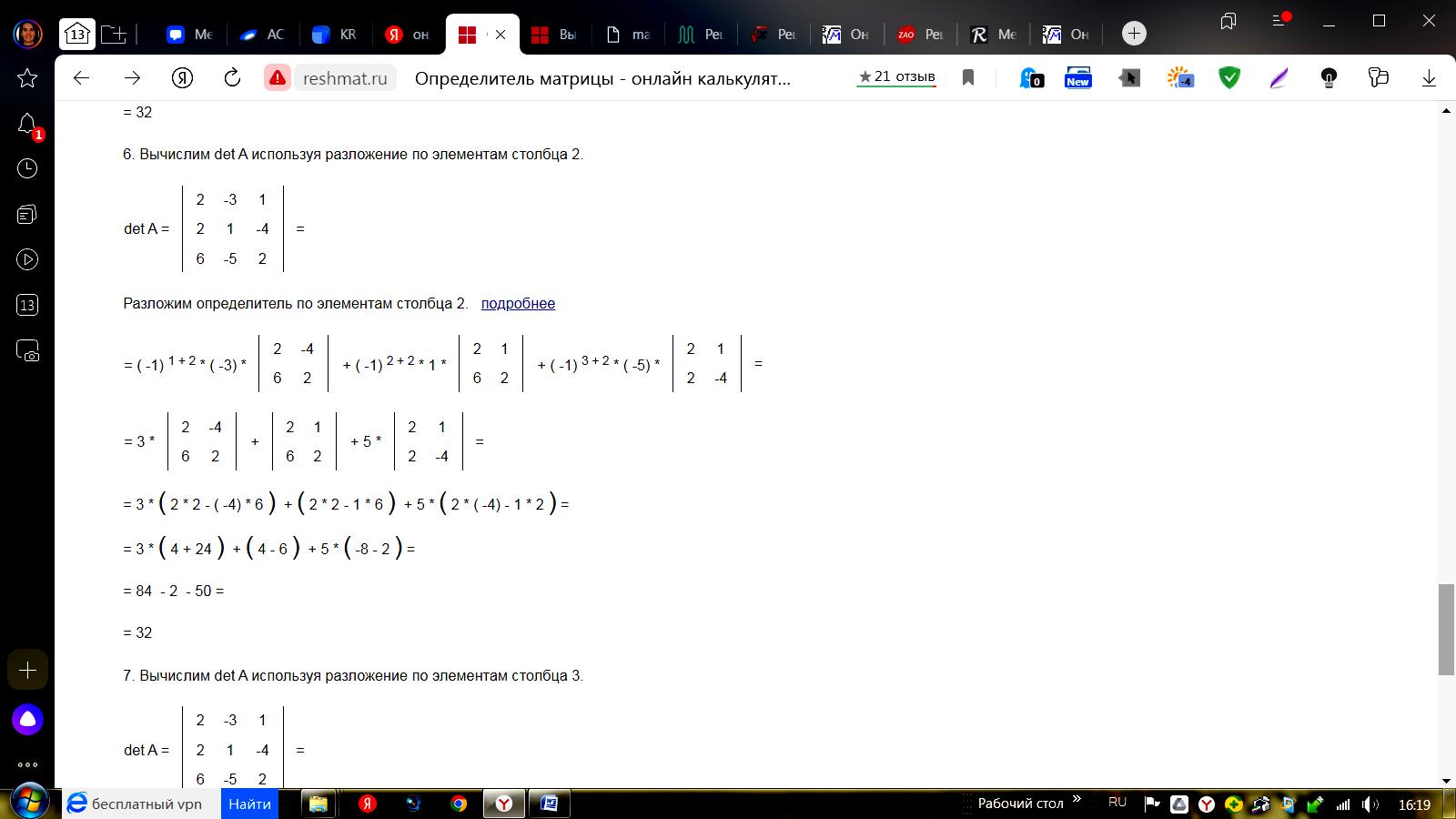

  


7. Вычислим det A используя разложение по элементам столбца 3.

det A =		2	-3	1		=
		2	1	-4
		6	-5	2

Разложим определитель по элементам столбца 3.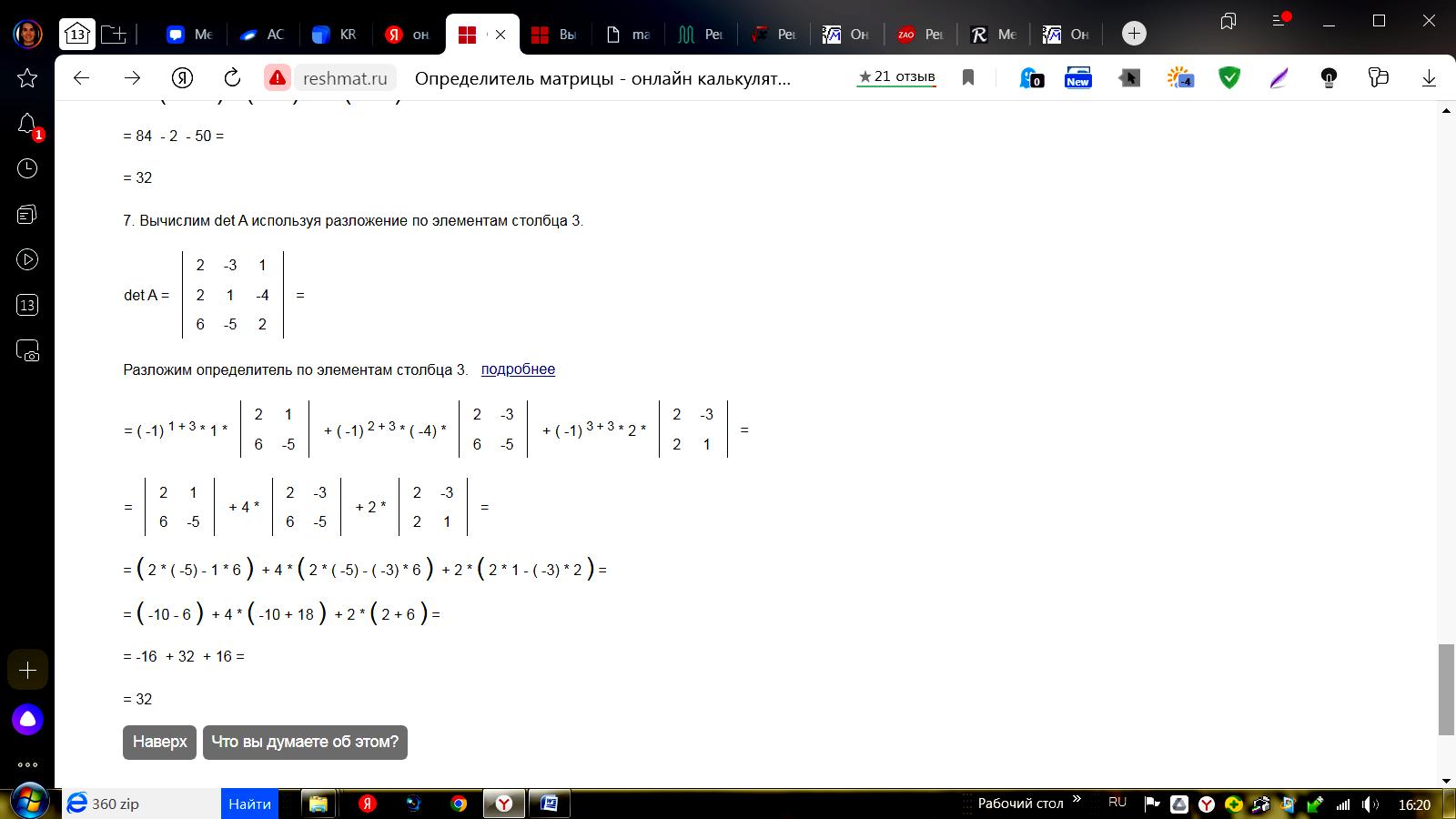