Высшая математика 3 вариант. КР матем - 1 курс. Задача Решить систему уравнений методом Крамера, методом Гаусса, матричным методом

• Название: Задача Решить систему уравнений методом Крамера, методом Гаусса, матричным методом
• Анкор: Высшая математика 3 вариант
• Дата: 01.12.2022
• Размер: 1.45 Mb.
• Имя файла: КР матем - 1 курс.docx
• Тип: Задача; #823190
• страница: 3 из 4

Задача 2. Вычислить:

3.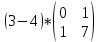

Решение: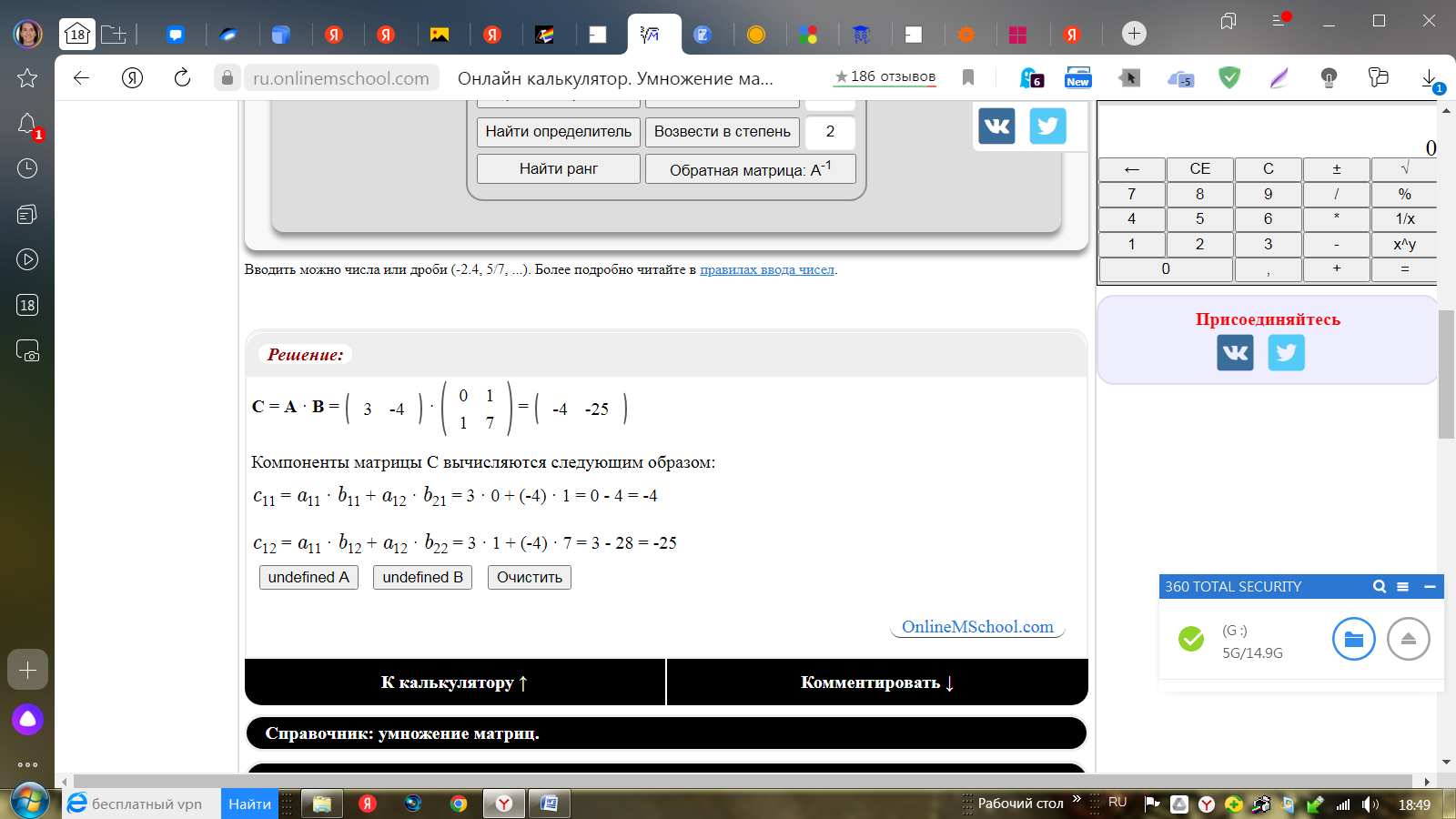



Компоненты матрицы С вычисляются следующим образом:

c₁₁ = a₁₁ · b₁₁ + a₁₂ · b₂₁ = 3 · 0 + (-4) · 1 = 0 - 4 = -4

c₁₂ = a₁₁ · b₁₂ + a₁₂ · b₂₂ = 3 · 1 + (-4) · 7 = 3 - 28 = -25

Ответ:

( -4 -25 )

Задача 3. Найти обратную матрицу, сделать проверку: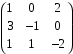



Для нахождения обратной матрицы запишим матрицу А, дописав к ней справа единичную матрицу:

	1	0	2	1	0	0
	3	-1	0	0	1	0
	1	1	-2	0	0	1

от 2; 3 строк отнимаем 1 строку, умноженую соответственно на 3; 1

	1	0	2	1	0	0
	0	-1	-6	-3	1	0
	0	1	-4	-1	0	1

2-ую строку делим на -1

	1	0	2	1	0	0
	0	1	6	3	-1	0
	0	1	-4	-1	0	1

от 3 строк отнимаем 2 строку, умноженую соответственно на 1

	1	0	2	1	0	0
	0	1	6	3	-1	0
	0	0	-10	-4	1	1

3-ую строку делим на -10

	1	0	2	1	0	0
	0	1	6	3	-1	0
	0	0	1	0.4	-0.1	-0.1

от 1; 2 строк отнимаем 3 строку, умноженую соответственно на 2; 6

	1	0	0	0.2	0.2	0.2
	0	1	0	0.6	-0.4	0.6
	0	0	1	0.4	-0.1	-0.1

Ответ:

A-1 =		0.2	0.2	0.2
		0.6	-0.4	0.6
		0.4	-0.1	-0.1

Проверка:
Проверим правильность нахождения обратной матрицы путем умножения исходной матрицы на обратную. Должны получить единичную матрицу E.

E=A*A-1=

1 0 2 3 -1 0 1 1 -2

2 2 2 6 -4 6 4 -1 -1

E=A*A^-1=

1*2+0*6+2*4	1*2+0*(-4)+2*(-1)	1*2+0*6+2*(-1)
3*2+(-1)*6+0*4	3*2+(-1)*(-4)+0*(-1)	3*2+(-1)*6+0*(-1)
1*2+1*6+(-2)*4	1*2+1*(-4)+(-2)*(-1)	1*2+1*6+(-2)*(-1)

1 0 0 0 0 10 0 0 0 10

A*A-1=

1 0 0 0 1 0 0 0 1