Комплексные числа_Пр. Решение а. Значит, б. Значит, Пример Представить в алгебраической форме числа
 Скачать 41.26 Kb. Скачать 41.26 Kb.
|
|
Комплексные числа Пример 1. Изобразить комплексные числа векторами и записать в тригонометрической и показательной формах: а) z=2+2i; б) z=-5i. Решение. а 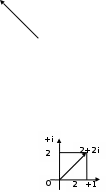 ) )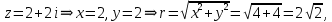 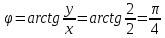 . .Значит, 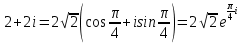 б  ) ) 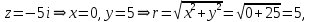 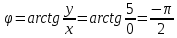 . .Значит, 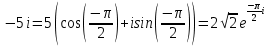 Пример 2. Представить в алгебраической форме числа: 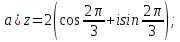 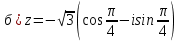 Решение. а) 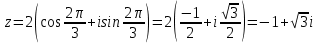 . .б) 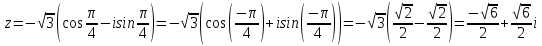 П  ример 2. Изобразить на комплексной плоскости С множества точек, удовлетворяющих следующим условиям: а) ример 2. Изобразить на комплексной плоскости С множества точек, удовлетворяющих следующим условиям: а) 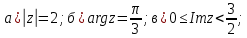 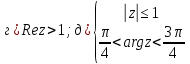 Р 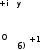 ешение. а) ешение. а)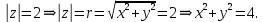 То есть множество точек, удовлетворяющих условию То есть множество точек, удовлетворяющих условию 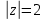 , представляет собой окружность радиуса R=2 с центром в начале координат. , представляет собой окружность радиуса R=2 с центром в начале координат.б 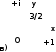 ) ) 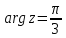 , то есть точки z лежат на луче, выходящем из точки О(0;0) под углом , то есть точки z лежат на луче, выходящем из точки О(0;0) под углом 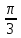 к действительной оси. к действительной оси.в) 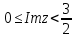 , данное неравенство определяет множество всех точек, лежащих в полосе , данное неравенство определяет множество всех точек, лежащих в полосе 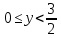 . .г   ) ) 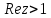 , то есть , то есть 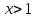 , данное условие определяет множество всех точек, расположенных справа от прямой , данное условие определяет множество всех точек, расположенных справа от прямой 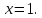 д) 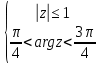 - множество точек, расположенных внутри и на границе круга - множество точек, расположенных внутри и на границе круга 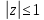 , заключённых между лучами , заключённых между лучами 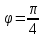 и и 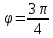 Пример 3. Найти сумму, разность, произведение и частное чисел 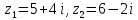 Решение. 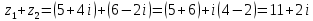 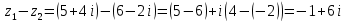 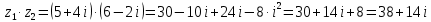 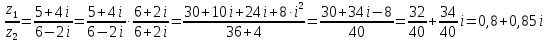 П  ример 4. Вычислить: ример 4. Вычислить: 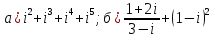 Решение. а) представим число i в тригонометрической форме 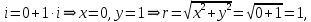 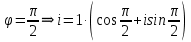 з зЗначит, 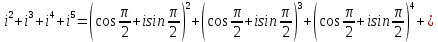 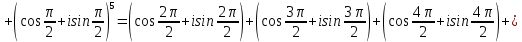 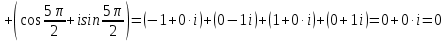 б) 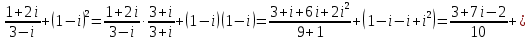 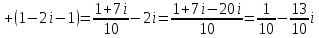 Пример 5. Найти 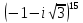 Р  ешение. Представим число ешение. Представим число 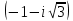 в тригонометрической форме в тригонометрической форме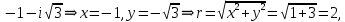 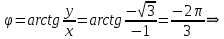 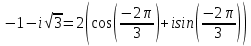 Значит, 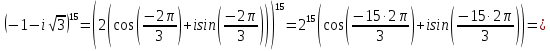 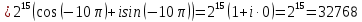 Пример 6. Найти все значения корня 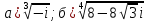 Решение. а) представим число 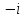 в тригонометрической форме в тригонометрической форме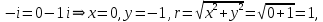  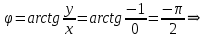 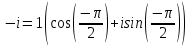 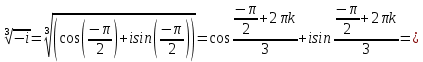 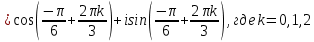 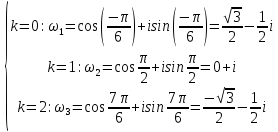 б) представим число 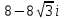 в тригонометрической форме в тригонометрической форме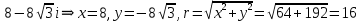  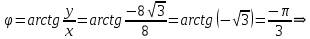 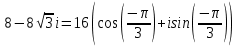 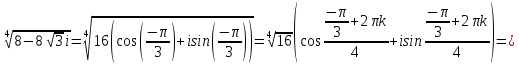 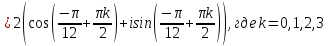 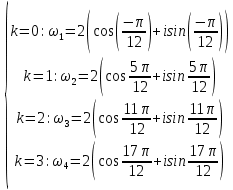 Пример 7. Найти xи y из уравнения 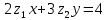 если если 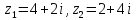 Решение. 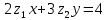 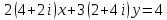 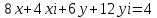 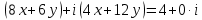 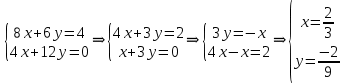 Задачи для самостоятельного решения 1) Представить в тригонометрической и алгебраической формах числа: 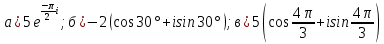 2) Изобразить на комплексной плоскости множество точек, удовлетворяющих условиям: 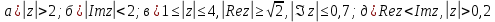 3) Найти сумму, разность, произведение и частное чисел 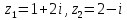 4) Вычислить: 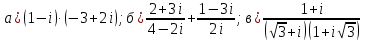 5) Найти: 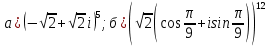 6) Найти все значения корня 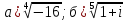 7) Найти xи y из уравнения 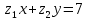 если если 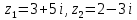 +1 |
