Контрольная работа по физической химии. физич химия(1). Решение Абсолютная температура равна Работа при изотермическом расширении идеального газа рассчитывается по уравнению
 Скачать 2.63 Mb. Скачать 2.63 Mb.
|
|
17 Один моль идеального газа, взятого при 25 С и 100 атм, расширяется обратимо и изотермически до 5 атм. Рассчитайте работу, поглощенную теплоту, изменение внутренней энергии и энтальпии Решение: Абсолютная температура равна: 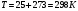 Работа при изотермическом расширении идеального газа рассчитывается по уравнению:  , где n – количество молей газа, R – молярная газовая постоянная (8,314 Дж/моль∙К), Т – абсолютная температура. , где n – количество молей газа, R – молярная газовая постоянная (8,314 Дж/моль∙К), Т – абсолютная температура.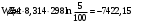 По первому закону термодинамики внутренняя энергия системы в изотермическом процессе не изменяется, то есть 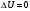 . В соответствии с этим, поглощенная теплота равна работе: . В соответствии с этим, поглощенная теплота равна работе: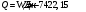 Изменение энтальпии численно равняется теплоте расширения, но с обратным знаком: 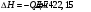 51 Для реакции, приведенной в таблице 1.3: рассчитайте стандартный тепловой эффект реакции по известным величинам стандартных теплот образования исходных веществ и продуктов реакции; определите Нт из предположения: а) с = 0; б) с = const; в) с = f (Т). определите 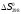 и SТ для реакции; и SТ для реакции;вычислите значение 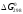 и GТ и сделайте вывод о направлении реакции в стандартных условиях и при температуре Т. и GТ и сделайте вывод о направлении реакции в стандартных условиях и при температуре Т.Термодинамические характеристики веществ приведены в таблице 1.4
Решение: 1) Тепловой эффект при стандартных условиях составит: 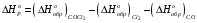 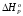 = - 223 – 0 + 110,6 = - 112,4 кДж/моль = - 112400 Дж/моль. = - 223 – 0 + 110,6 = - 112,4 кДж/моль = - 112400 Дж/моль.Аналогично рассчитываются ∆СР, 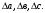 ∆СР= 60,67 – 33,96 – 29,13 = -2,42 Дж/(моль∙К); ∆а = 67,16 – 36,9 – 28,43 = 1,83; ∆b = (12,11 – 1,05 – 4,1)∙10-3 = 6,96∙10-3; ∆с’ = (- 9,03 + 2,52 + 0,46)∙105 = - 6,05∙105 2) а) с = 0; 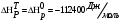 б) с = const; 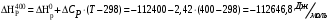 в) с = f (Т). Тепловой эффект по точному уравнению Кирхгофа при 400 К рассчитывается по уравнению: 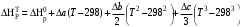 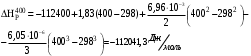 3) При стандартных условиях энтропия рассчитывается также по закону Гесса: 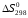 = 289,2 – 223,1 – 197,7 = - 131,6 Дж/моль; = 289,2 – 223,1 – 197,7 = - 131,6 Дж/моль;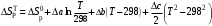 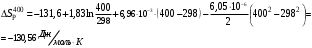 4) Энергию Гиббса рассчитывают по уравнению: 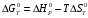 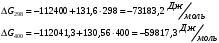 Так как энергия Гиббса реакции имеет отрицательное значение, реакция протекает в прямом направлении в стандартных условиях и при нагревании. Таблица 1.4 Термодинамические характеристики веществ
55. Однокомпонентные гетерогенные системы. Диаграмма состояния воды Примером однокомпонентной системы может служить любое простое вещество, а также химическое соединение, обладающее строго определенным составом во всех трех агрегатных состояниях, которые могут находиться в равновесии друг с другом попарно либо все вместе в зависимости от параметров состояния:  Диаграмма состояния однокомпонентной системы представляет собой геометрический образ, выраженный линиями попарного равновесия в координа- тах Р – Т (рис. 1) 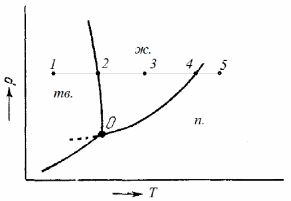 Рис 1. Диаграмма состояния воды при низких давлениях насыщенного пара Линии фазовых равновесий отделяют друг от друга три поля, отвечающие стабильному существованию твердой, жидкой или паровой фазы. Все фигуративные точки, принадлежащие одному полю (точки 1, 3 и 5), отвечают однофазному состоянию (Ф = 1). Согласно правилу фаз Гиббса, система в любой такой точке обладает двумя степенями свободы: С = К + N – Ф = 1 + 2 – 1 = 2. Это означает, что в пределах данного фазового поля одновременное произвольное изменение двух параметров состояния – Р и Т – не вызывает нарушения фазового равновесия (число фаз не изменяется). С другой стороны, изменение температуры при изобарном переходе из состояния 1 в состояние 5 приводит к снижению энергии Гиббса системы в соответствии с уравнением 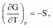 где S – энтропия фазы. Для паровой, жидкой и твердой фаз чистого вещества справедливо соотношение Sпар >> Sж > Sтв. Графически это проявляется на температурной зависимости энергии Гиббса так, что G,T-кривые для двух фаз будут пересекаться в некоторых точках, отвечающих равенствам 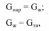 т.е. равновесию соответствующих фаз (рис. 2). Следовательно, точки пересечения G,T-зависимостей отвечают температурам плавления и кипения вещества. При температурах Т < Тпл соблюдаются условия 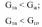 поэтому термодинамически более устойчивой является твердая фаза. При условии Тпл < Т < Ткип справедливы неравенства 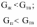 а потому в таких условиях стабильной будет уже жидкая фаза.  Рис. 2. Определение фиксированного положения температур двухфазного равновесия в однокомпонентной системе. Наконец, при температурах Т > Ткип 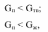 и устойчивой будет уже газообразная фаза. Таким образом, фигуративные точки 2 и 4, лежащие на кривых плавления и испарения, отвечают изобарному двухфазному равновесию. Равновесие в любой точке на кривой фазовой диаграммы однокомпонентной системы является моновариантным: Ф = 2, С = 1 + 2 – 2 = 1. Это означает, что произвольно может быть изменен лишь один параметр состояния системы: либо температура, либо давление. Вблизи тройной точки кривая возгонки будет возрастать более круто, чем кривая испарения. Переход охлаждаемой жидкости в кристаллическое состояние не всегда начинается точно при температуре замерзания. Если жидкость не содержит хотя бы мельчайших твердых частиц, которые могут служить центрами кристаллизации, то имеет место переохлаждение, и выделение кристаллов начинается при более низкой температуре (пунктир на диаграмме состояния, рис. 1). Процесс кристаллизации сопровождается выделением теплоты, вследствие чего температура системы вновь повышается и достигает равновесной температуры замерзания, при которой и протекает весь остальной процесс кристаллизации. Переохлажденная жидкость термодинамически неустойчива по отношению к кристаллической фазе, находящейся при той же температуре, и является примером метастабильного состояния. 122. Для реакции (CH3)3CBr + H2O (CH3)3COH + HBr получены экспериментальные данные по зависимости текущей концентрации исходного вещества от времени:
Найдите порядок реакции дифференциальным методом, константу скорости и период полураспада. Решение: По закону действия масс, скорость химической реакции при постоянной температуре определяется выражением: 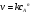 , где k – константа скорости реакции, сА – начальная концентрация вещества А, n – порядок реакции по веществу А. , где k – константа скорости реакции, сА – начальная концентрация вещества А, n – порядок реакции по веществу А.Пролагарифмируем это выражение: 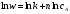 Запишем кинетические данные в координатах lnw-lnсА, причем скорость реакции определим через конечные изменения концентраций и времени: 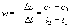 . .(Концентрацию вещества иногда обозначают не квадратными скобками, а буквой c). По этой приближенной формуле скорость лучше определять в середине временного интервала: t = (t1 + t2)/2. Концентрацию в этот момент времени определим как полусумму значений на границах интервала: c = (c1 + c2)/2. Сведем полученные данные в таблицу (учтем, что c А = 10,39 моль/л при t = 0):
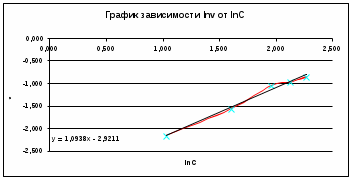 График зависимости lnw-lnc представляет собой прямую, описываемую уравнением y = 1.0938x – 2,9211. Тангенс угла наклона прямой равен 1.0938, поэтому реакция имеет первый порядок. Константу скорости реакции определяем из уравнения: 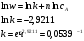 Период полураспада для реакции первого порядка равен: 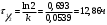 140. Константа скорости инактивация пенициллина равна 0,02 ч-1 при 310 К. Вычислите период полупревращения этой реакции. Какая часть пенициллина разложится через 10 часов? Решение: Инактивация пенициллина – реакция первого порядка. Период полупревращения находим по уравнению: 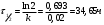 Это время, за которое превратится половина от начального количества пенициллина. Согласно кинетическому уравнению для реакции первого порядка, отношение концентрации пенициллина спустя 10 часов к начальной концентрации пенициллина можно выразить так: 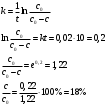 В итоге, получаем, что спустя 10 часов разложится 18% всего пенициллина. 176, 177. Определите значения константы Михаэлиса, максимальной скорости и параметр аЕ для гидролиза метилового эфира N - ацетил L – валина, катализированного – химотрипсином по следующим экспериментальным данным:
Концентрация фермента во всех случаях постоянна и равна 10-5 моль/л. Решение: Ферментативная реакция: 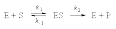 Уравнение Михаэлиса-Ментен для описания кинетики ферментативной реакции имеет вид: 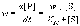 , где , где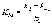 - константа Михаэлиса. Эта константа равна концентрации субстрата, при которой скорость реакции равна половине максимальной скорости. Типичные значения KM - от 10-6 до 10-1 моль/л. Построим график зависимости v от v /[S]: 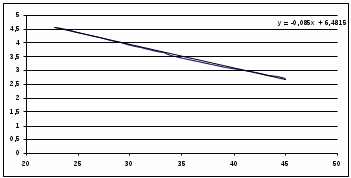 Получили прямую, уравнение которой 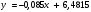 Точки пересечения с осями имеют координаты:(0;vmax) для оси ординат, (vmax/KM;0) для оси абсцисс. Первая точка пересечения дает значение vmax = 6,48∙10-6 моль/(л.с). Вторая точка позволяет найти константу Михаэлиса: vmax/KM = 76,25∙10-6 с-1, KM = 6,48∙10-6 /76,25∙10-6 = 0,085 моль/л. Параметр аЕ = 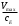 = 6,48∙10-6/ 10-5 = 0,648 с-1. = 6,48∙10-6/ 10-5 = 0,648 с-1.194. Эквивалентная электропроводность бесконечно разбавленных растворов соляной кислоты, хлорида натрия и ацетата натрия при 298 К равна, соответственно, 425, 128,1 и 91 См см2/моль. Какова эквивалентная электропроводность бесконечно разбавленного раствора уксусной кислоты при данной температуре? Решение: По уравнению Кольрауша для эквивалентной электропроводности бесконечно разбавленных растворов (эквивалентная электропроводность есть сумма электропроводностей катиона и аниона):  Составим систему уравнений и выразим сумму электропроводностей иона водорода и ацетат иона, это и будет эквивалентная электропроводность уксусной кислоты: 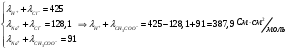  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

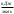
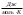
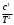 + сТ2,
+ сТ2,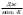
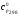 ,
,