Главная страница
Навигация по странице:

  • m

  • н тервальный статистический ряд распределения

    		•

    Примеры решения задач по теории вероятностей. Решение АУ человека опухоль легких ВУ человека плеврит


    Скачать 127.5 Kb.
    НазваниеРешение АУ человека опухоль легких ВУ человека плеврит
    Дата18.03.2018
    Размер127.5 Kb.
    Формат файлаdoc
    Имя файлаПримеры решения задач по теории вероятностей.doc
    ТипРешение
    #38802

    Задание 1. При обследовании 250 человек с помощью флюорографии были выявлены следующие заболевания: 7 человек – опухоль легких, у 3 человек – плеврит, у 5 –остаточные явления после воспаления легких. Найти вероятность этих заболеваний, выявленных с помощью флюорографии.
    Решение:

    А={У человека опухоль легких};

    В={У человека плеврит};

    С={У человека остаточные явления после воспаления легких}.
    По классической формуле вероятности , где m – число появлений события F, n – число испытаний найдем вероятность для каждого из заболеваний:

    ;

    ;

    .

    Ответ: 0,028; 0,012; 0,02.
    Задание 2. На некоторой фабрике машина А производит 40% всей продукции, а машина В – 60%. В среднем 9 единиц из 1000 единиц продукции, произведенных машиной А, оказывается браком, а у машины В – брак 2 единицы из 500. Некоторая единица продукции, выбранная случайным образом из дневной продукции, оказалась браком. Какова вероятность того, что она произведена на машине В?
    Решение:
    А1={Продукция, произведенная машиной А}, ;

    А2={Продукция, произведенная машиной В}, .

    С={Бракованная продукция};

    ;

    .

    По формуле Байеса находим вероятность того, что бракованная единица продукции произведена на машине В:
    .

    Ответ: 0,4.
    Задание 3. Вероятность того, что покупателю требуется обувь 41-го размера, равна 0,2. Найти вероятность того, что среди 100 покупателей потребуют обувь 41-го размера: а) 25 человек; б) от 10 до 30 человек; в) не более 30 человек; г) не менее 35 человек.
    Решение:

    Так как количество независимых испытаний достаточно большое и применение формулы Бернулли трудоемко, то применим локальную и интегральную теоремы Муавра-Лапласа. Проверяем актуальность применения формулы, чтобы погрешность вычислений была не большой необходимо выполнение неравенства npq>10, у нас npq=100*0.2*0.8=16 >10.

    Формула локальной теоремы Муавра-Лапласа , где , - функция Гаусса, которую определяем по таблице.

    Формула интегральной теоремы Муавра-Лапласа , где 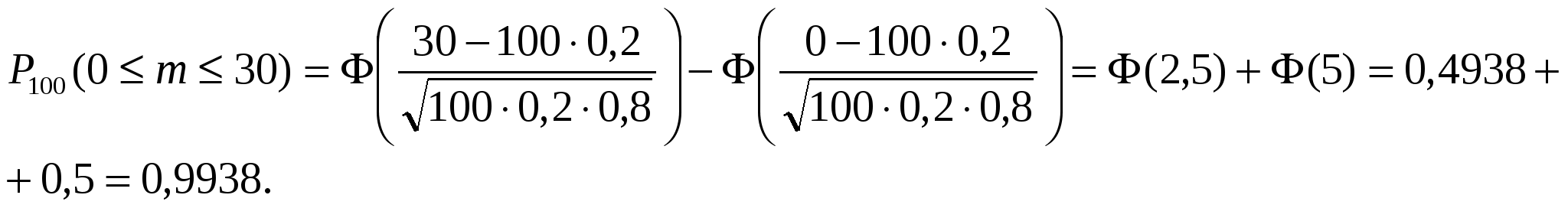, , - функция Лапласа, которую определяем по таблице.
    а) .

    б)

    в)

    г)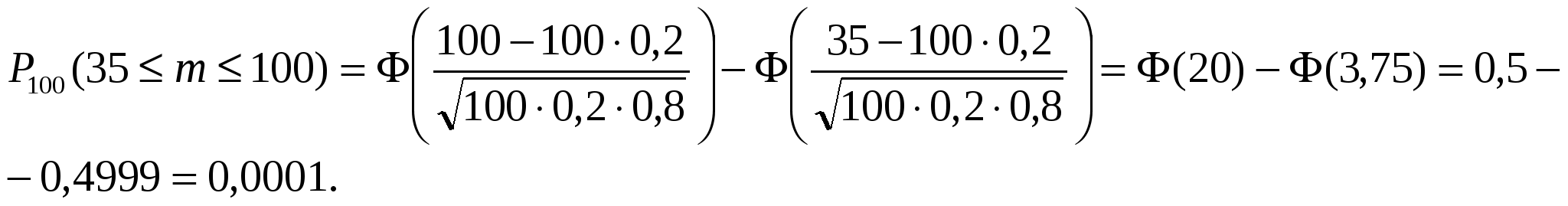
    Задание 4. Для выяснения эффективности некоторого препарата исследовали некоторый показатель жизнедеятельности у животных двух групп. Среднее значение этого показателя для 20 животных опытной группы (т.е. той группы, в которой применялся препарат) составило при исправленной выборочной дисперсии . Для 18 животных контрольной группы соответствующие показатели оказались равными и . В предположении справедливости нормального закона распределения изучаемого показателя у животных как опытной, так и контрольной групп при уровне значимости р = 0,05 определить: позволяют ли проведенные исследования утверждать, что данный препарат действительно оказывает определенное воздействие на изучаемый показатель жизнедеятельности животных?

    Решение:

    Найдем tэксп и tкрит, если:

    1) |tэксп.| > tкрит., то при уровне значимости р нулевую гипотезу отвергается в пользу конкурирующей и наблюдаемое различие в выборочных средних считается проявлением различия соответствующих генеральных средних.

    2) |tэксп.| < tкрит., то при этом же уровне значимости нулевая гипотеза считается согласующейся с результатами наблюдений, т.е. различие в выборочных средних считается незначимым.

    Нулевая гипотеза, которую следует проверить, состоит в равенстве средних значений показателя жизнедеятельности у животных в двух группах животных, первая из которых опытная группа, вторая — контрольная группа.

    Найдем экспериментальное значение критерия: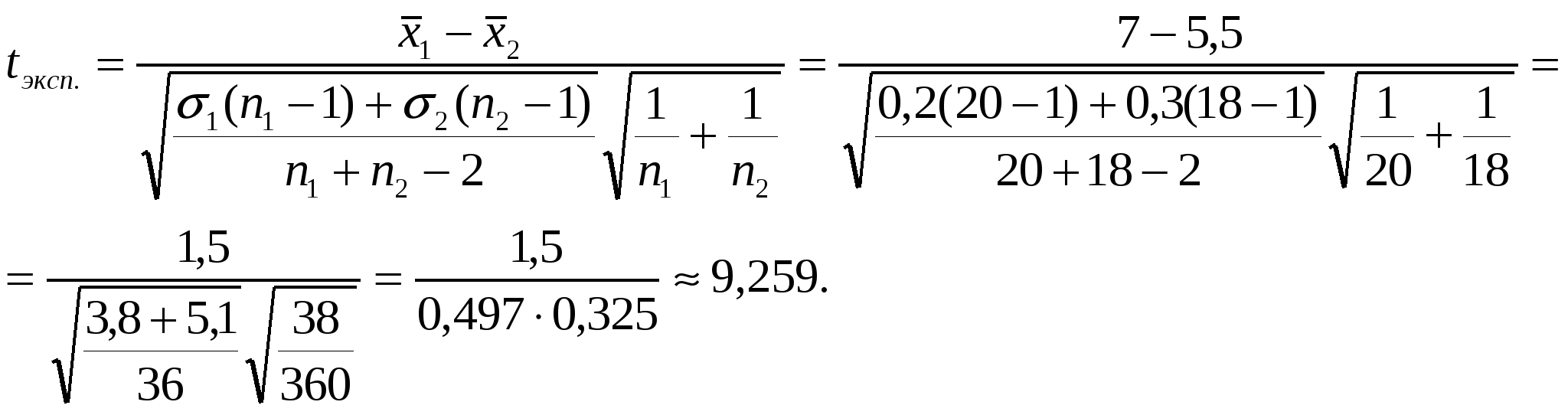



    k=20+18-2=36.

    По таблице критических значений распределения Стьюдента (двусторонняя критическая область) — значение

    tкрит.(0,05; 36) = 2,028.

    Поскольку |tэксп.| > tкрит., то при уровне значимости р = 0,05 нулевая гипотеза отвергается, а значит можно сделать вывод, что данный препарат оказывает воздействие на изучаемый показатель жизнедеятельности животных.

    Задание 5. Из продукции, произведенной фармацевтической фабрикой за месяц, случайным образом отобраны 15 коробочек некоторого гомеопатического препарата, количество таблеток в которых оказалось равным соответственно 50, 51, 48, 52, 50, 49, 50, 47, 50, 51, 49, 50, 52, 48, 49. Найти статистический интервальный ряд распределения и построить гистограмму относительных частот.
    Решение:

    Определим количество интервалов по формуле Стерджеса: .

    .

    Определим величину шага интервала .

     Получаем интервальный статистический ряд распределения:

    Интервалы
    [47-48)
    [48-49)
    [49-50)
    [50-51)
    [51-52]

    Частоты ni
    1
    2
    3
    5
    4

    Относительные частоты ωi=ni/n
    1/15
    2/15
    3/15
    5/15
    4/15


    Строим гистограмму относительных частот: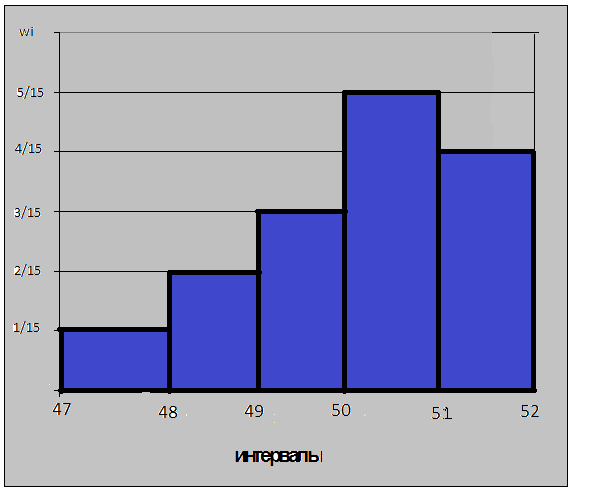


    Задание 6. Изучалась зависимость между минутным объемом сердца Y (л/мин) и средним давлением в левом предсердии Х (мм рт. ст.). Результаты наблюдений приведены в таблице в виде двумерной выборки объема 5:

    Х
    4,8
    6,4
    9,3
    11,2
    17,7

    Y
    0,4
    0,69
    1,29
    1,64
    2,4

    Требуется: 1) Вычислить выборочный коэффициент корреляции между переменными Y и Х;

    2) Написать уравнение линейной регрессии Y на Х.

    Решение:

    1) Составим расчетную таблицу:

    №
    Xi
    Yi
    Xi*Yi
    Xi2
    Yi2

    1
    4,8
    0,4
    1,92
    23,04
    0,16

    2
    6,4
    0,69
    4,416
    40,96
    0,4761

    3
    9,3
    1,29
    11,997
    86,49
    1,6641

    4
    11,2
    1,64
    18,368
    125,44
    2,6896

    5
    17,7
    2,4
    42,48
    313,29
    5,76

    Ʃ
    49,4
    6,42
    79,181
    589,22
    10,7498


    Вычислить выборочный коэффициент корреляции между переменными Y и Х вычислим по формуле:

    .

    Получаем: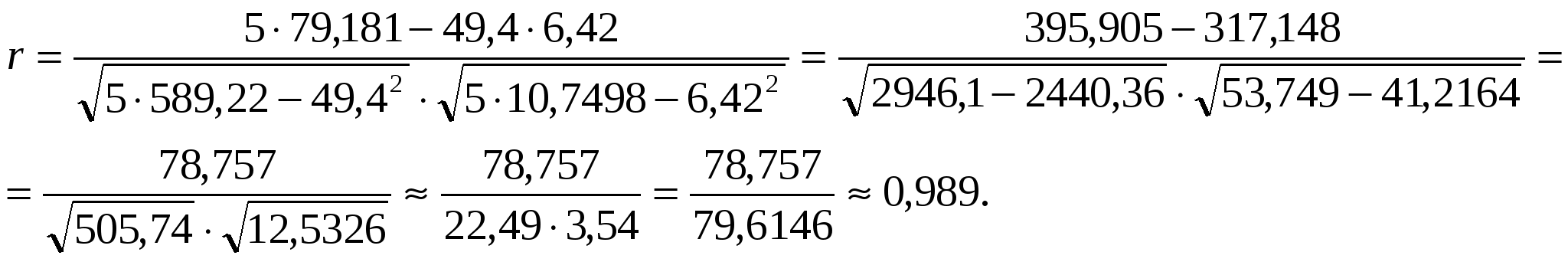



    2) Вычисляем средние арифметические значения признаков Х и Y





    Находим величины которые фигурируют в уравнении регрессии - a, b:





    Уравнение регрессии Y на X записываем по формуле: y=0,156*x-0,257.

    написать администратору сайта