Задание 23 ЕГЭ по информатике. Решение. Решение Будем рассматривать совокупность условий как систему логических уравнений, каждое из которых является истинным (1)

• Название: Решение Будем рассматривать совокупность условий как систему логических уравнений, каждое из которых является истинным (1)
• Анкор: Задание 23 ЕГЭ по информатике
• Дата: 20.02.2023
• Размер: 159.5 Kb.
• Имя файла: Решение.doc
• Тип: Решение; #946764

Задание.

Сколько существует различных наборов значений логических переменных , которые удовлетворяют всем перечисленным условиям?

Решение

Будем рассматривать совокупность условий как систему логических уравнений, каждое из которых является истинным (=1):



Упростим выражения с учетом того, что в левой части находится отрицание выражения. Применим отрицание к обеим частям и к левой – закон двойного отрицания. Получим:



Заметим, что выражения состоят из однотипных конъюнкций, причем каждая переменная входит только в одно выражение. Для упрощения уравнений введем новые переменные:



Тогда систему можно записать в виде: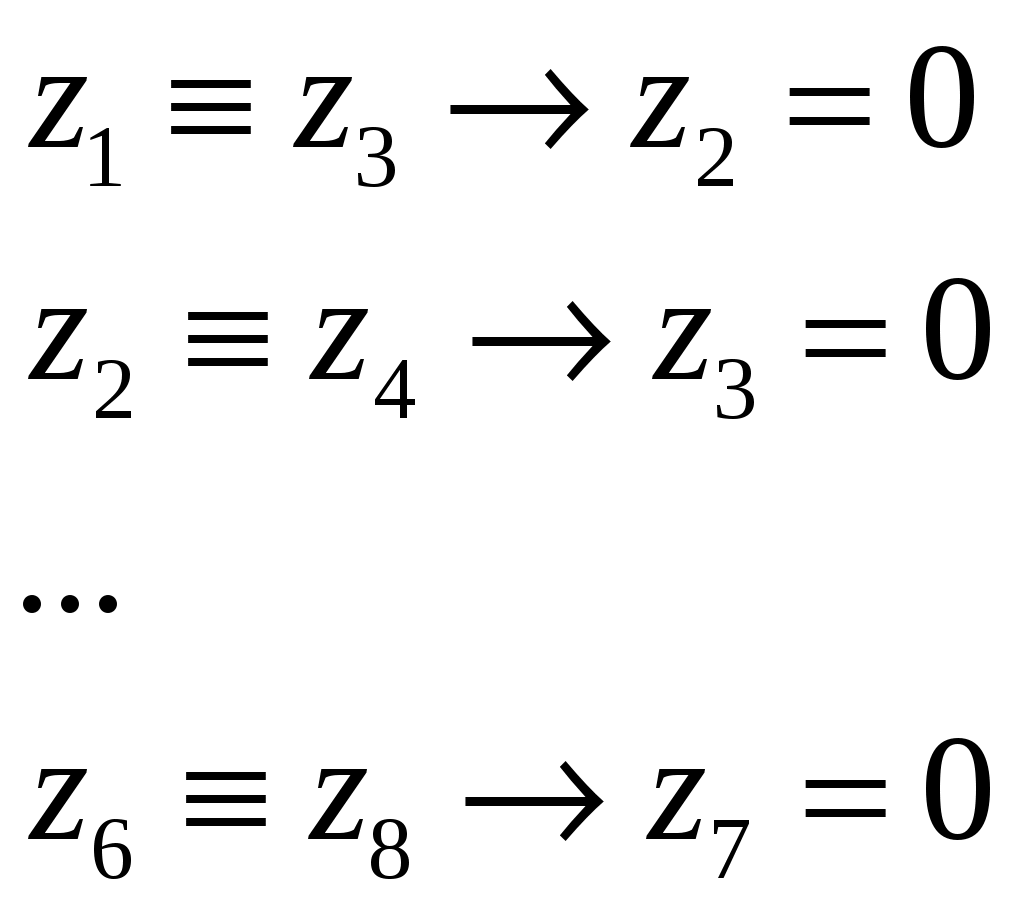



Решим первое уравнение, составив таблицу истинности выражения из левой части

0	0	0	1	0
0	0	1	0	1
0	1	0	1	1
0	1	1	0	1
1	0	0	0	1
1	0	1	1	0
1	1	0	0	1
1	1	1	1	1

Первое уравнение имеет 2 решения (выделены в таблице желтым цветом).

Рассмотрим, что происходит с этими решениями на примере уравнения 2 (переменная во втором уравнении не участвует, но в системе она присутствует, поэтому выделена другим цветом).

0	0	0		1	0
1	0	1			0

Так как правая часть равна 0 (ЛОЖЬ), то получить мы это можем для импликации в единственном случае , т. е для первой строки при известном должно выполняться равенство . Так как значение известно из решения первого уравнения, понятно, что для возможно единственное значение .

Рассмотрим вторую строку. Это импликация , которая должна быть равна 0 (ЛОЖЬ). Но в данном случае это невозможно, так как , значит, при любых значениях выражения импликация будет равна 1 (ИСТИНА).

Значит, система из первых двух уравнений имеет единственное решение.

0	0	0	0

Рассуждая аналогично и анализируя условие системы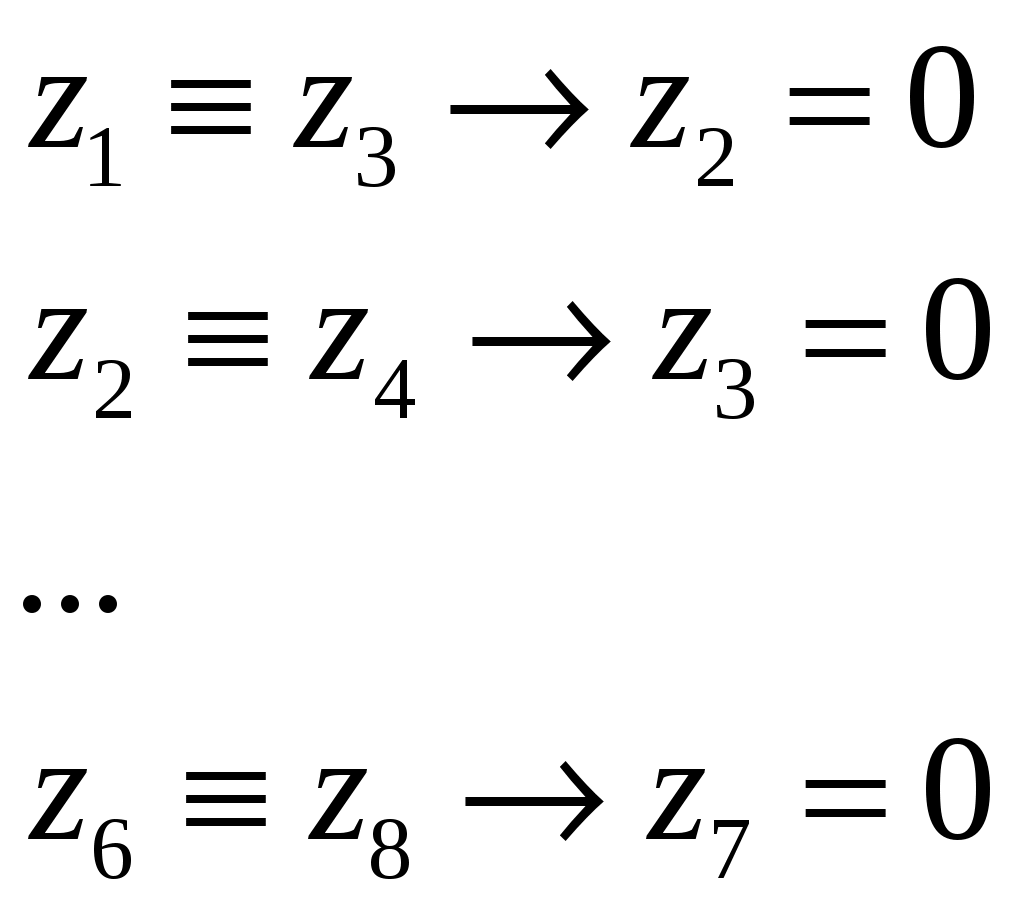

,

получим, что данная система может иметь только единственное решение, в котором значения всех логических переменных равны 0 (ЛОЖЬ):

0	0	0	0	0	0	0	0

Перейдем к исходным обозначениям. Для этого выясним, сколько нулевых и сколько единичных значений дает каждая введенная переменная . Так как переменные однотипны, рассмотрим только первую.

0	0	0
0	1	0
1	0	0
1	1	1

В трех случаях переменная z равна 0, значит, в таблице под каждым решением, где , мы подпишем 3 – такое количество решений в исходных обозначениях даст каждый 0.

0	0	0	0	0	0	0	0
3	3	3	3	3	3	3	3

Теперь, чтобы получить решение исходной задачи, надо перемножить все числа в последней строке:



Различных наборов значений логических переменных , которые удовлетворяют всем перечисленным условиям



существует 6561.
Ответ: 6561