сопромат. Расчетная работа по сопромату 326 вариант. Решение. Число степеней свободы

• Название: Решение. Число степеней свободы
• Анкор: сопромат
• Дата: 12.07.2022
• Размер: 0.73 Mb.
• Имя файла: Расчетная работа по сопромату 326 вариант.doc
• Тип: Решение; #629507

Вариант 326.

Задание 1. Расчет статически определимой многопролетной балки.

Для балки, изображенной на рис.1, требуется построить эпюры поперечной силы Q и изгибающего момента М, линии влияния М и Q для заданного сечения, а также линию влияния одной опорной реакции. Определить по линиям влияния М, Q и R от заданной нагрузки.

Исходные данные:



Рис. 1. Схема многопролетной балки для расчета.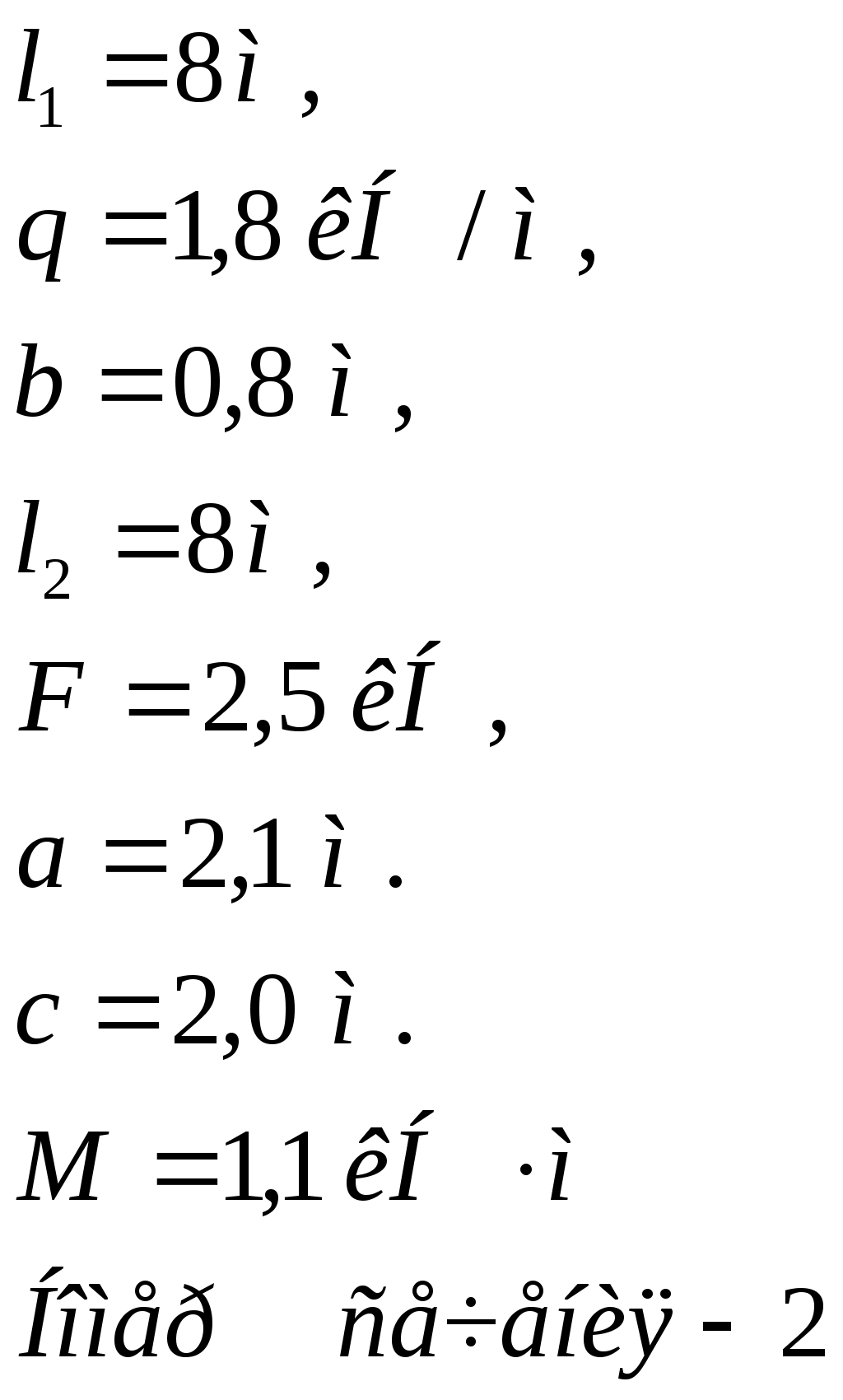



Решение.

1. 
   Число степеней свободы:
   

Поскольку число степеней свободы W = 0, то это значит, что балка статически определима.

2. 
   Составим схему взаимодействия элементов балки (поэтажную схему – рис.2.):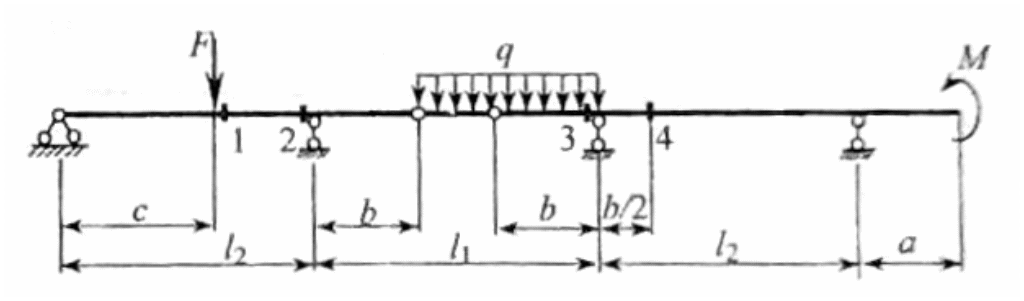
   

Рис. 2. Расчетная схема балки, эпюра поперечных сил Q и изгибающих моментов М.

Расчет балки начнем с «верхнего этажа» - среднего участка балки, нагруженного распределенной силой q.

Заменив распределенную силу эквивалентной сосредоточенной, приложенной в середине участка балки, найдем опорные реакции:



Для определения реакций опор левого пролета балки составим уравнения равновесия:



Отсюда найдем:



Найдем реакцию опоры А: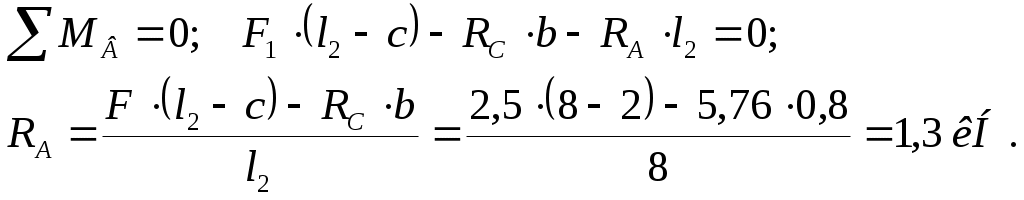



Сделаем проверку расчетов:



Расчет произведен верно.

Для определения реакций опор правого пролета балки составим уравнения равновесия:



Отсюда найдем: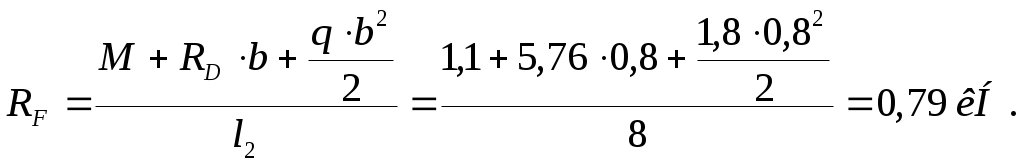



Найдем реакцию опоры E: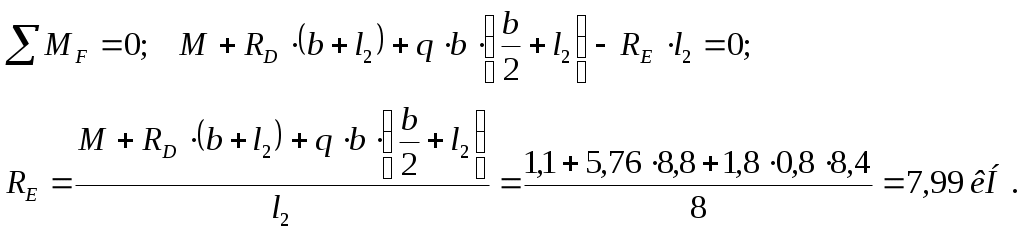



Сделаем проверку расчетов:



Расчеты произведены верно.

Построим эпюру поперечных сил балки.

Разобьем балку на 6 участков (отмечены римскими цифрами на рис.2), рассчитаем поперечную силу на каждом из участков.

Для участка I:



Для участка II:



Для участка III:



Для участка IV:







Для участка V:



Для участка VI:



Строим эпюру крутящих моментов М.







Для участка балки CD:

На концах участка: M_C = M_D­ = 0 кН∙м,

В центре участка:






Строим линии влияния для сечения 2.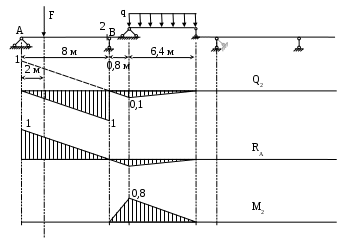



Рис. 3. Линии влияния от опоры A, а также линии влияния М и Q для сечения 2.
Рассчитаем усилие в сечении 2 от сил, действующих на балку:



Результаты расчета по линиям влияния и стандартным методом совпали, следовательно, расчеты выполнены верно.
Задание 4. Определение перемещений в статически определимых рамах.

Исходные данные.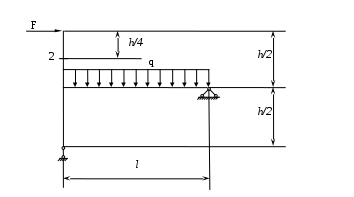





Рис. 4. Исходные данные к задаче№4.

1. 
   Определим реакции опор. Для этого мысленно отбросим опоры рамы, заменив их реакциями (рис. 5.)
   

Из уравнения равновесия по оси Х:



Рассмотрим равновесие системы относительно опоры А: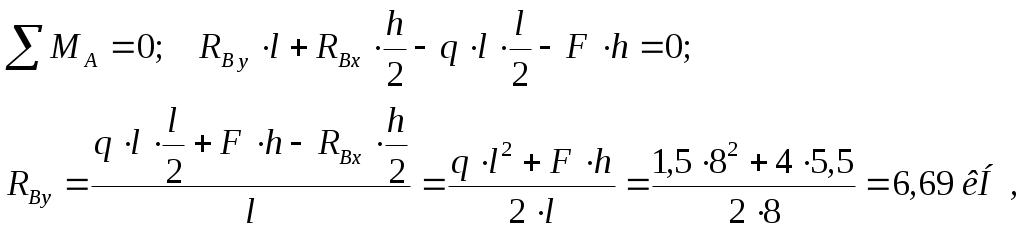



Рассмотрим равновесие системы относительно опоры В: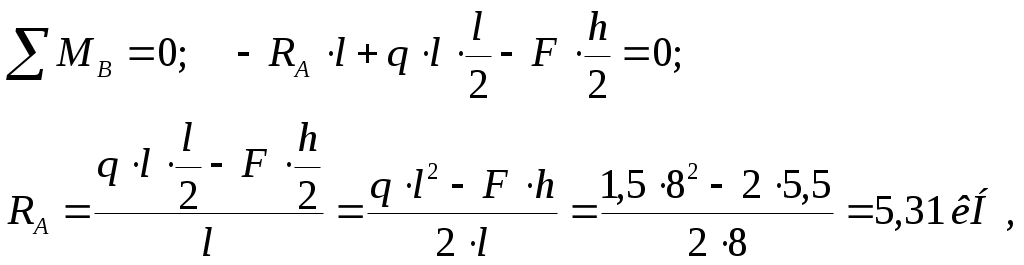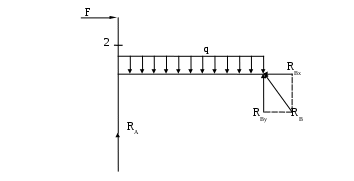



`

Рис. 5. К определению реакций опор.

Сделаем проверку:



Расчет выполнен верно.

Нанесем на схему рамы грузовую эпюру моментов (рис. 6)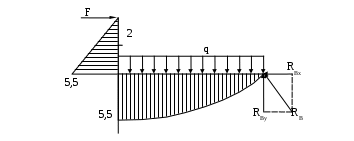



Рис. 6. Грузовая эпюра рамы.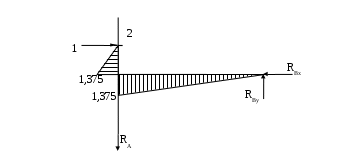



Рис. 6. Эпюра от единичной нагрузки.

Для определения перемещения сечения 2 воспользуемся правилом Верещагина: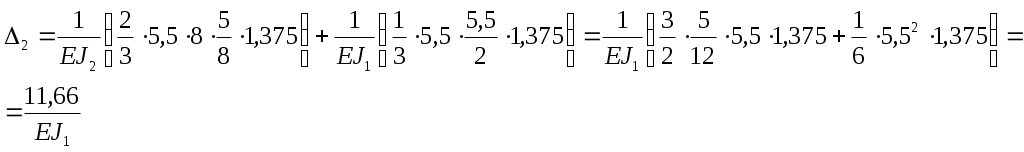



Ответ: сечение 2 сместится на

Задание №5. Расчет плоской статически неопределимой рамы методом сил.

Для рамы (рис. 7) требуется:

- построить эпюры изгибающих моментов, поперечных и продольных сил;

- проверить правильность построенных эпюр.



Рис. 7. Схема рамы.

Исходные данные: q₁ = 0; q₂ = 0; q₃ = 2 кН/м; F₁ = 0; F₂=0; F₃ = 5 кН; h=8м,
l = 9м.

1. 
   Определим число статической неопределимости:
   

Система дважды статически неопределима.

2. 
   Составим симметричную основную систему с группировкой неизвестных (рис. 8).
   

Неизвестное X₁ – симметричное, а неизвестное X₂ – обратносимметричное.

3. 
   Система канонических уравнений для определения двух неизвестных в общем случае запишется в виде: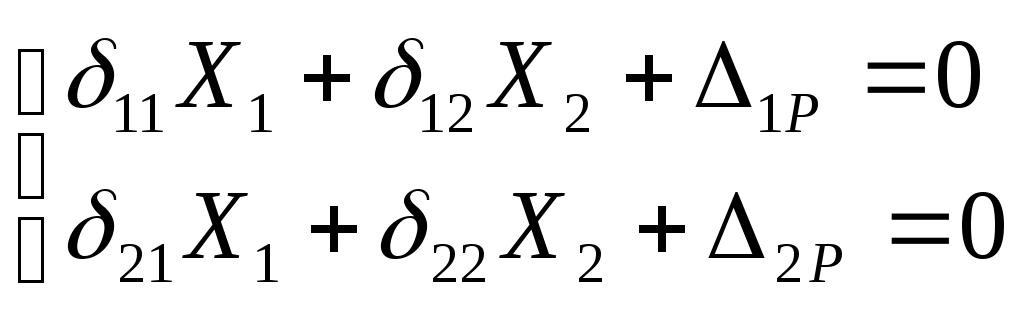
   

4. 
   Последовательно загружая основную систему силами Х₁ = 1,
   Х₂ = 1, и внешней силовой нагрузкой, строим единичные эпюры М₁, М₂, грузовую эпюру М_Р, а также суммарную единичную эпюру М_S ( соответственно рис. 9,10,11,12).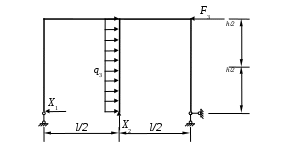
   

Рис. 8. Основная система.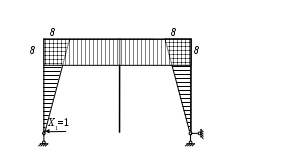



Рис. 9. M₁.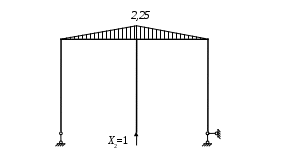



Рис. 10. M₂.



Рис. 11. Грузовая эпюра.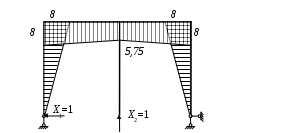



Рис. 12. M_S.

5. 
   Вычисляем коэффициенты при неизвестных, свободные члены и производим проверку.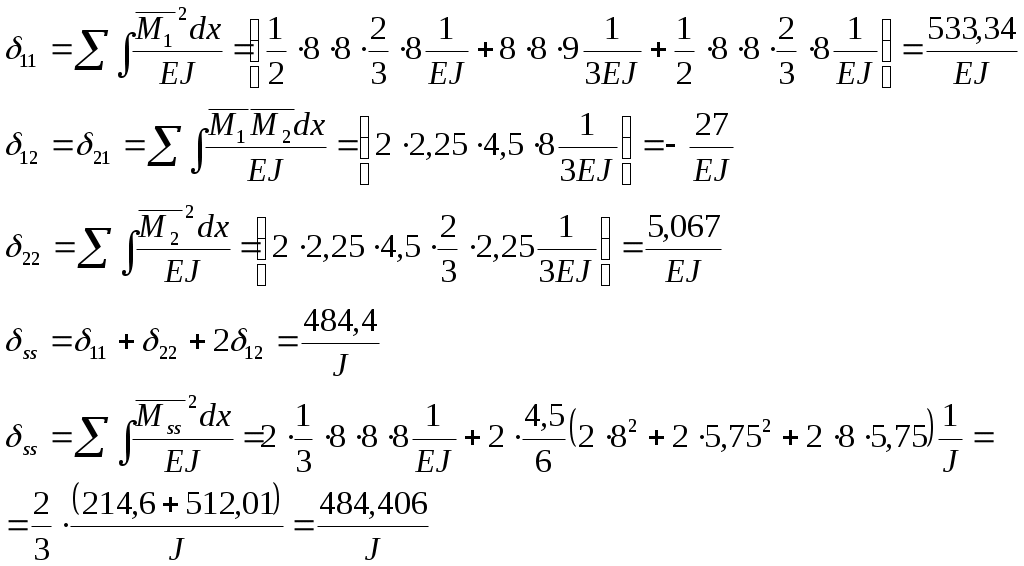
   

Ошибка составляет: 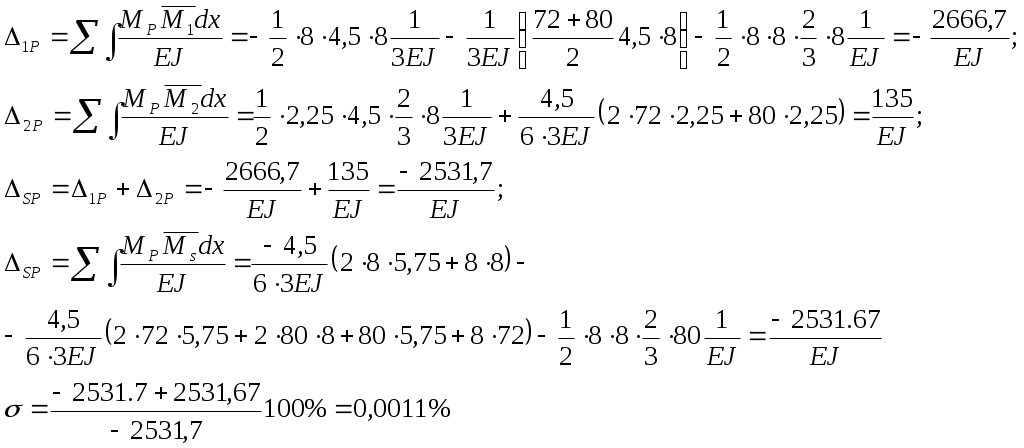, то есть коэффициенты найдены верно.



Коэффициенты найдены верно.

6. 
   Подставим найденные коэффициенты в систему уравнений и решим ее: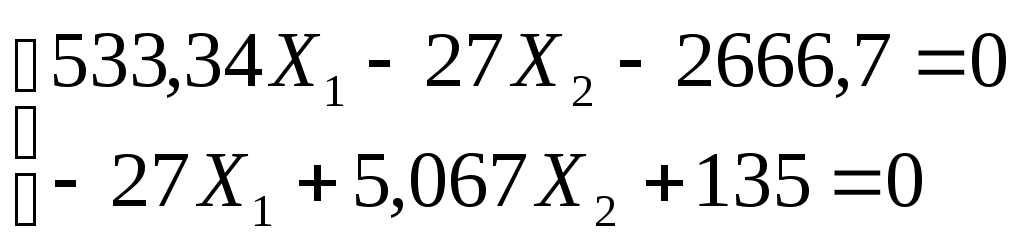
   

Находим:

7. 
   Строим исправленную эпюру М₁Х₁, и окончательную эпюру М (эпюру М₂Х₂ строить не надо, так как Х₂ = 0).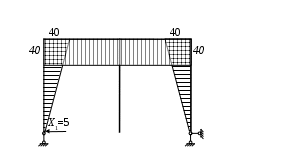
   

Рис. 13. Исправленная эпюра М₁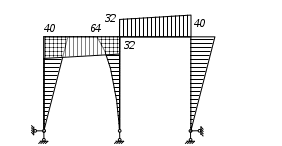



Рис. 14. Окончательная эпюра М.

8. 
   Произведем кинематическую проверку.
   

Следовательно, эпюра моментов построена верно.

9. 
   Строим эпюру поперечных сил.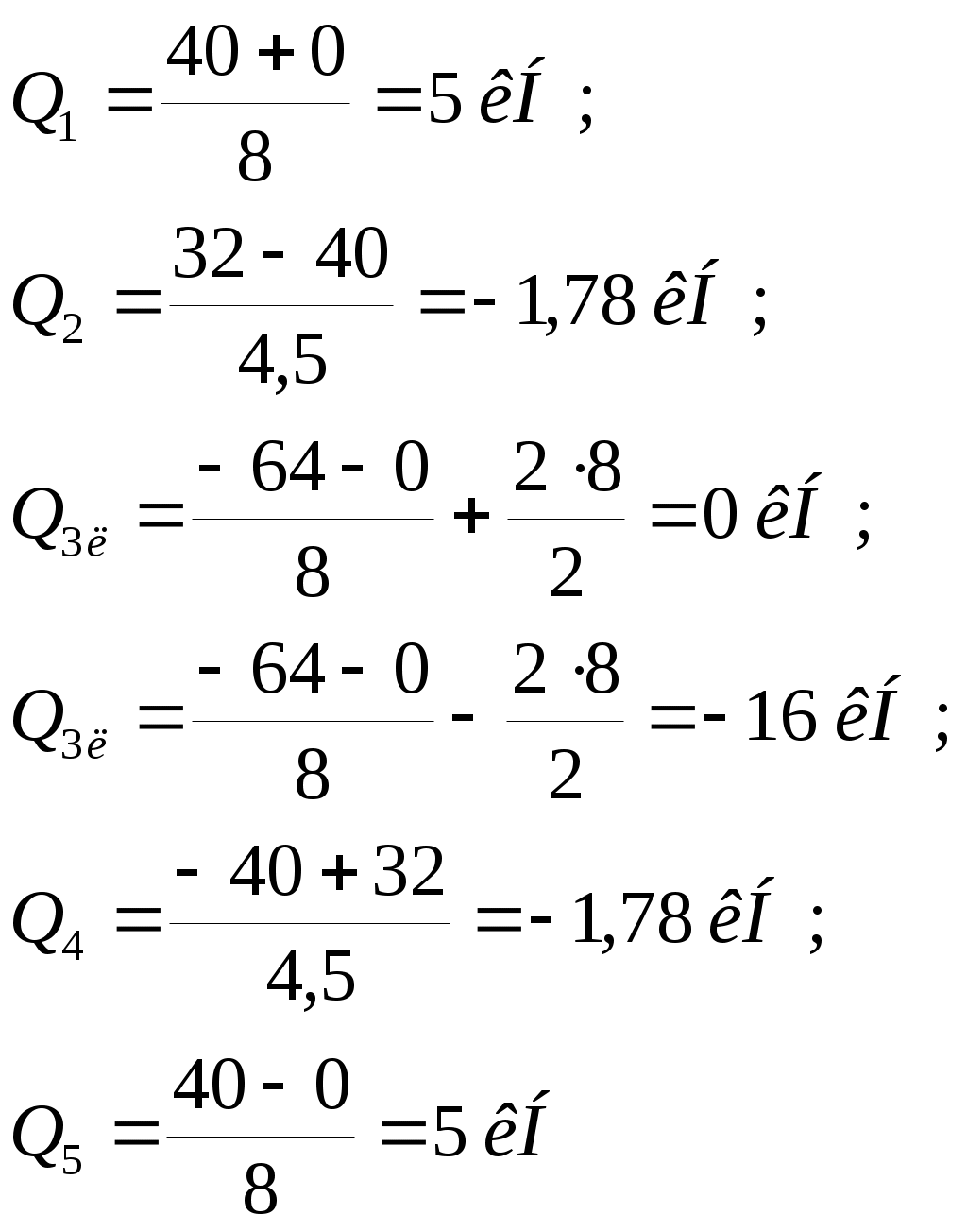
   

Рис. 15. Эпюра Q.

10. 
    По полученной эпюре Q строим эпюру N.
    

Рис. 16. Эпюра N.

11. 
    По полученным эпюрам строим раму с отброшенными связями и приложенными взамен них силами, чтобы провести статическую проверку рамы (рис. 17).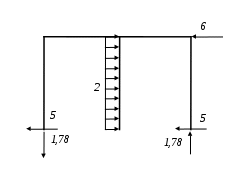
    

Рис. 17. Рама с отброшенными связями для статической проверки.

Запишем уравнения равновесия:



Следовательно, эпюры построены правильно.

Задание 9. Расчет рам на динамическое воздействие.

Для рамы (рис. 18) требуется:

- определить частоты собственных колебаний , приняв раму как систему с двумя степенями свободы (собственный вес не учитывается).

- построить эпюру моментов от заданного динамического воздействия, приняв частоту возмущающей силы .

Исходные данные: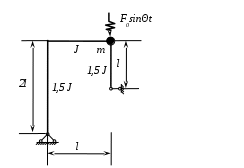



Рис. 18. Рама для динамического расчета.

1. 
   Запишем вековое уравнение для системы с двумя степенями свободы:
   

Здесь частота свободных колебаний, .

Для нашего слу­чая m₁ = m₂ = m.

2. 
   Строим единичные эпюры от единичных сил инерции, приложенных в направлении возможных колебаний (рис. 19,20).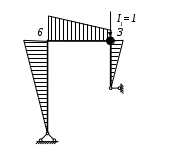
   

Рис. 19. Эпюра моментов от единичной силы I₁ = 1.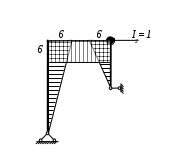



Рис. 20. Эпюра моментов от единичной силы инерции I₂ = 1.

3. 
   Найдем коэффициенты векового уравнения: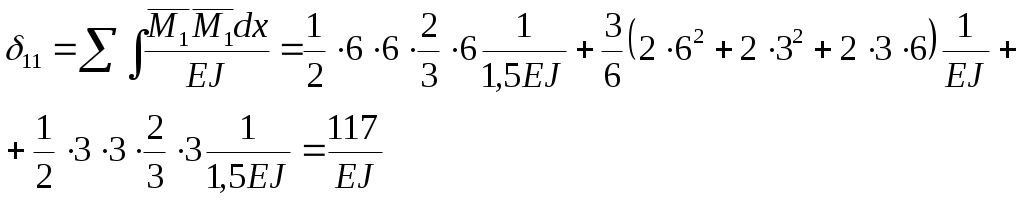
   

Подставляем полученные коэффициенты в вековое уравнение.

4. 
   Вычисляем значения частот свободных колебаний:
   

отсюда



решая уравнение относительно λ, получим: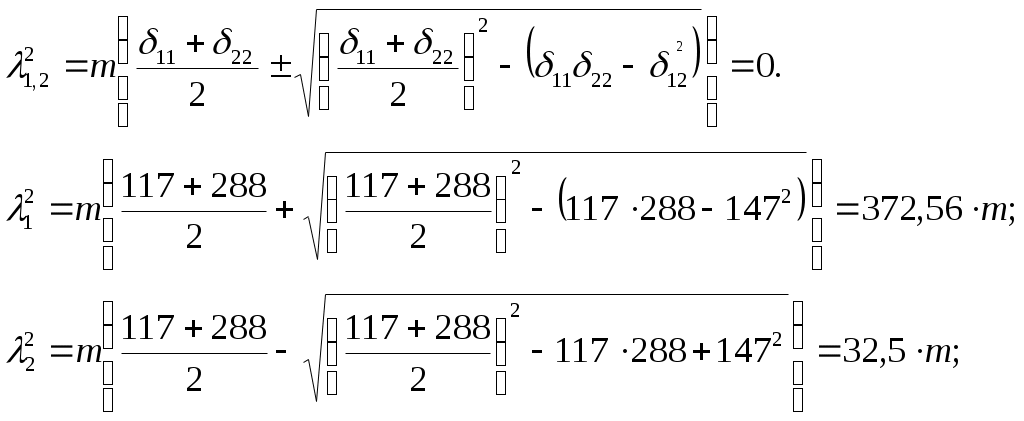



;

,

5. 
   Построим эпюру моментов в заданной раме от амплитудного значения вибрационной нагрузки.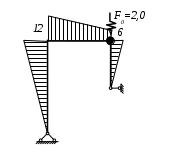
   

Рис. 21. Эпюра М_F0.

6. 
   Найдем амплитудные значения сил инерции, решив систему уравнений:
   

Здесь 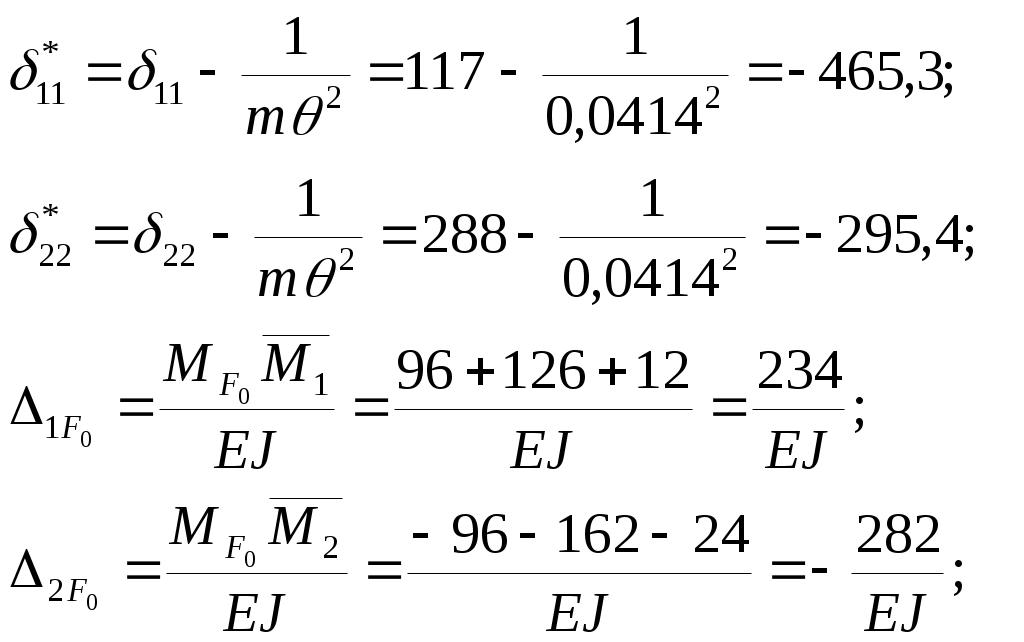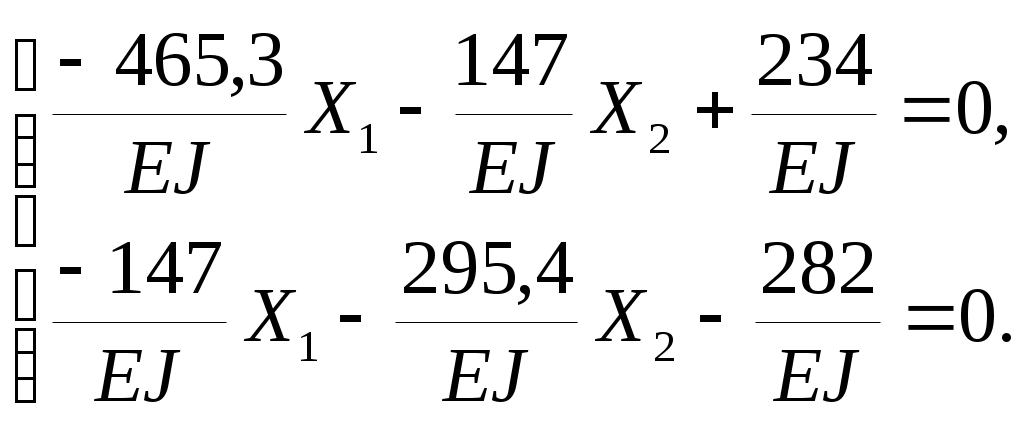перемещение точки приложения массы в i-m направлении возможных колебаний от амплитудного значения вибрационной нагрузки.





Отсюда найдем:

7. 
   Исправим эпюры моментов от единичных сил инерции (рис. 22, 23).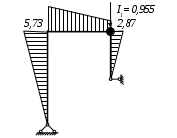
   

Рис. 22. Исправленная эпюра от силы инерции I₁.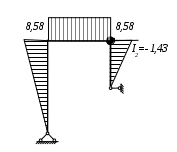



Рис. 23. Исправленная эпюра от силы инерции I₂.

8. 
   Построим эпюру моментов от динамической нагрузки как суммарную эпюру от статически приложенных амплитудных значений сил инерции и вибрационной нагрузки (рис. 24).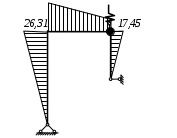
   

Рис. 24. Эпюра моментов от динамической нагрузки.