сопротивления матер. 3ГД-У. Сопротивление материалов
 Скачать 2.48 Mb. Скачать 2.48 Mb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный университет геосистем и технологий» (СГУГиТ) Кафедра специальных устройств и технологий СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ Вариант №3 Выполнил: Проверил: студент группы 3ГД-У д.т.н., профессор . Савелькаев С.В. Новосибирск СГУГиТ 2022 Вариант 3. Задание 1. Определение реакций опор и реакции связи плоской составной конструкции. Исходные данные: 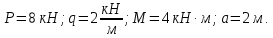 Схема задания: 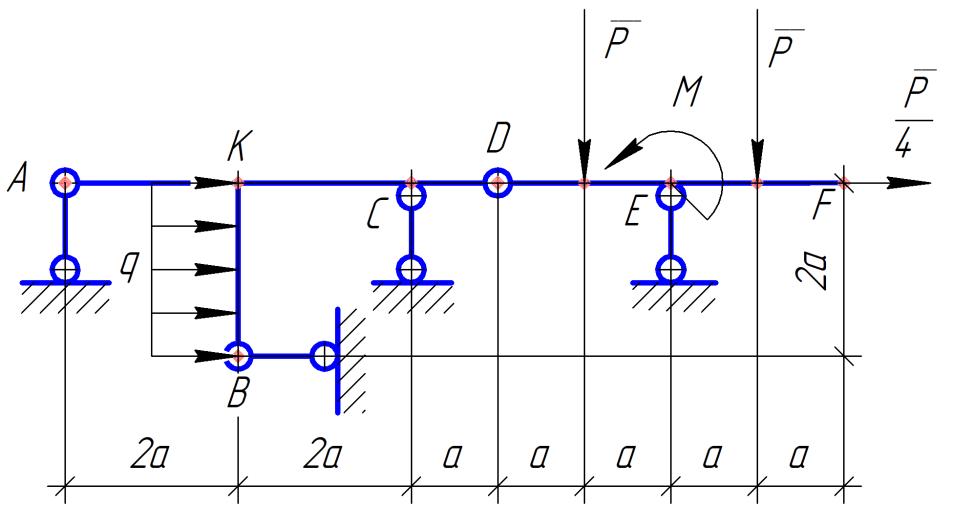 Определить реакции опор  и реакции в шарнире и реакции в шарнире  Решение. 1. Рассмотрим составную балку 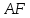 по частям: по частям: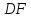 и и 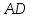 . .Начнем с правой части 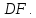 Отбрасываем связь и опору, заменяя их действие реакциями: 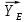 – каток в т. – каток в т.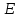 , , 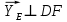 ; ;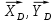 - реакции в шарнире в т. - реакции в шарнире в т.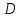 , действующие на балку , действующие на балку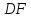 со стороны балки со стороны балки 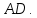 Получили расчетную схему для балки 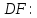 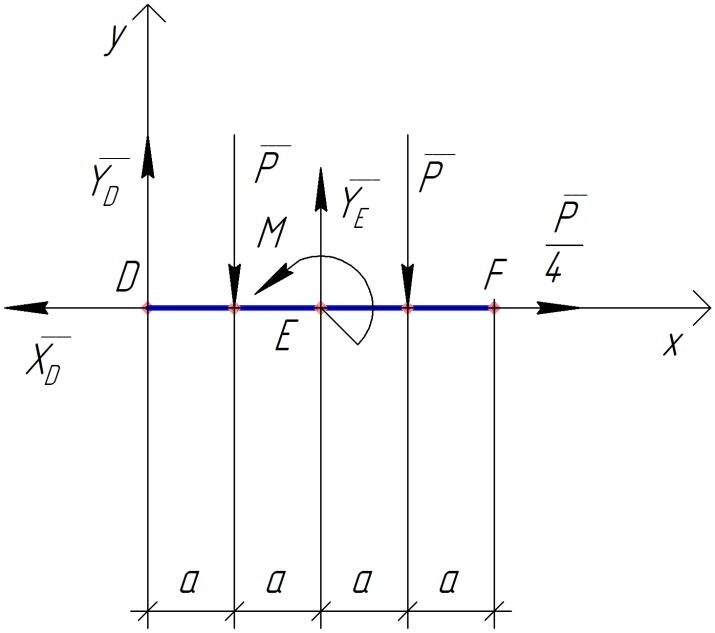 2. Для произвольной плоской системы сил составляем 3 уравнения равновесия: 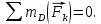 (1) (1)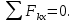 (2) (2)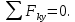 (3) (3) Из (1): 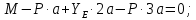 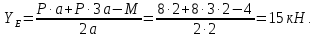 Из (2): 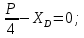 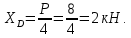 Из (3): 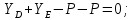 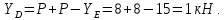 3. Теперь рассмотрим балку AD. Также отбрасываем опоры и связи, заменяя их действие реакциями:  - катки в точках - катки в точках  соответственно; соответственно;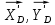 - реакции в шарнире в т. - реакции в шарнире в т.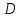 , действующие на балку AD со стороны балки , действующие на балку AD со стороны балки 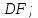 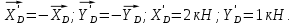 Распределенную нагрузку 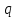 заменяем сосредоточенной силой заменяем сосредоточенной силой 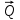 , приложенной в т. , приложенной в т.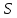 - середине участка - середине участка 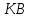 ; ; 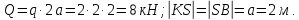 Получили расчетную схему балки AD:  4. Также составляем 3 уравнения равновесия:  (4) (4) (5) (5)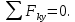 (6) (6) Из (4): 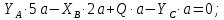 (7) (7)Из (5): 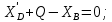 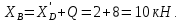 (8) (8)Из (6): 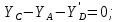 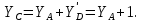 (9) (9)Подставляем (9) и (8) в (7): 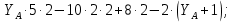 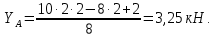 Находим: 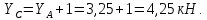 5.Определили реакции опор и связи. Для проверки рассмотрим всю балку целиком и составим уравнение равновесия: 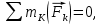 (достаточно одного уравнения); (достаточно одного уравнения);Получили расчетную схему для всей балки: 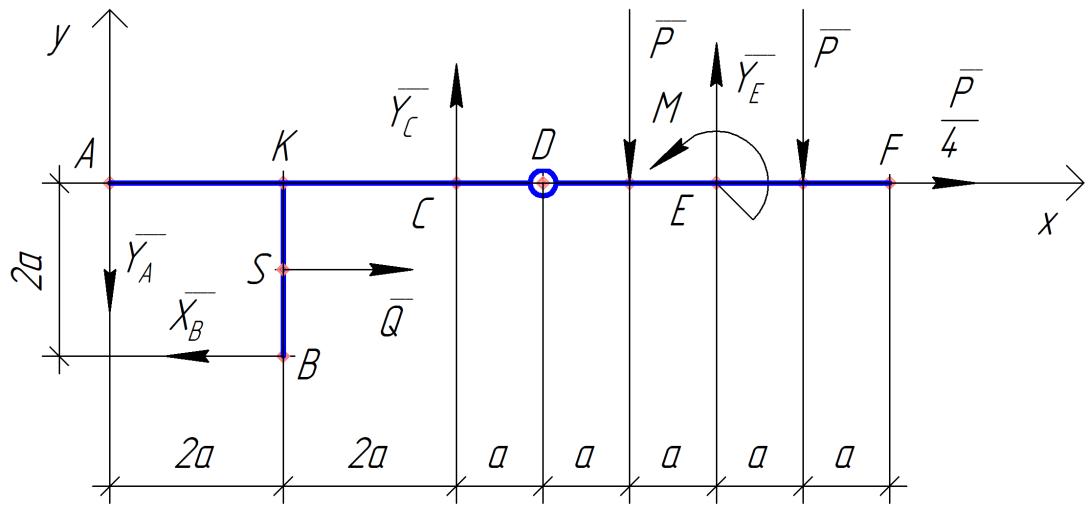 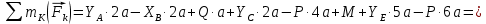 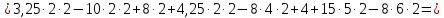  Следовательно, реакции определены верно. Направления реакций опор совпадают с направлениями, указанными на расчетной схеме балки целиком. 6. В заключении, определим абсолютную величину реакции в шарнире 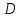 : :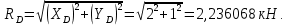 Ответ: 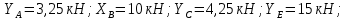 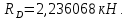 Задание 2. Определение реакций опор пространственной конструкции. Исходные данные: 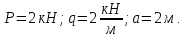 Схема задания: 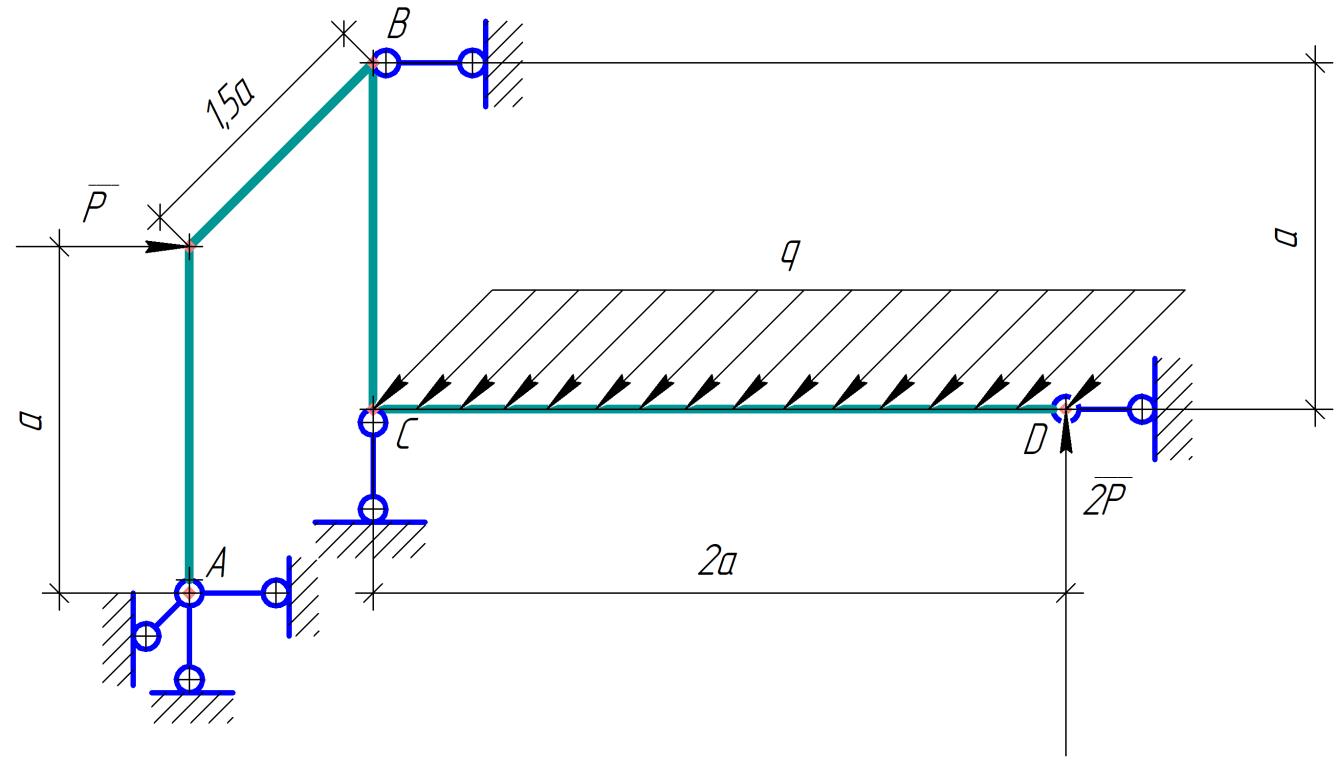 Определить реакции опор в точках 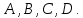 Решение. 1.Вводим систему координат 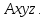 Отрбрасываем связи (опоры), заменяя их действие реакциями: Отрбрасываем связи (опоры), заменяя их действие реакциями: – в точке – в точке 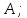 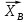 – в точке – в точке 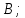 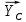 - в точке - в точке 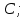 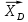 - в точке - в точке 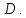 Распределенную нагрузку 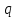 заменяем сосредоточенной силой заменяем сосредоточенной силой 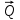 , приложенной в т. , приложенной в т.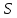 - середине участка - середине участка 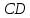 ; ; 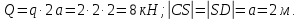 Получили расчетную схему конструкции: 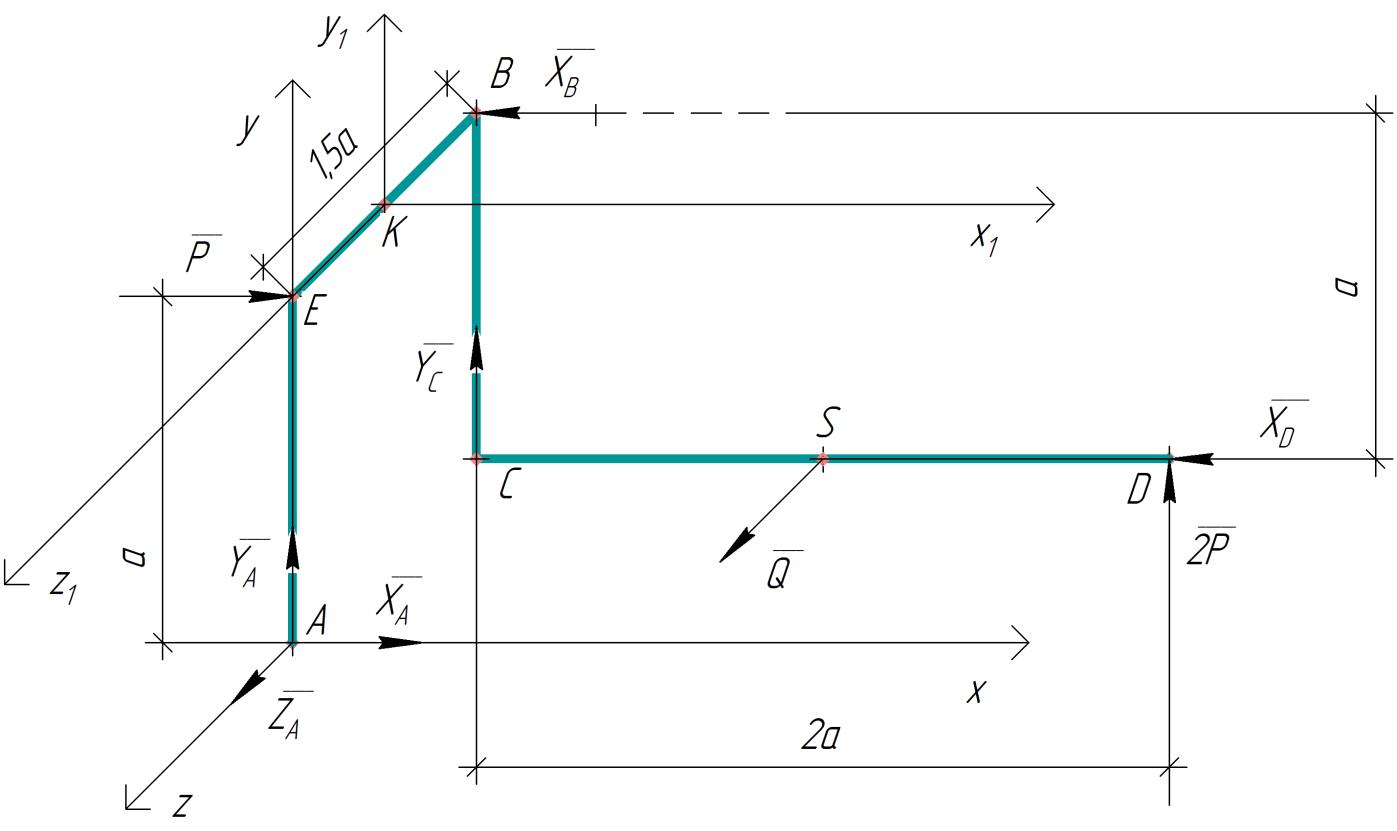 2. У нас имеется 6 неизвестных реакций опор. Для произвольной пространственной системы сил можем составить 6 уравнений равновесия. Следовательно, конструкция статически определима. 3.Составляем уравнения равновесия: 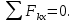 (1) (1)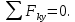 (2) (2)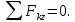 (3) (3) 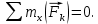 (4) (4) 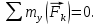 (5) (5) 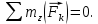 (6) (6)4. Находим: Из (4): 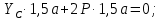 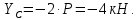 Из (6): 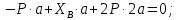 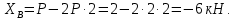 Из (5): 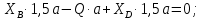 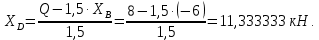 Из (1): 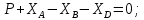 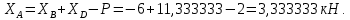 Из (2): 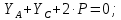 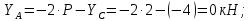 Из (3): 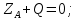 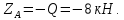 Знаки «  » перед » перед  говорит о том, что направления говорит о том, что направления 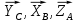 противоположны направлениям, указанным на расчетной схеме. противоположны направлениям, указанным на расчетной схеме.5. Для проверки составим уравнения моментов сил относительно осей 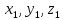 ? параллельных осям ? параллельных осям 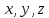 соответственно и проходящим через т. соответственно и проходящим через т.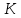 - середину участка - середину участка 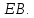 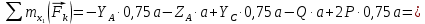 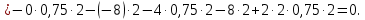 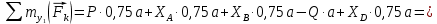 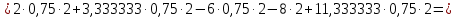 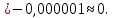 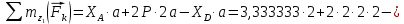 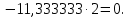 Следовательно, реакции опор определены верно. В заключении найдем абсолютную величину реакции в точке 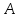 : :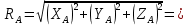 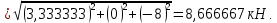 Ответ: 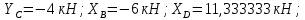 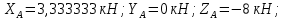 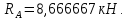 Задание 3. Определение продольных сил, нормальных напряжений и перемещений при осевом растяжении и сжатии стержня. Расчет стержня на прочность. Исходные данные: 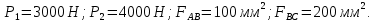 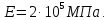 Схема задания: 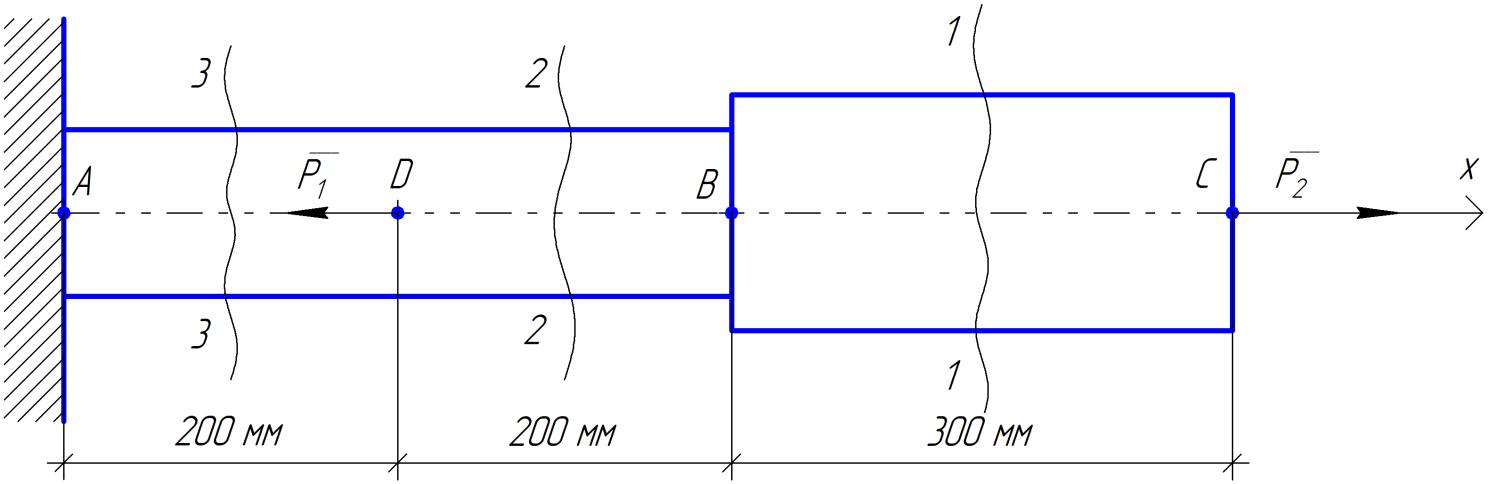 Требуется: -построить эпюры внутренних продольных сил 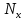 , нормальных напряжений , нормальных напряжений 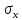 и перемещений и перемещений 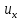 поперечных сечений стержня; поперечных сечений стержня;-проверить перемещение свободного конца, используя принцип независимости действия сил; -проверить стержень на прочность, полагая, что стержень изготовлен из хрупкого материала с пределом прочности при растяжении 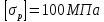 и сжатии и сжатии 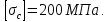 . .Решение. 1. Разбиваем стержень на участки 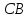 , ,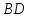 и и 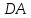 . Используя метод сечений, определяем продольные усилия . Используя метод сечений, определяем продольные усилия 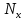 и нормальные напряжения и нормальные напряжения 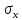 на каждом участке, начиная с консольного (не закрепленного конца стержня) и рассматривая равновесие правой отсеченной части. При этом растягивающие (от сечения) усилия считаем положительными, сжимающие – отрицательными. Сечения на участках обозначены 1-1, 2-2 и 3-3. на каждом участке, начиная с консольного (не закрепленного конца стержня) и рассматривая равновесие правой отсеченной части. При этом растягивающие (от сечения) усилия считаем положительными, сжимающие – отрицательными. Сечения на участках обозначены 1-1, 2-2 и 3-3.Участок 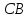 (сечение 1-1). (сечение 1-1).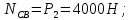 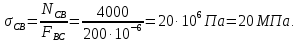 Участок 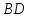 (сечение 2-2). (сечение 2-2).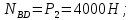 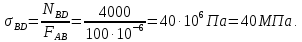 Участок  (сечение 3-3). (сечение 3-3).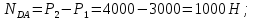 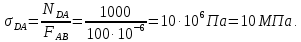 Как видим, на всех участках стержень растянут, следовательно, произошла деформация растяжения(+). По полученным данным строим эпюру продольных сил 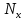 и эпюру нормальных напряжений и эпюру нормальных напряжений 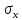 в масштабе. Принимаем масштабные коэффициенты: в масштабе. Принимаем масштабные коэффициенты: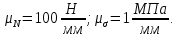 2. Построим эпюру перемещений поперечных сечений стержня 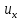 , используя для каждого участка развернутый закон Гука для определения деформаций (в нашем случае удлинения) каждого участка: , используя для каждого участка развернутый закон Гука для определения деформаций (в нашем случае удлинения) каждого участка: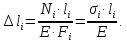 Поперечные сечения проведем через характерные точки:A,D,B,C.  сечение в т. сечение в т. – неподвижно. – неподвижно.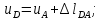 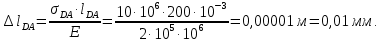 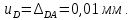 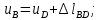 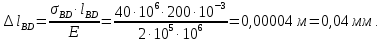 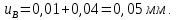 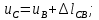 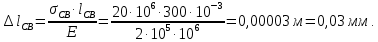 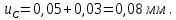 3. Полное удлинение стержня: 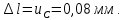 Проверим смещение точки 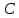 стержня по принципу независимости действия сил. Рассчитаем стержня по принципу независимости действия сил. Рассчитаем 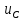 от действия сил от действия сил 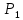 и и 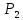 отдельно: отдельно: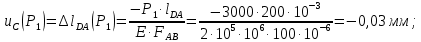 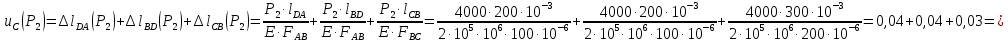 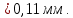 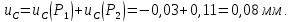 Как видим, перемещение точки  определено верно. определено верно.Строим эпюру перемещений поперечных сечений стержня 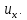 Принимаем масштабный коэффициент: 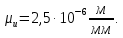 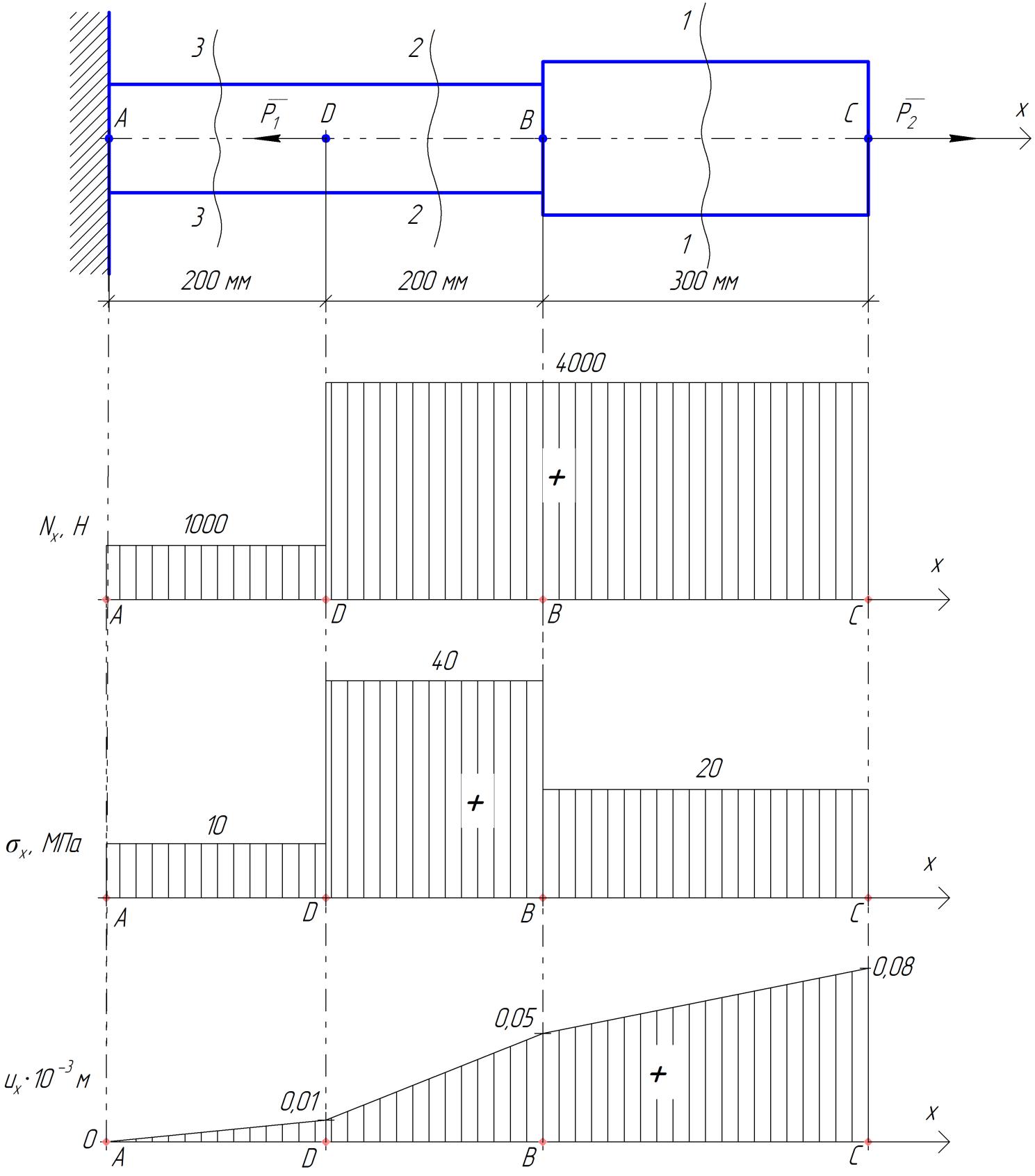 4. Проверим стержень на прочность. Так как, стержень у нас подвергается только деформации растяжения, то используем условие прочности при растяжении(+): 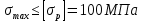 ; ; 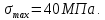 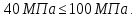 Условие прочности выполняется при заданных нагрузках, геометрических характеристиках и свойствах материала стержня. Коэффициент запаса по пределу прочности: 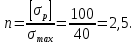 |
