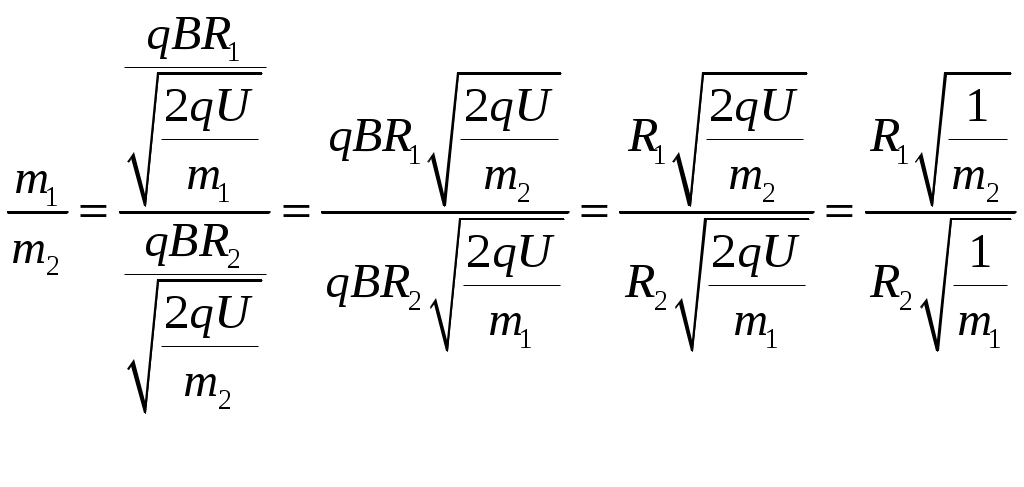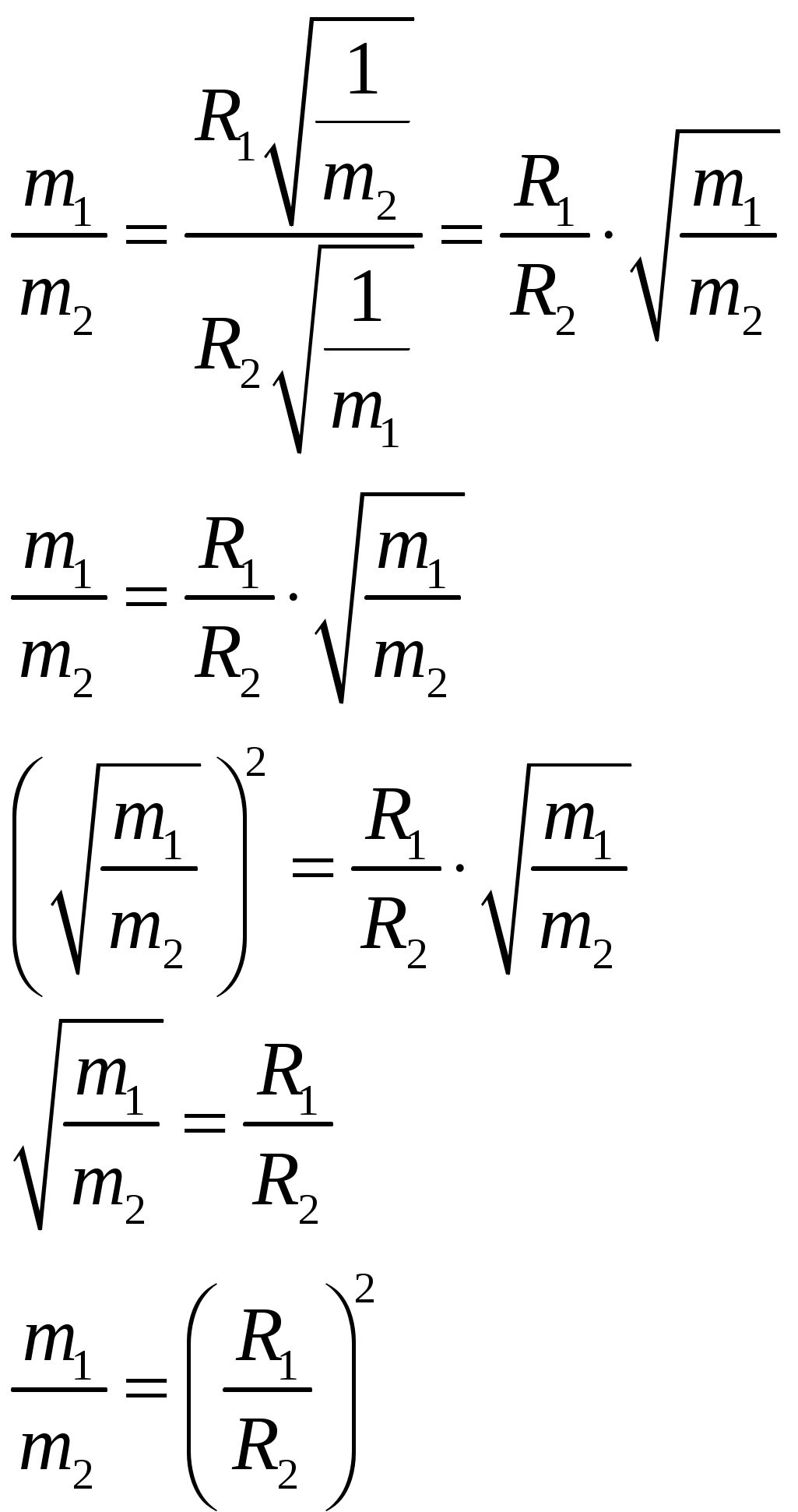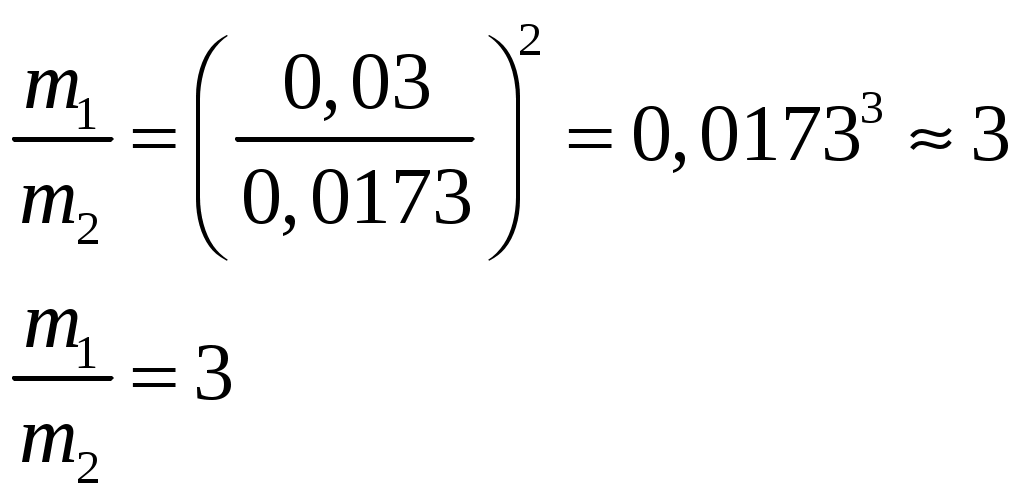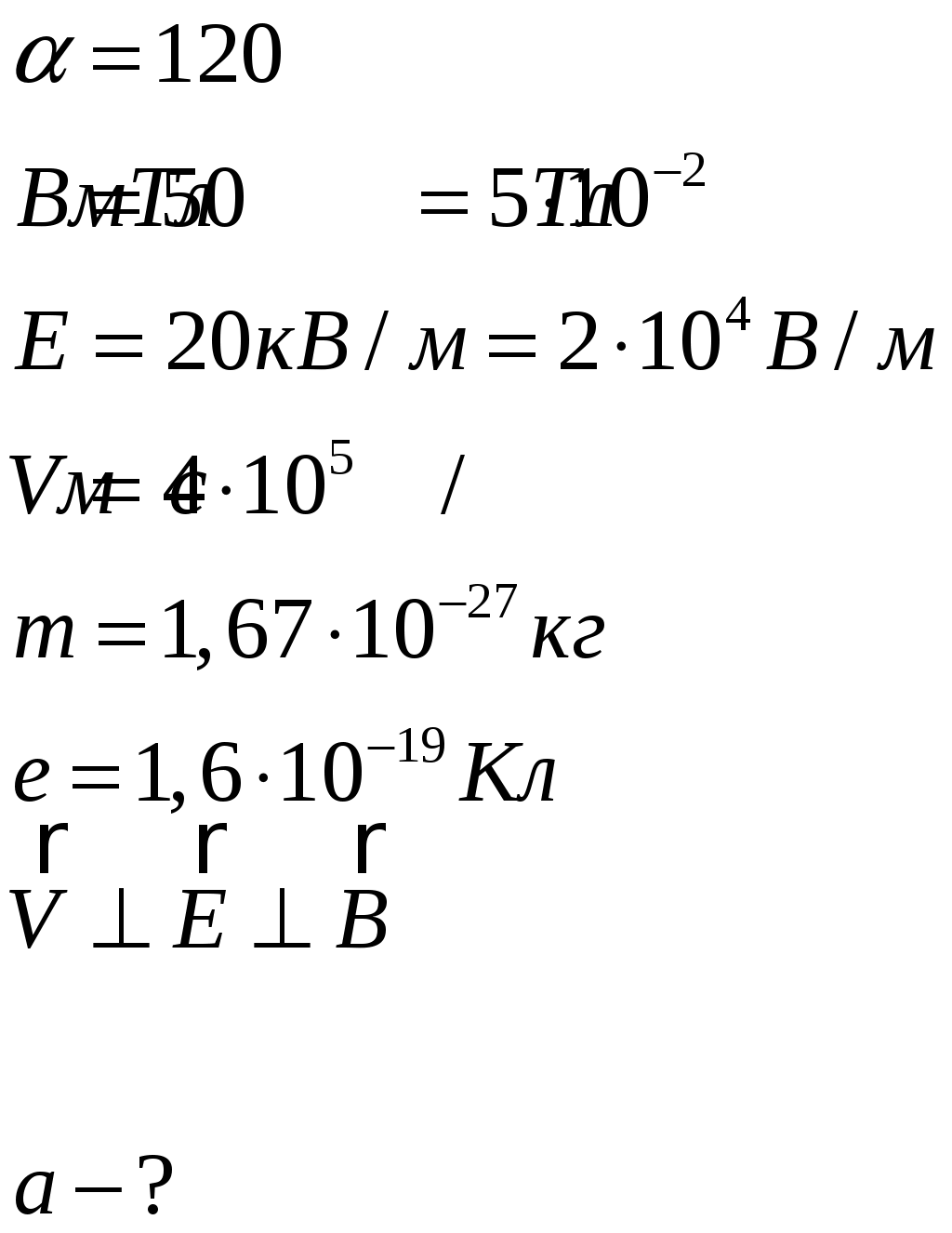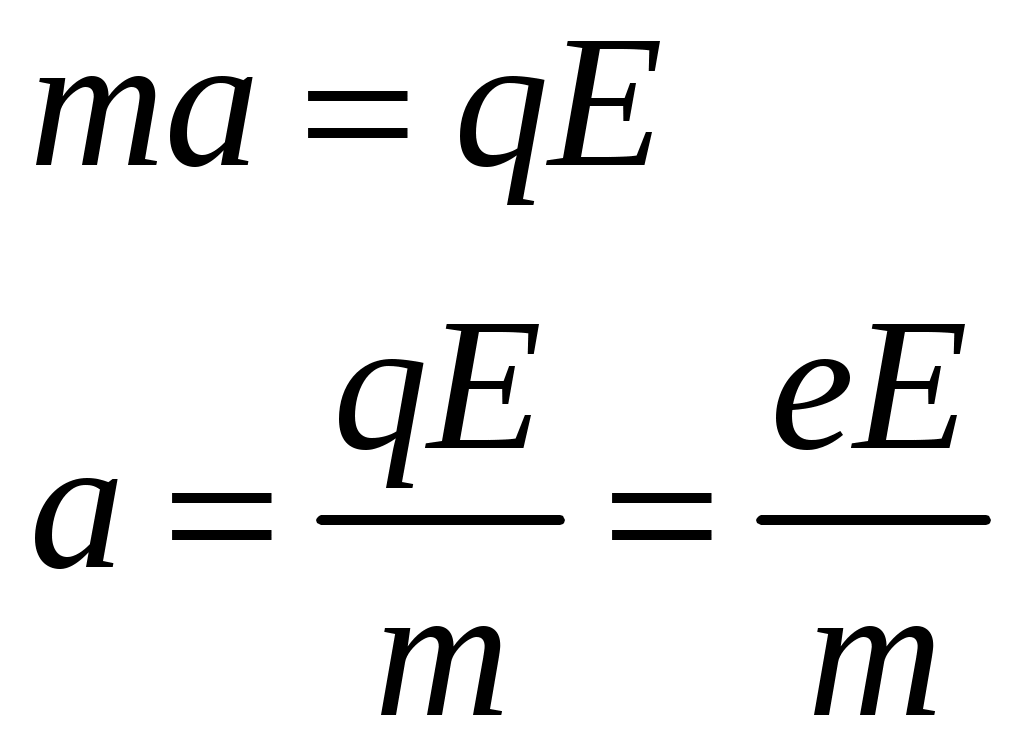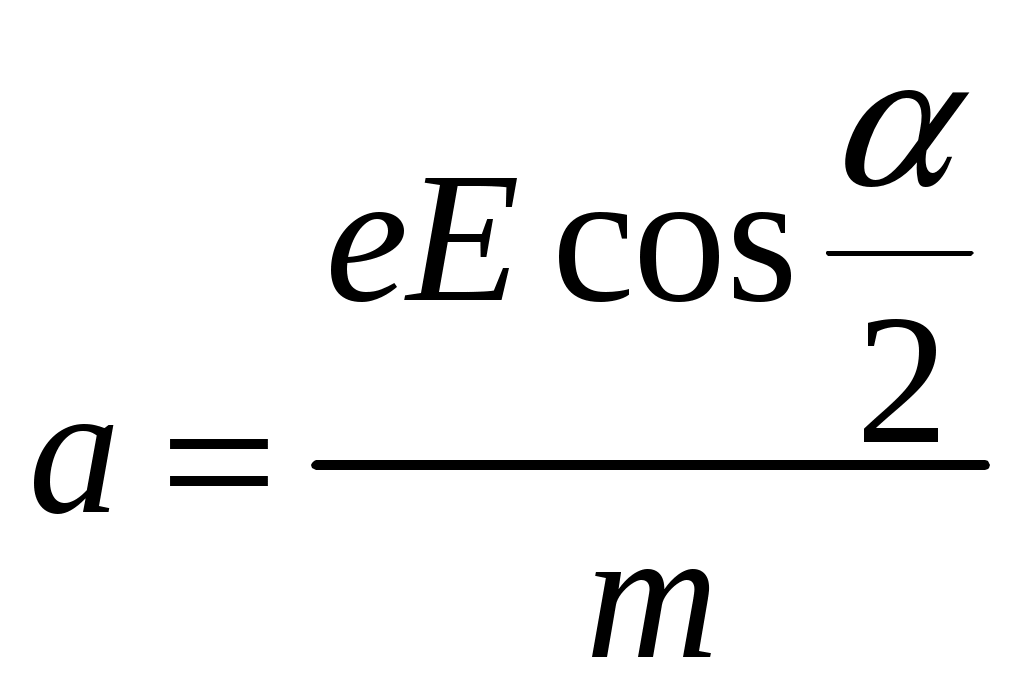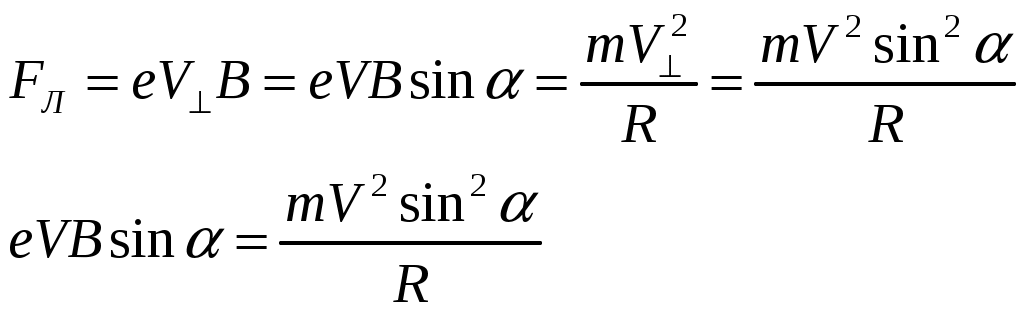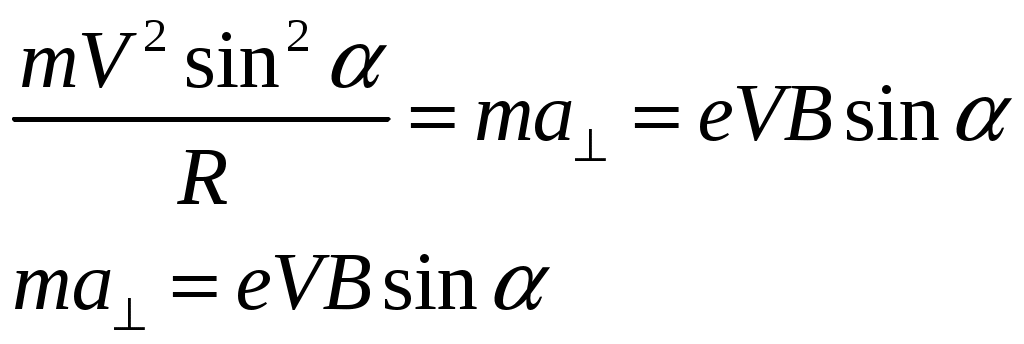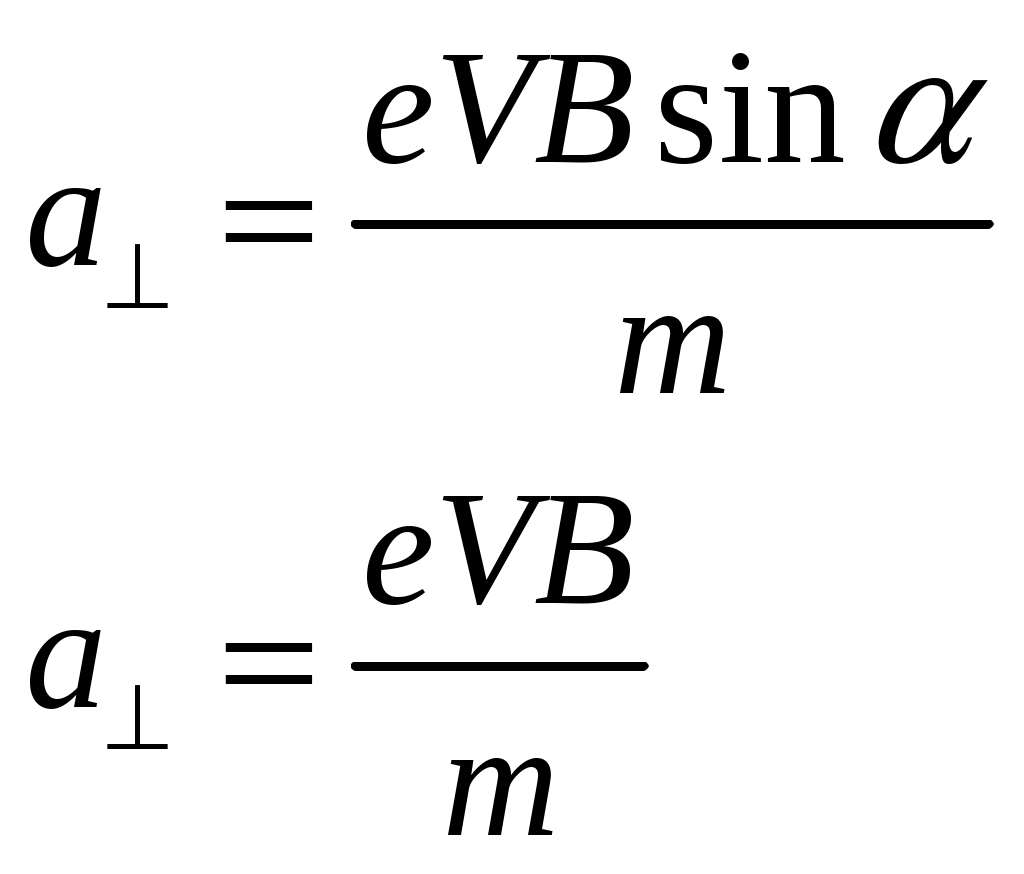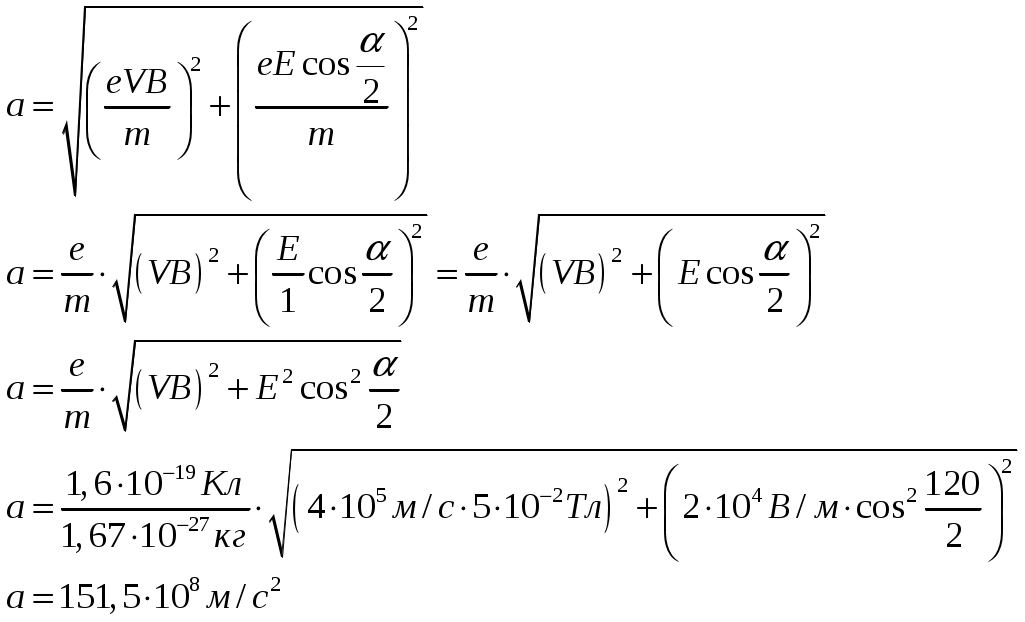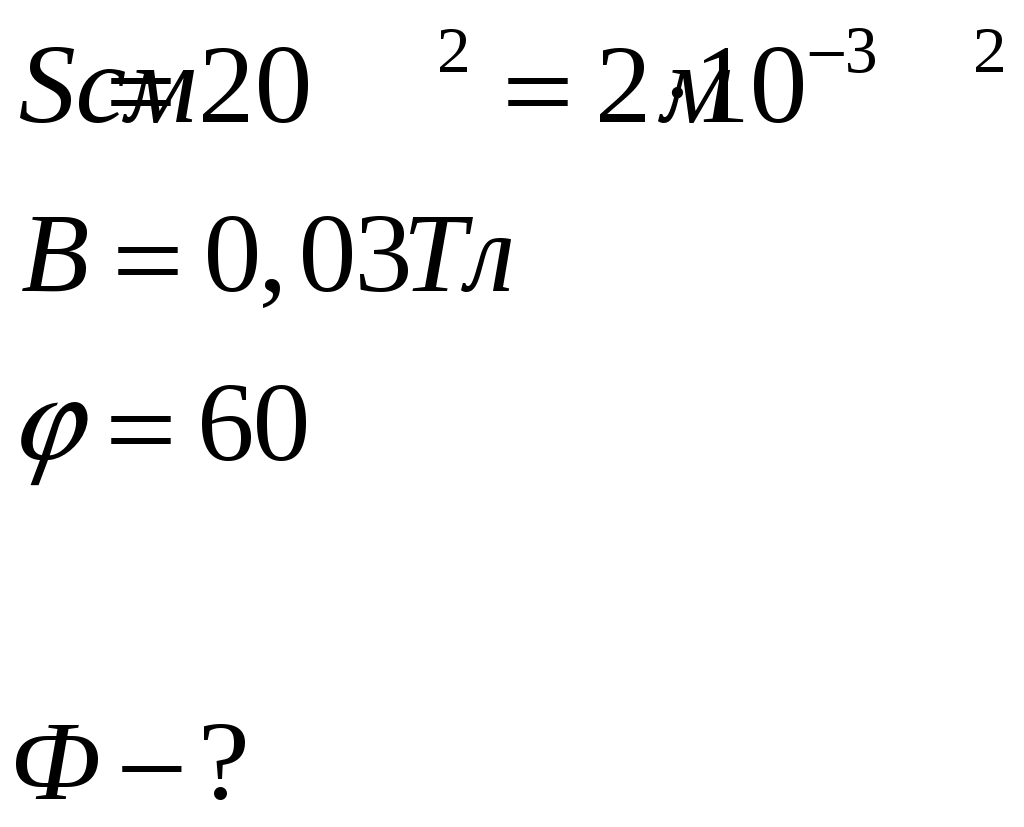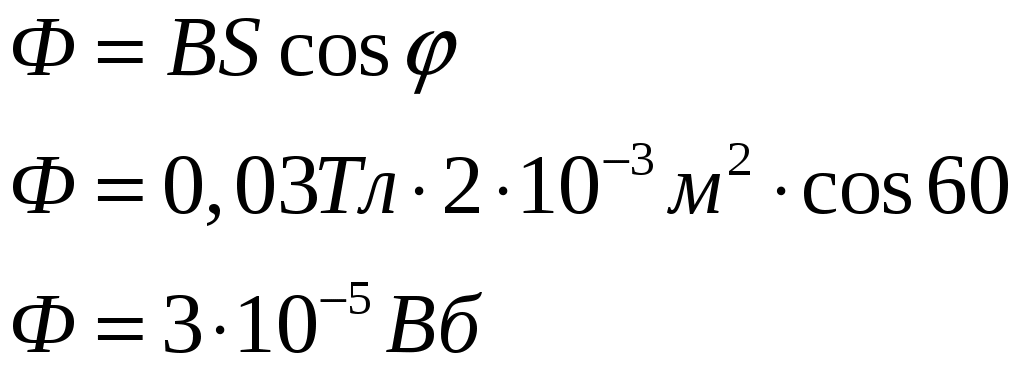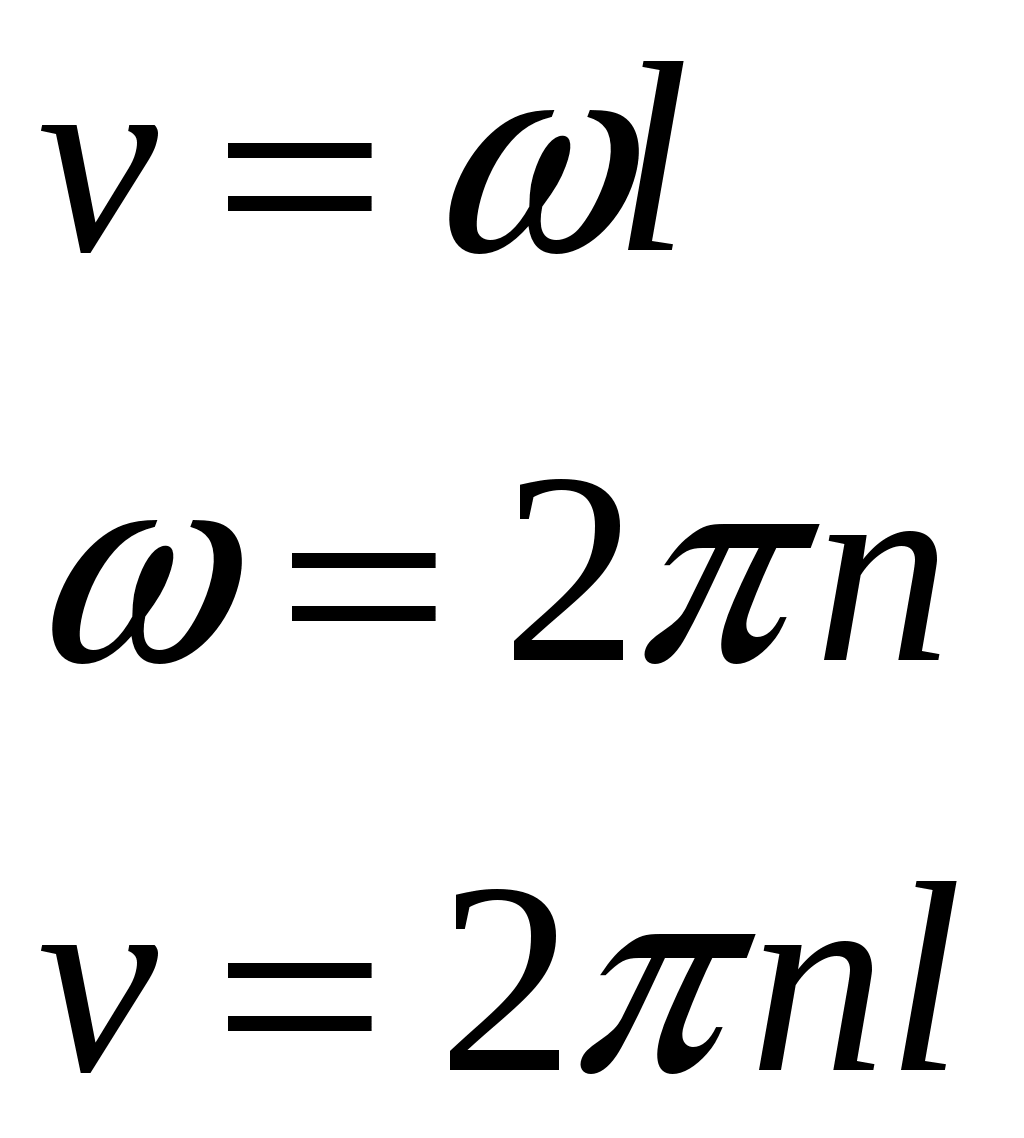|
|
2466_физика_19сен. Решение. Дано Для решения данной задачи используем закон Ома для части электрической цепи
361.Катушка и амперметр соединены последовательно и подключены к источнику тока. К клеммам катушки присоединен вольтметр с сопротивлением г = 4 кОм. Амперметр показывает силу тока I = 0,3 А, вольтметр – напряжение U = 120 В. Определить сопротивление R катушки. Определить относительную погрешность ε, которая будет допущена при измерении сопротивления, если пренебречь силой тока, текущего через вольтметр.
Решение.
Дано:
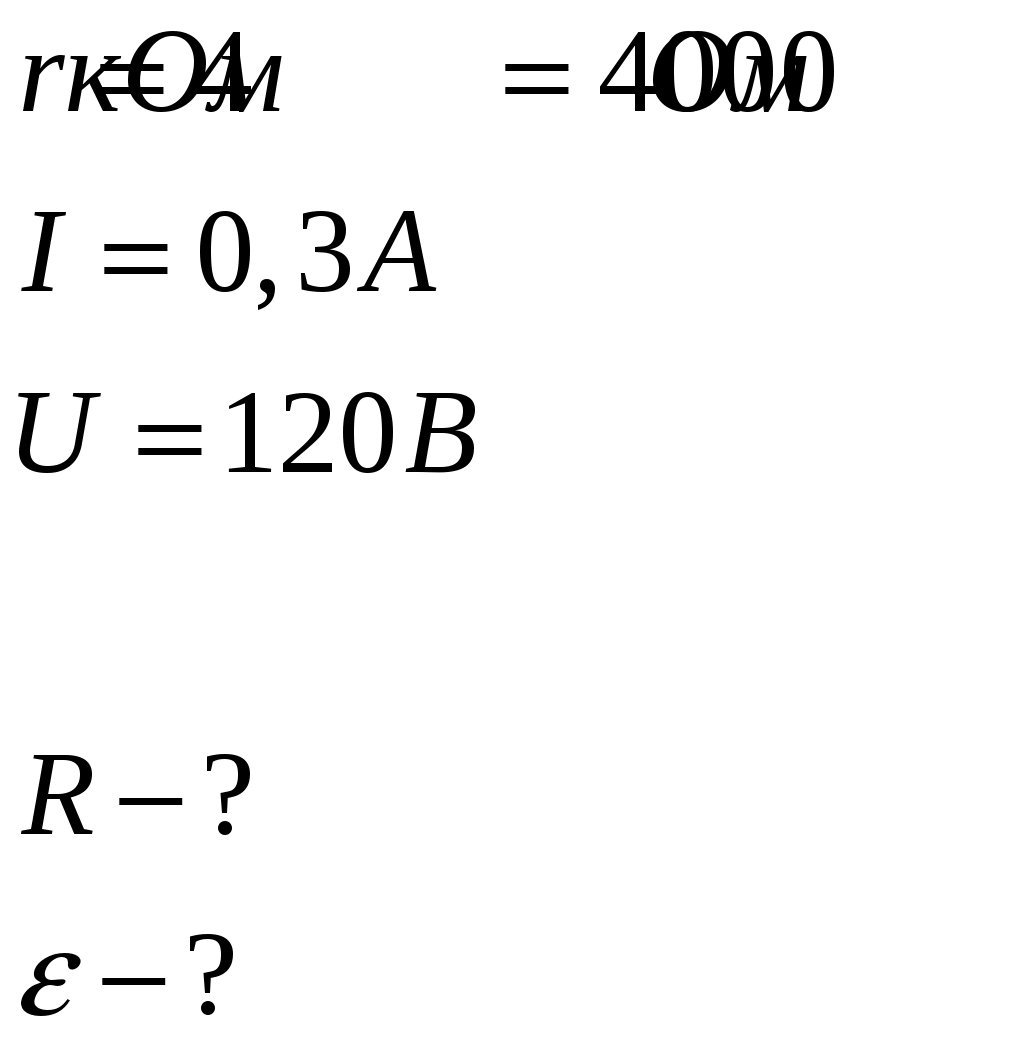
|
Для решения данной задачи используем закон Ома для части электрической цепи:
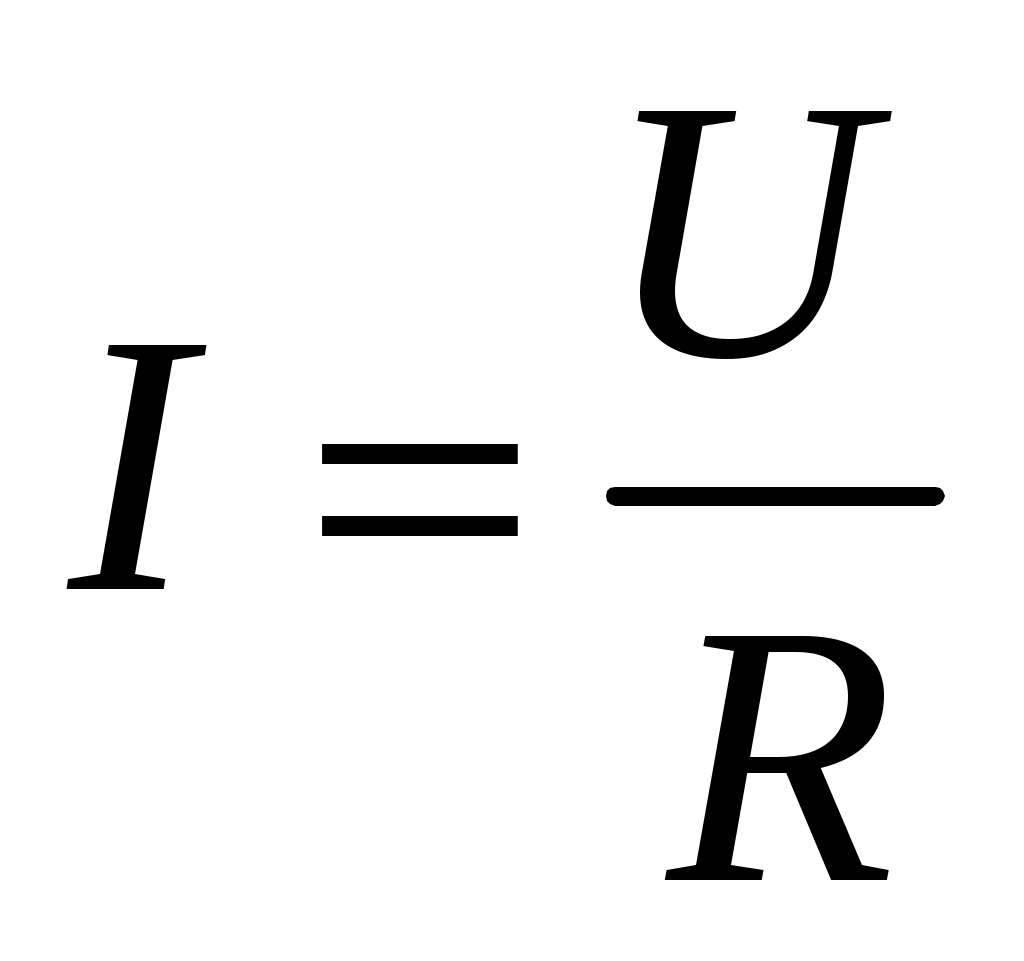
Определим сопротивление катушки в цепи. Поскольку в цепь включен вольтметр с некоторым сопротивлением, то можно считать, что амперметр будет регистрировать суммарный ток как ветки с сопротивлением так и ветки с вольтметром. Тогда можно записать формулу:
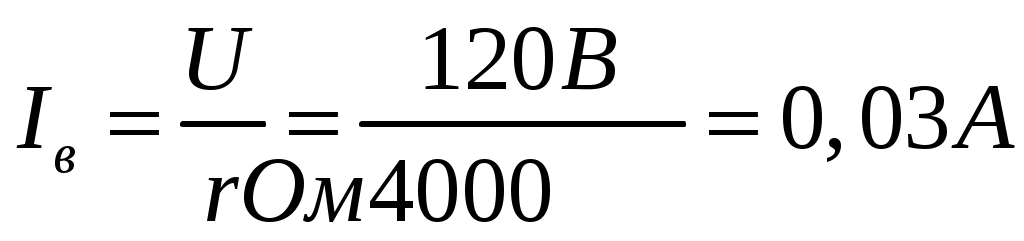
Ток который проходит в ветке с вольтметром равен 0,03А. Тогда по Закону Кирхгофа в неразветвленной цепи мы будем иметь сумму токов. Поэтому можно записать соотношение:
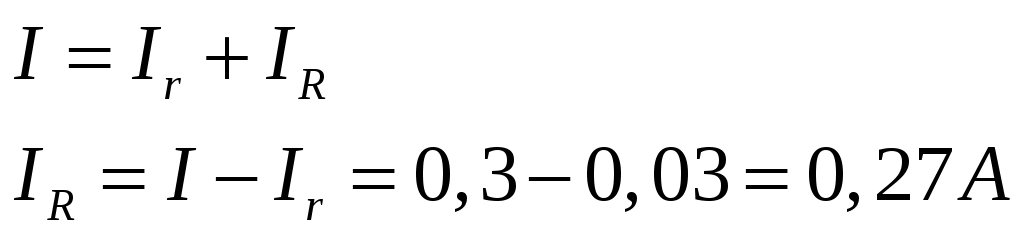
Тогда сопротивление будет равно:
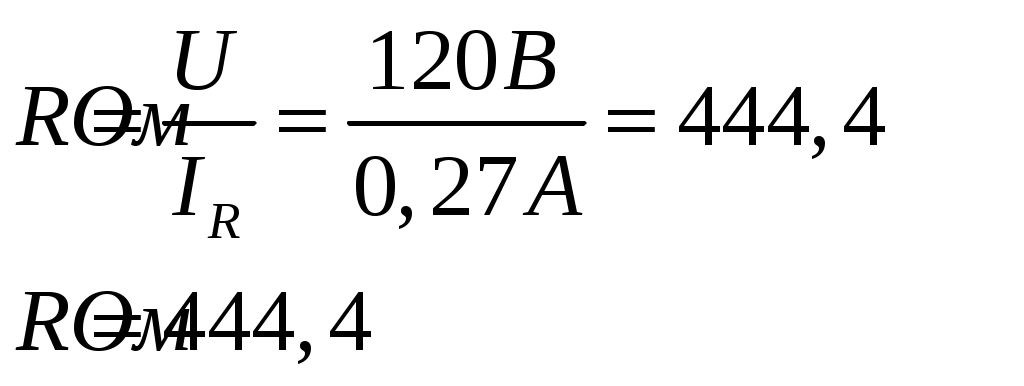
Если считать, что через вольтметр ток не проходит, точнее пренебречь данным током, то можно записать соотношение:
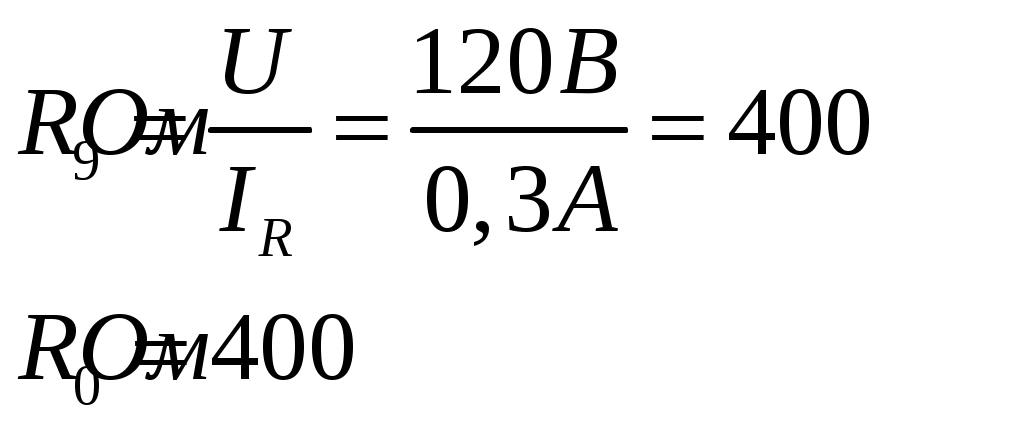
Погрешность измерений буде равна:
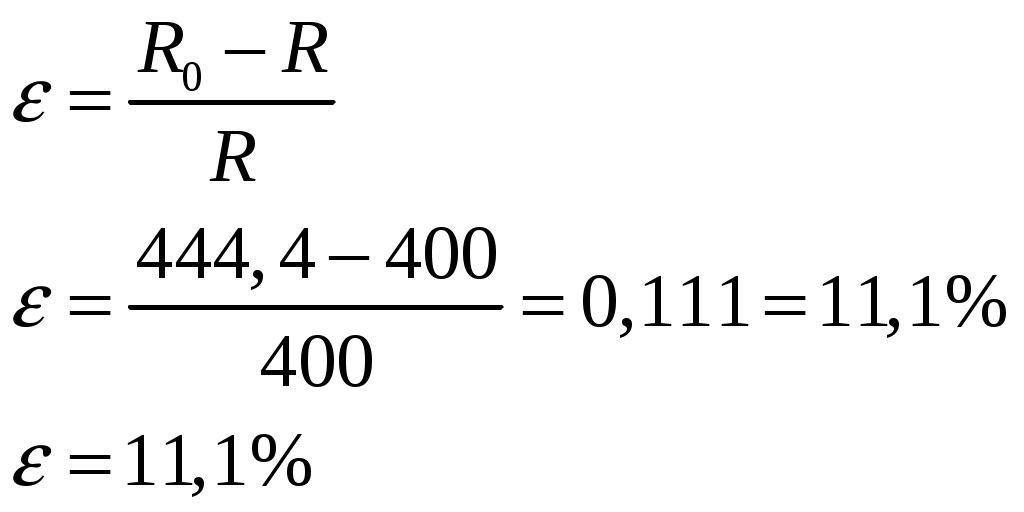
|
Ответ: 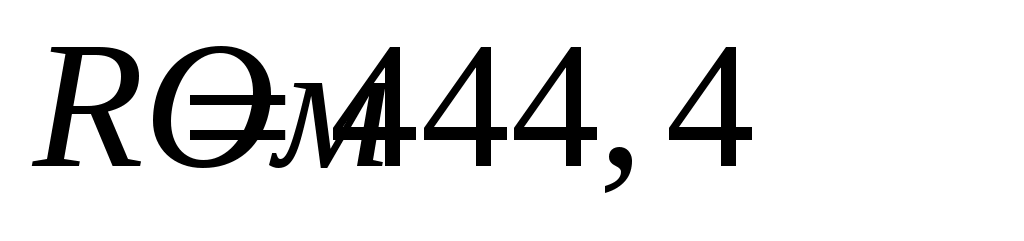 , , 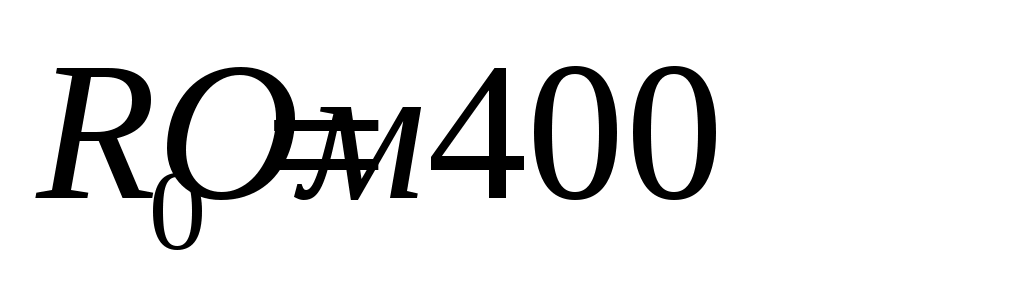 , , 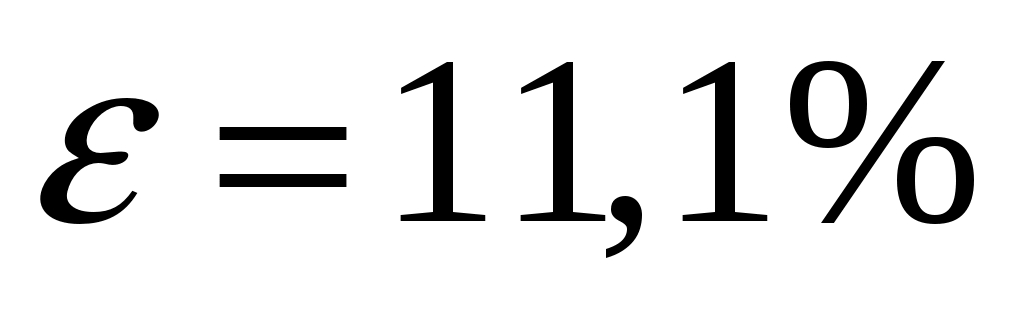 . .
|
371. За время t = 20 с при равномерно возраставшей силе тока от нуля до некоторого значения в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Определить скорость нарастания силы тока, если сопротивление проводника R = 5 Ом.
Решение.
Дано:
t = 20 с
R = 5 Ом
Q = 4 кДж = 4000Дж
V - ?
|
Количество теплоты, которое выделится в контуре равно величине:
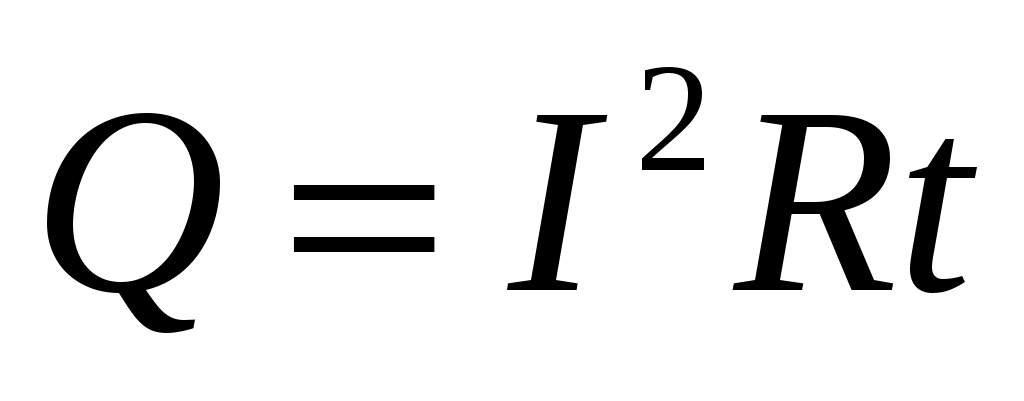
Тогда сила тока которая протекает в контуре будет равна:
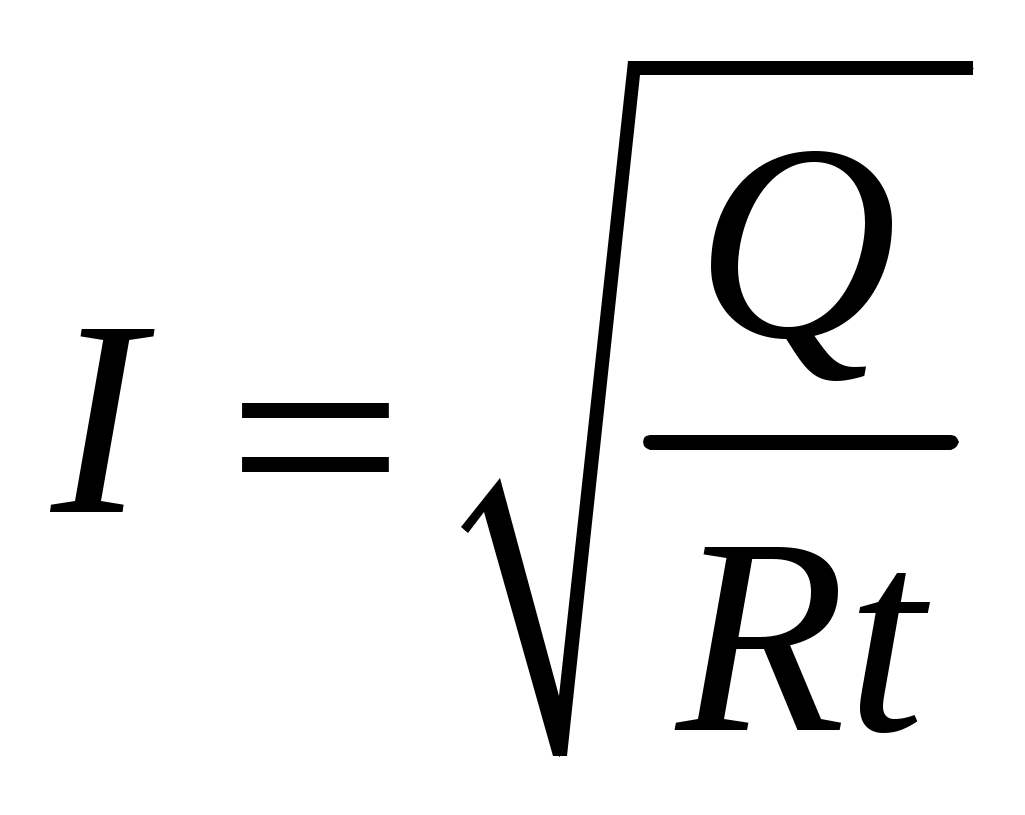
Но таким образом мы найдем только среднее значение силы тока. Подставив значения мы получим:
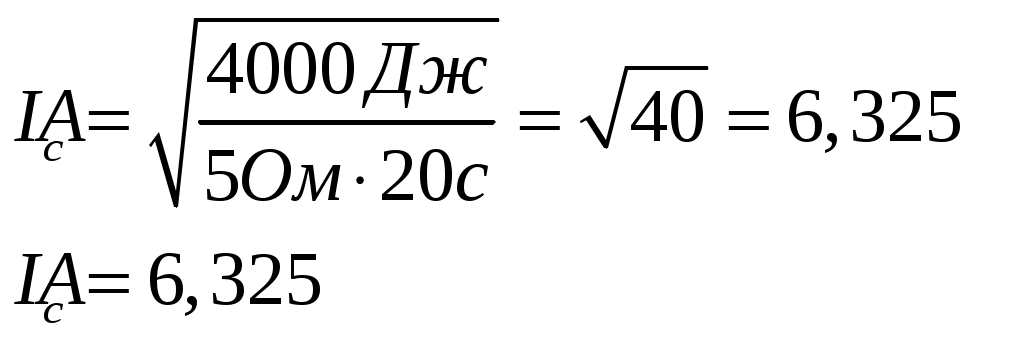
Сила тока изменяется от 0А до значения 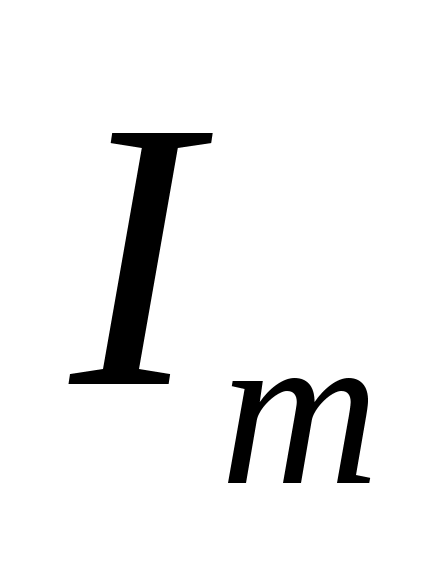 , тогда: , тогда:
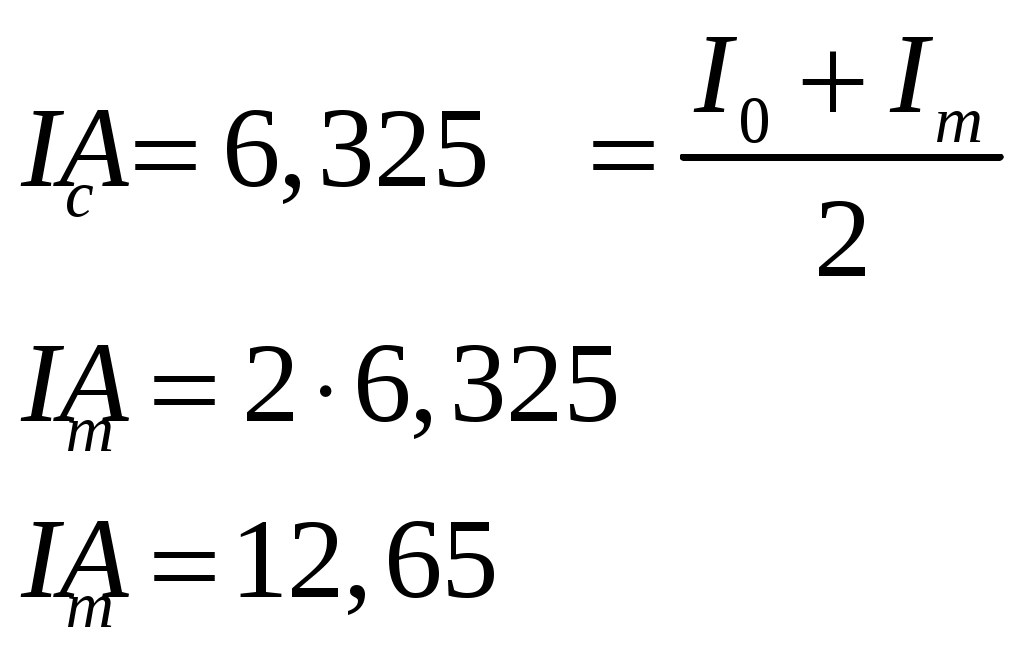
Поскольку нам надо найти скорость возрастания силы тока в цепи, которое зависит от времени, то можно записать соотношение:
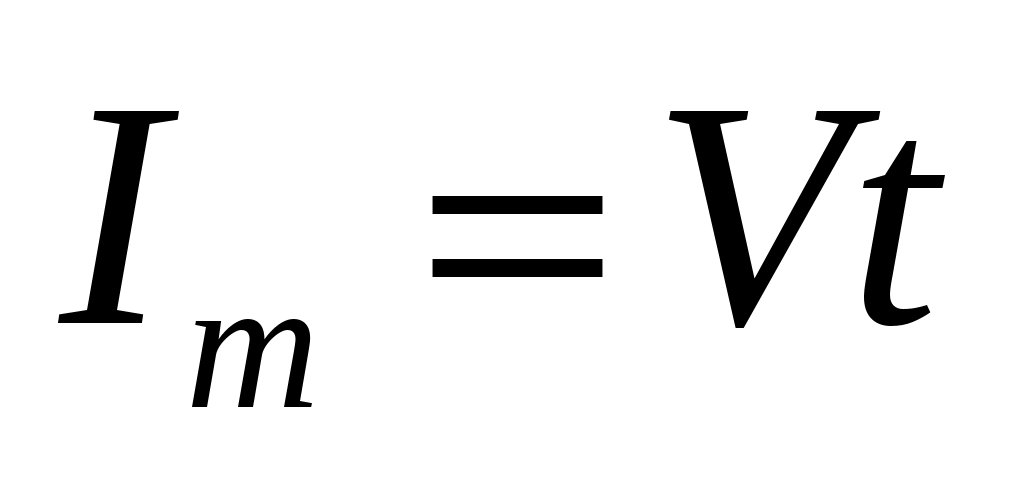
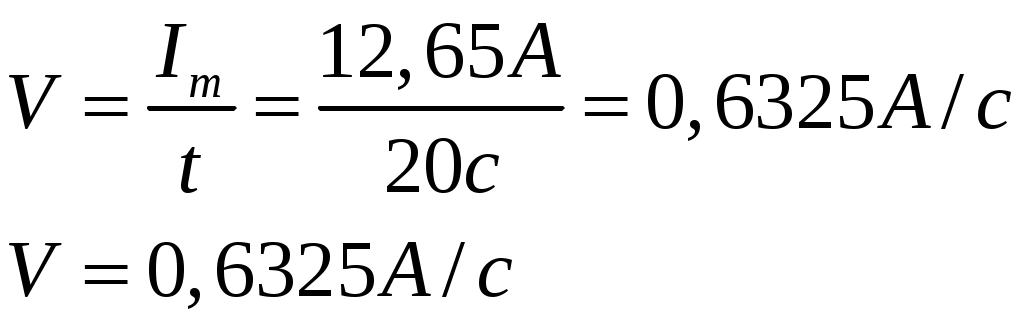
|
Ответ: 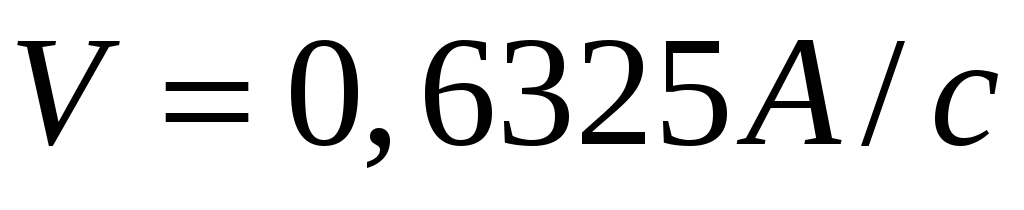
|
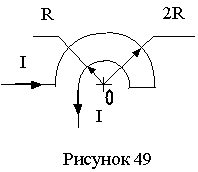
401. Бесконечно длинный провод с током I=100 А изогнут так, как это показано на рис. 49. Определить магнитную индукцию В в точке О. Радиус дуги R= 10 см.
Решение.
Дано:
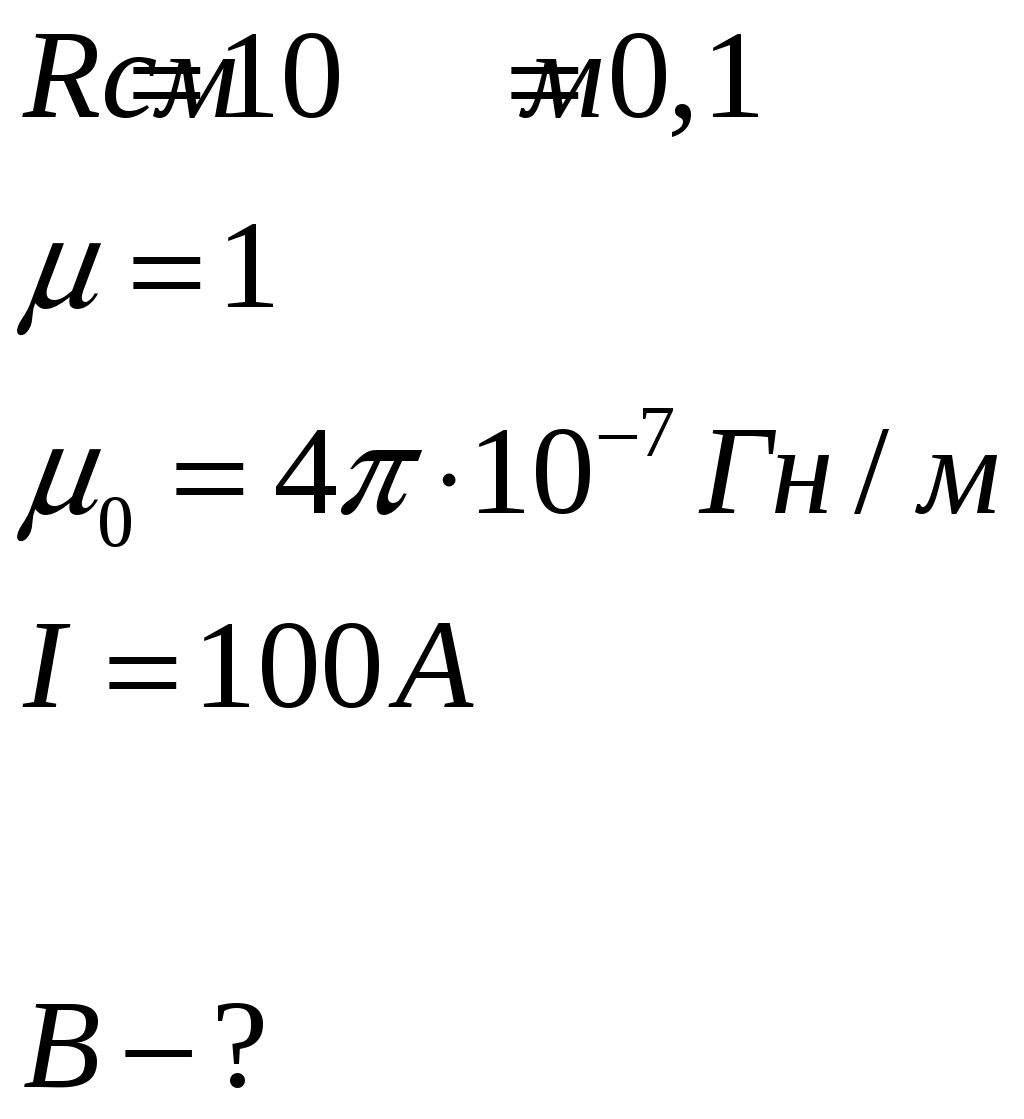
|
Индукция магнитного поля в точке О будет равна сумме индукций поля отдельных участков проводника. Поэтому мы можем разбить проводник на несколько участков, тогда суммарная индукция будет равна:
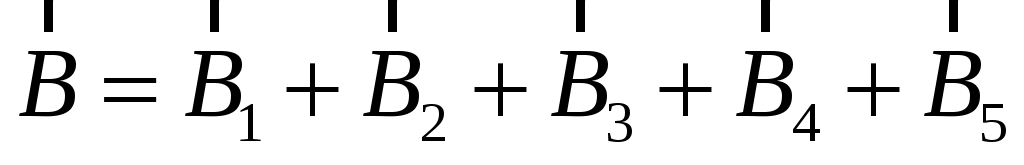
Или в скалярном виде:
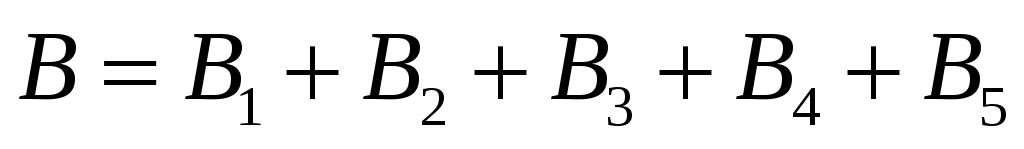
На приведенном рисунке мы отобразили каждый из указанных участков:

При рассмотрении рисунка можно сделать выводы, что участки 1 и 3 лежат на оси полукруга и на одной линии с точкой О, поэтому их вклад в суммарное значение индукции магнитного поля равно нулю:
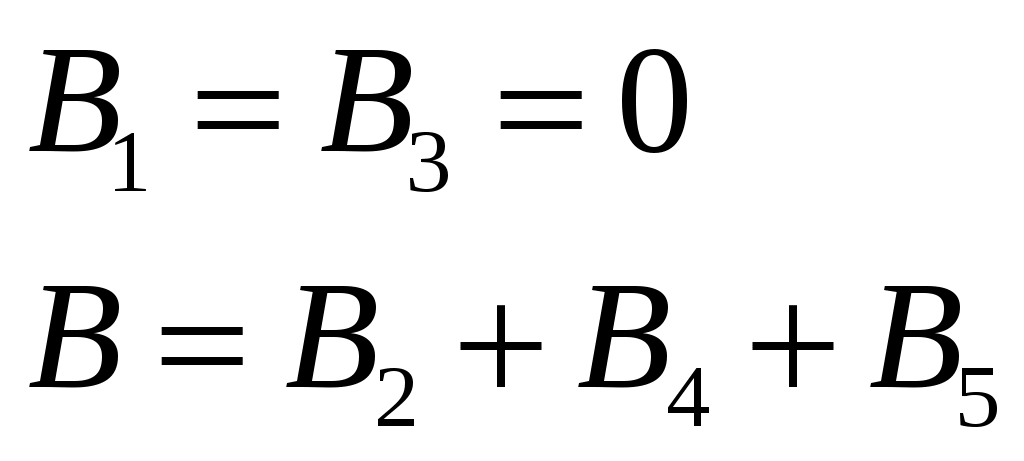
Индукция полукольца будет равна:
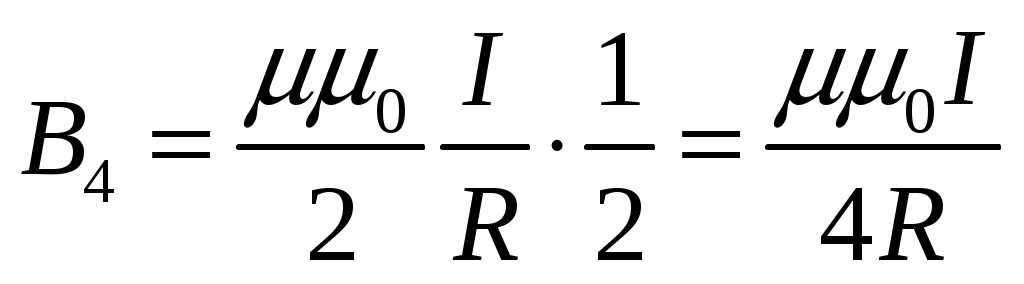 и и 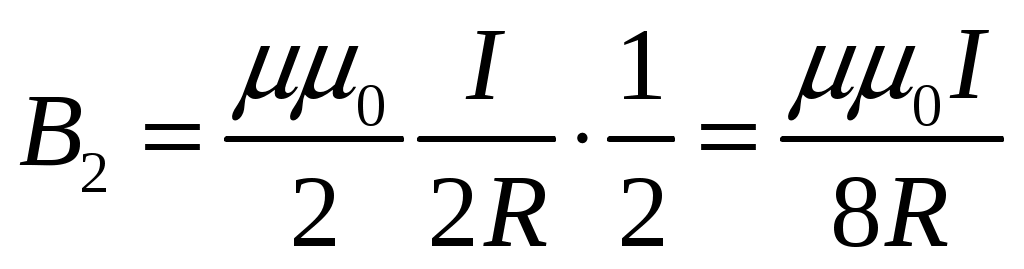
Индукция для участка 5 будет равна:
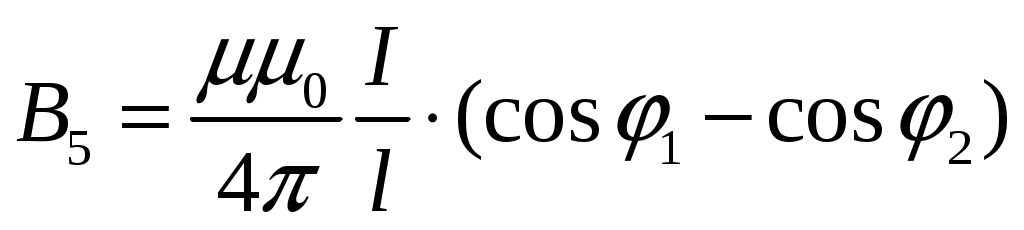
Поскольку из рисунка видно, что: 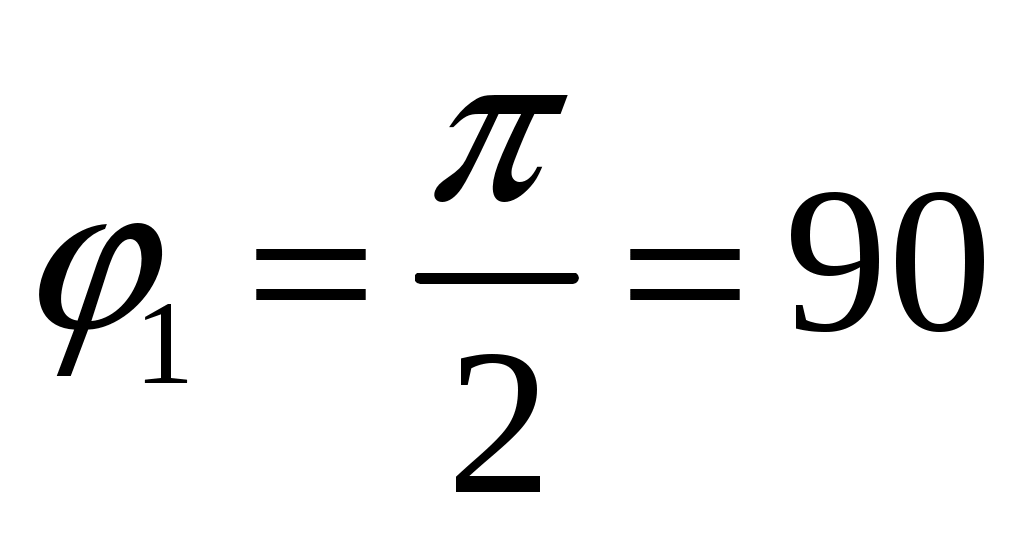 , а , а 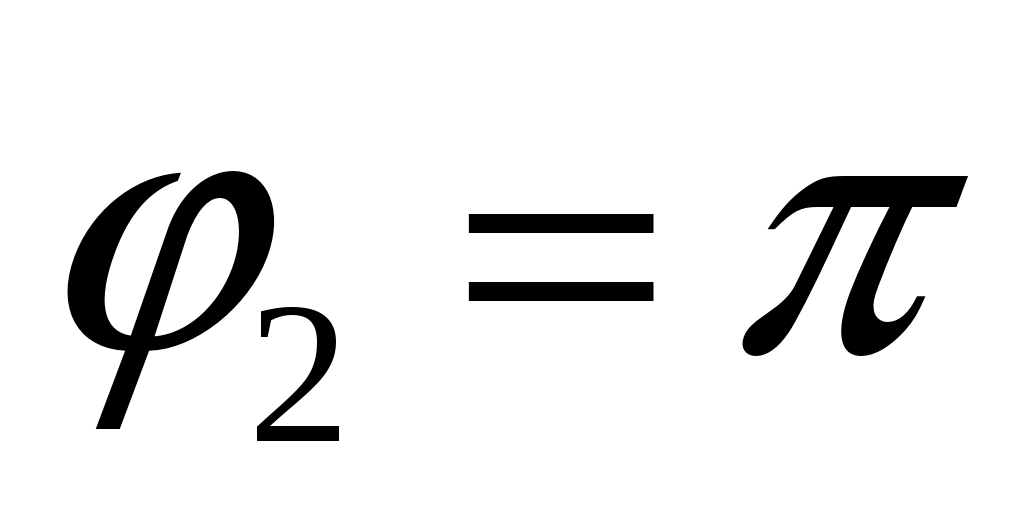 , то: , то:
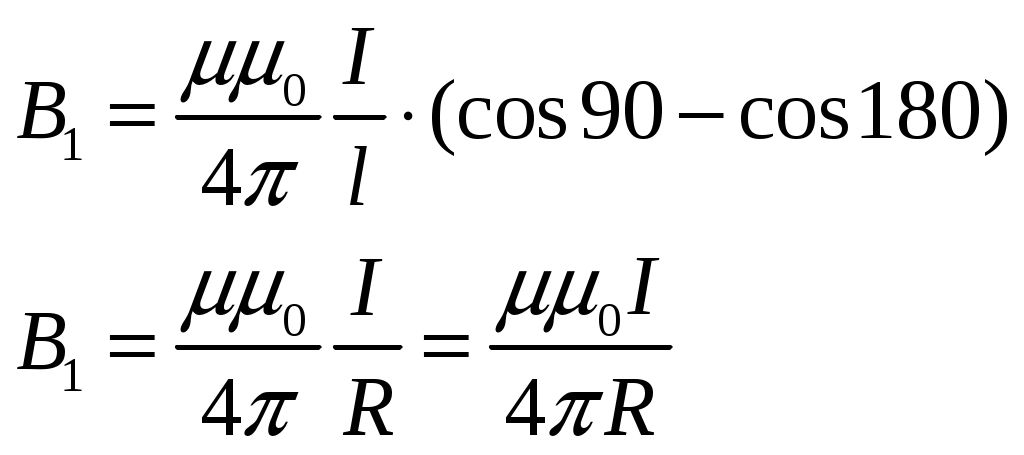
Тогда результирующее значение индукции магнитного поля равно:
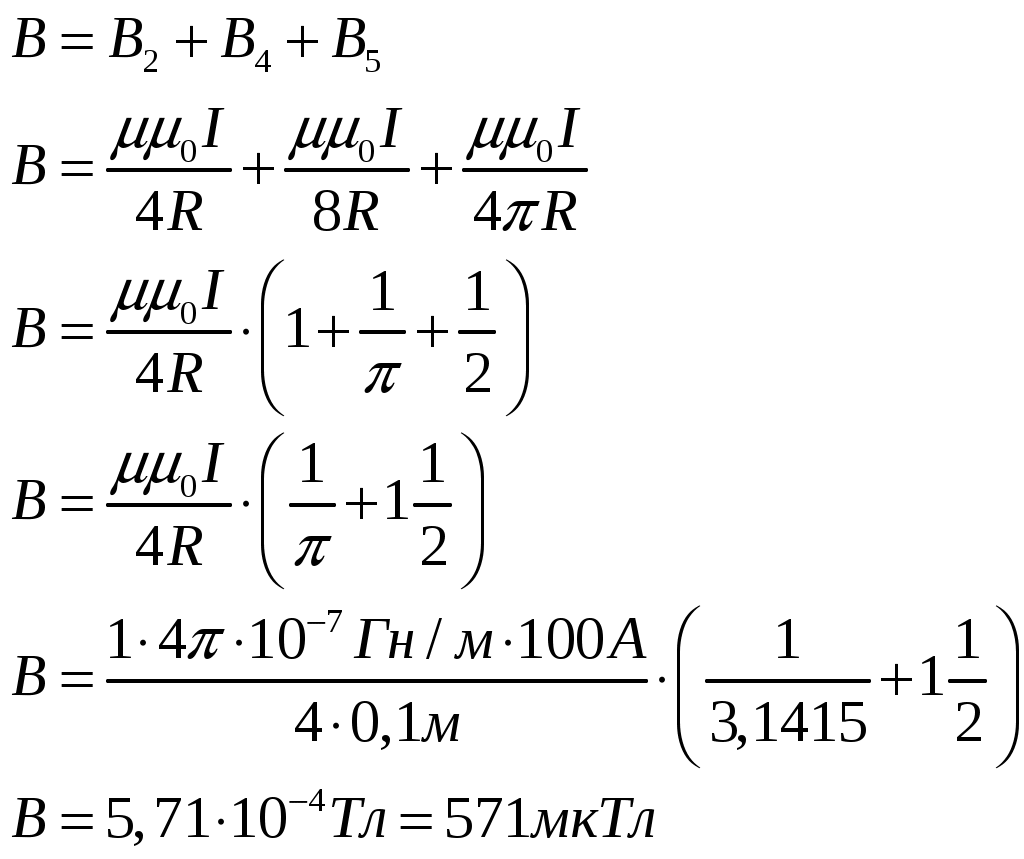
Индукция магнитного поля в некоторой точке О поля будет равна 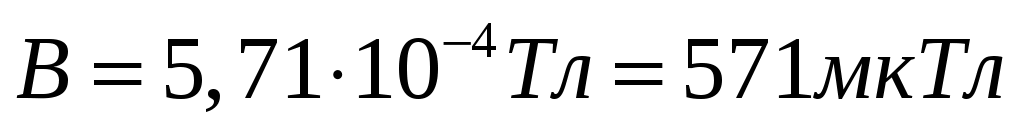 . .
|
Ответ: 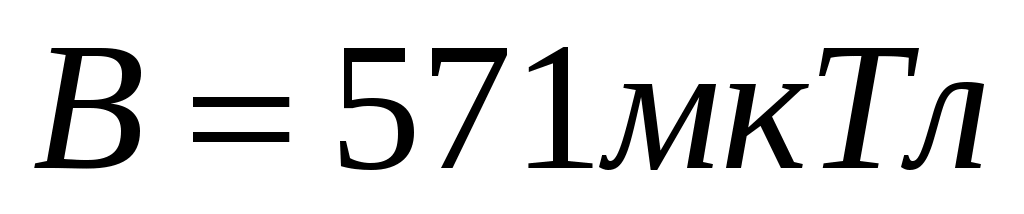 . .
|
411. По двум параллельным проводам длиной l = 3м каждый текут одинаковые токи I= 500 А. Расстояние d между проводами равно 10см. Определить силу F взаимодействия проводов.
Решение.
Дано:
l = 3м
I= 500 А
D=0,1 м
F - ?
|
Сила взаимодействия двух проводников с током будет равна:
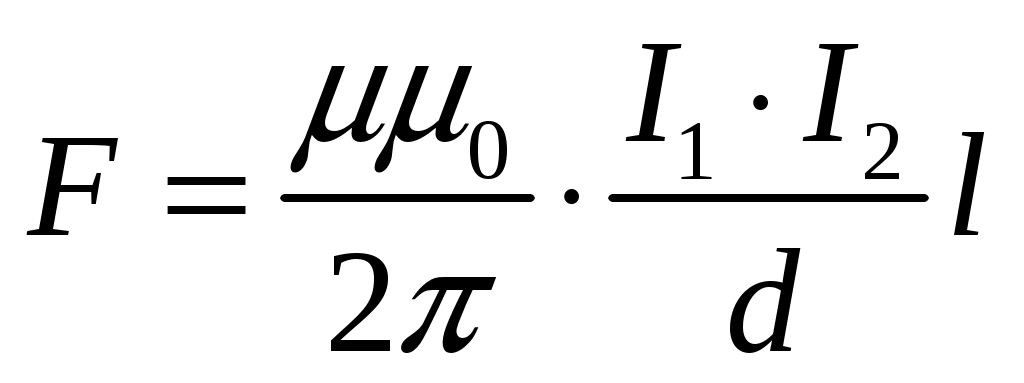
Подставим числовые данные в полученную формулу:
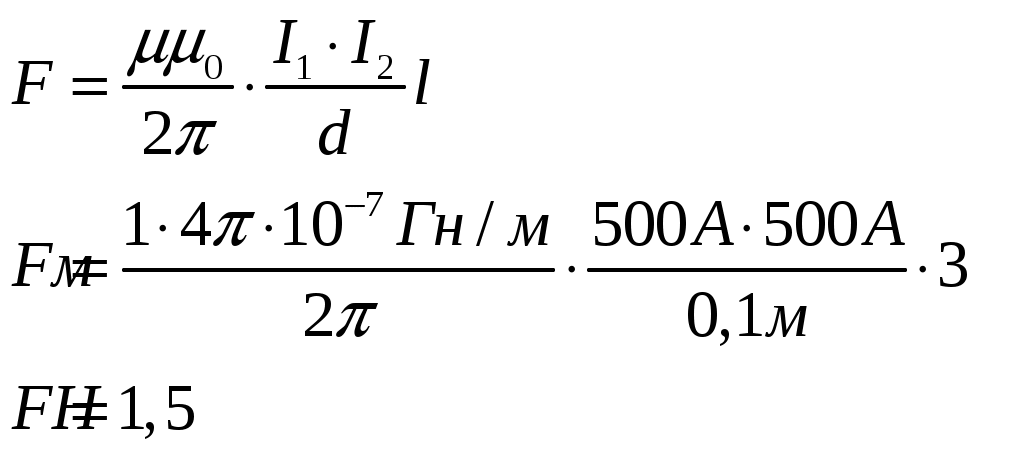
|
Ответ: 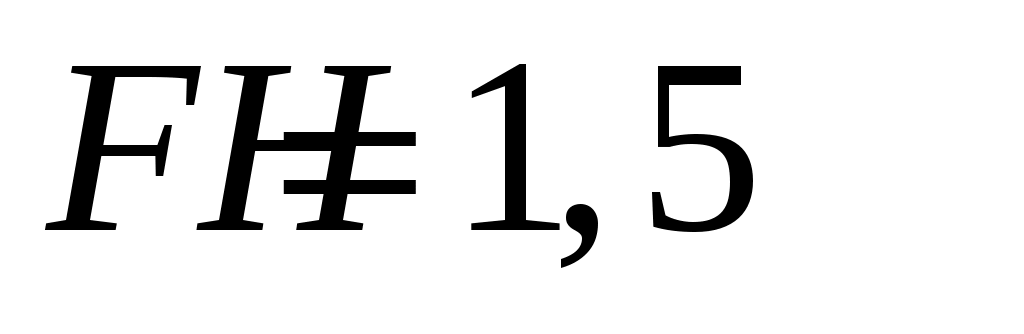 . .
|
431. Два иона разных масс с одинаковыми зарядами влетели в однородное магнитное поле, стали двигаться по окружностям радиусами R1 = 3 см и R2=1,73 см. Определить отношение масс ионов, если они прошли одинаковую ускоряющую разность потенциалов.
Решение.
Дано:
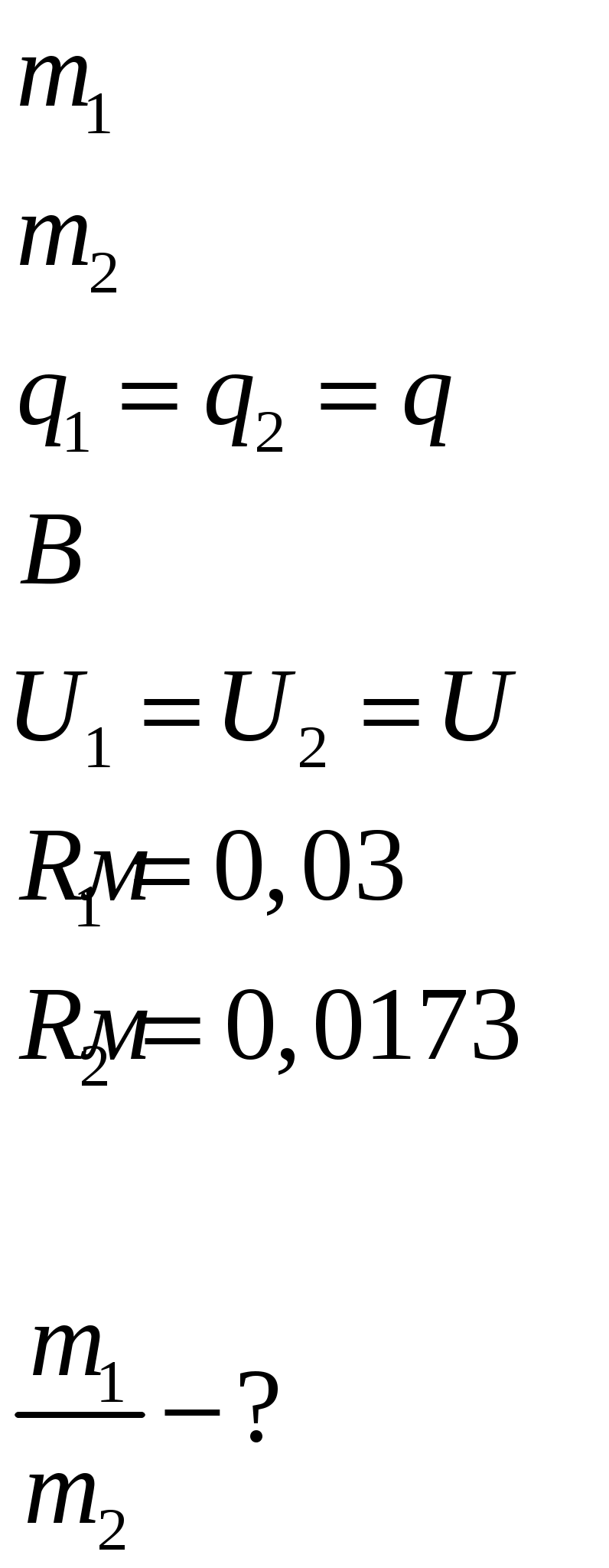
|
Поскольку ионы прошли ускоряющую разницу потенциалов величиной U, то можно записать соотношение для закона сохранения энергии:
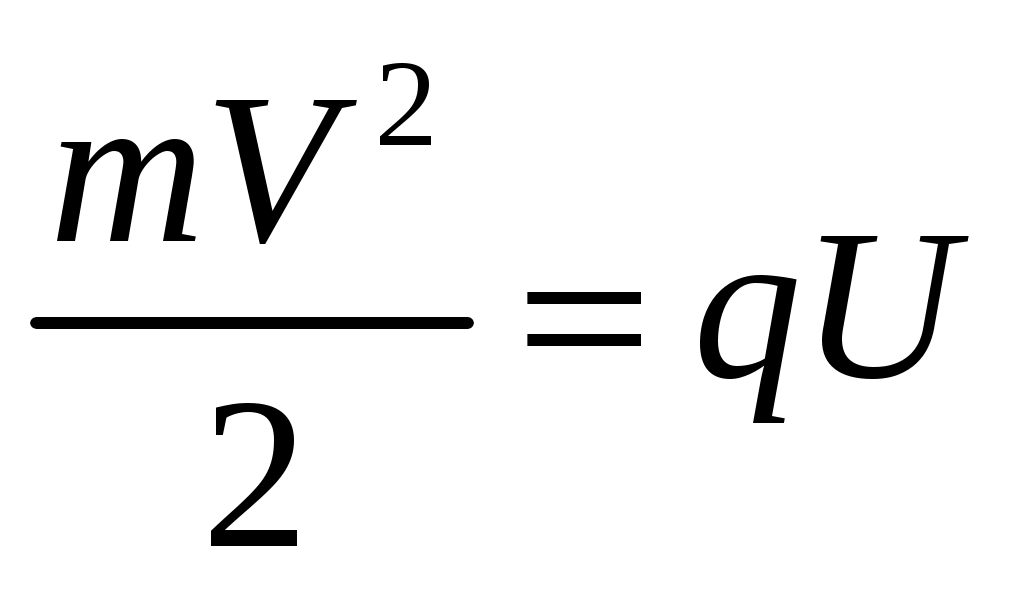
Скорость микрочастиц будет тогда равна:
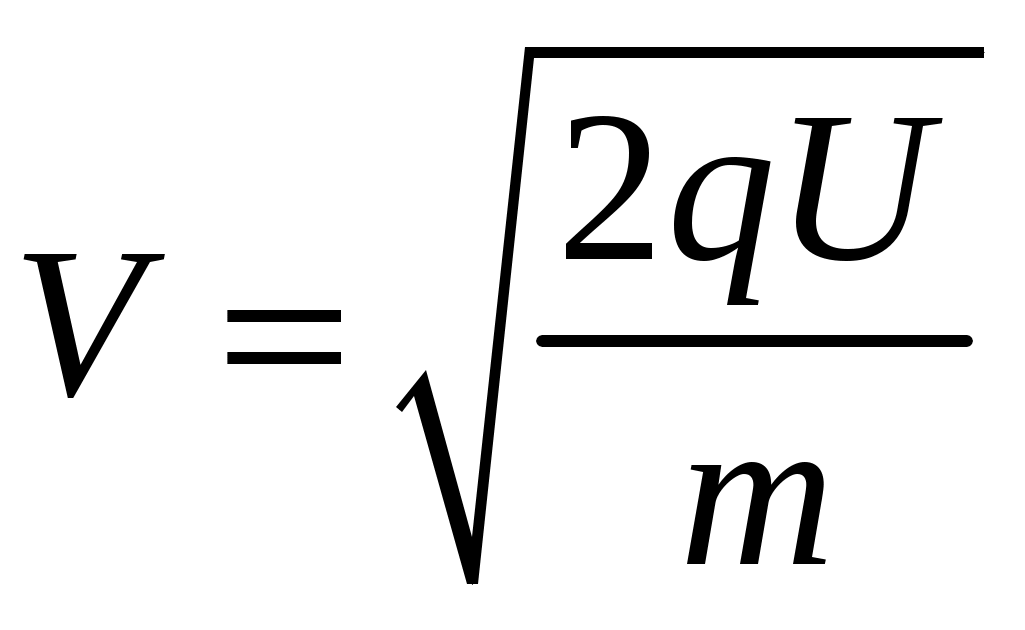
Тогда их скорости будут равны с учетом того, что 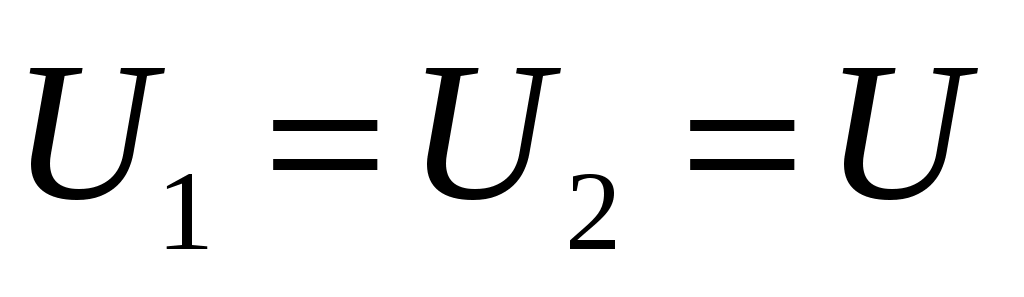 и и 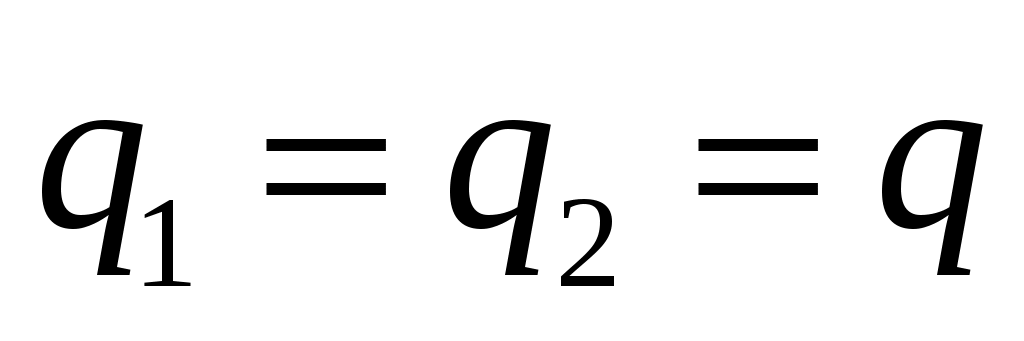 : :
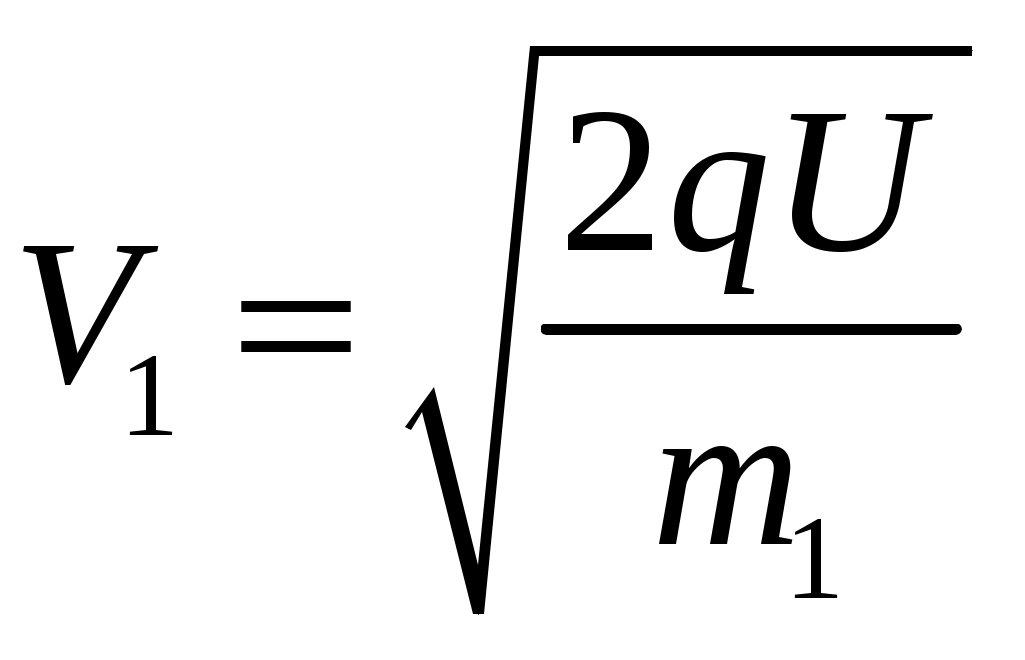 и и 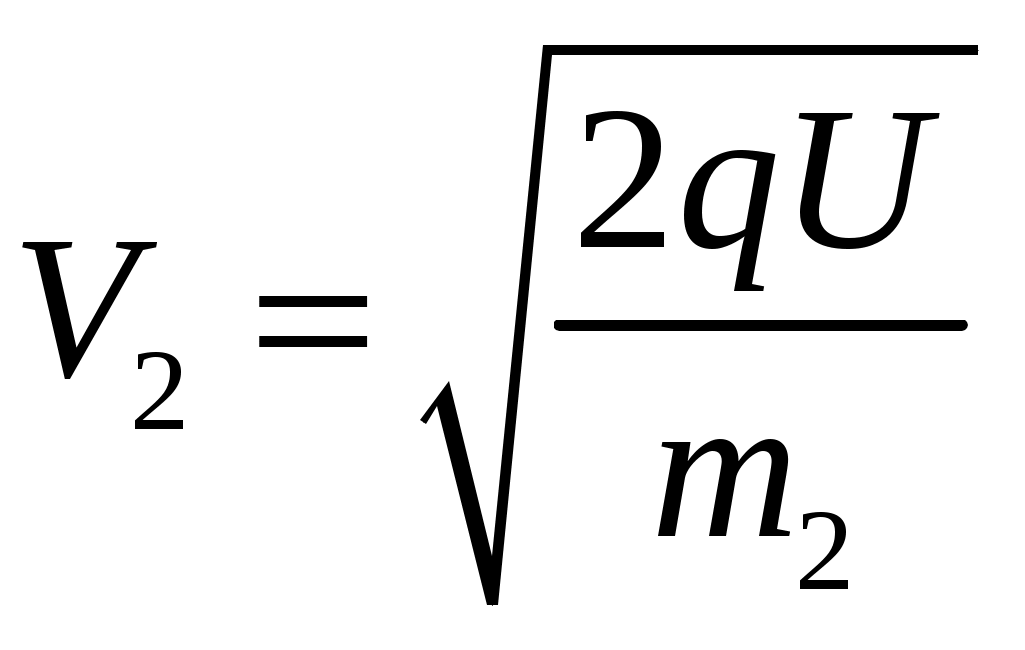 . .
В однородном магнитном полу микрочастицы будут двигаться по спирали и для этого случая можно записать второй закон Ньютона:
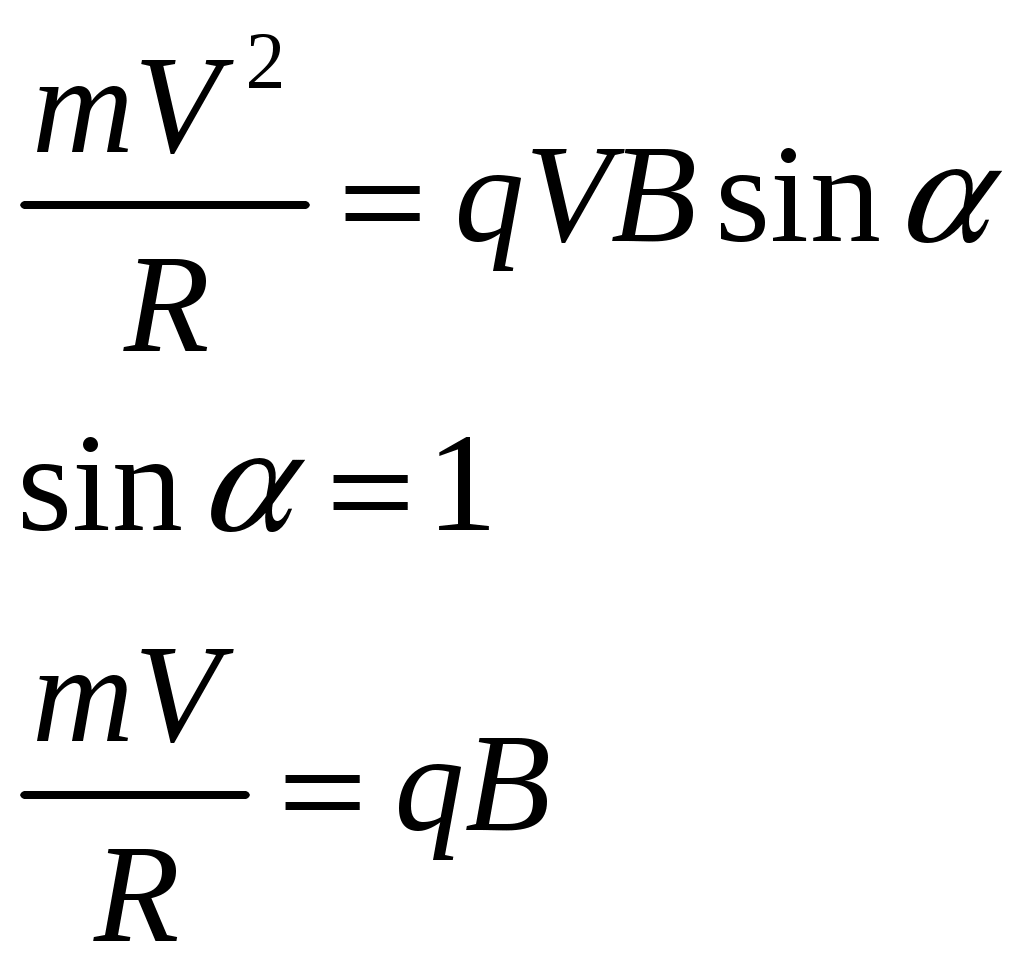
Тогда для двух микрочастиц разной массы мы запишем:
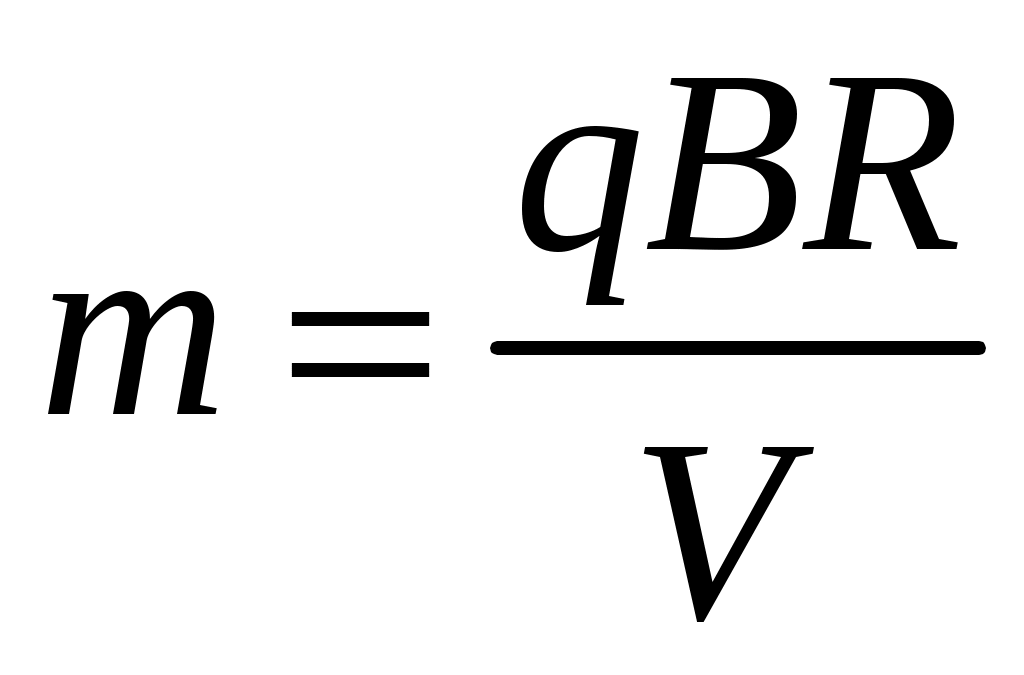 и и 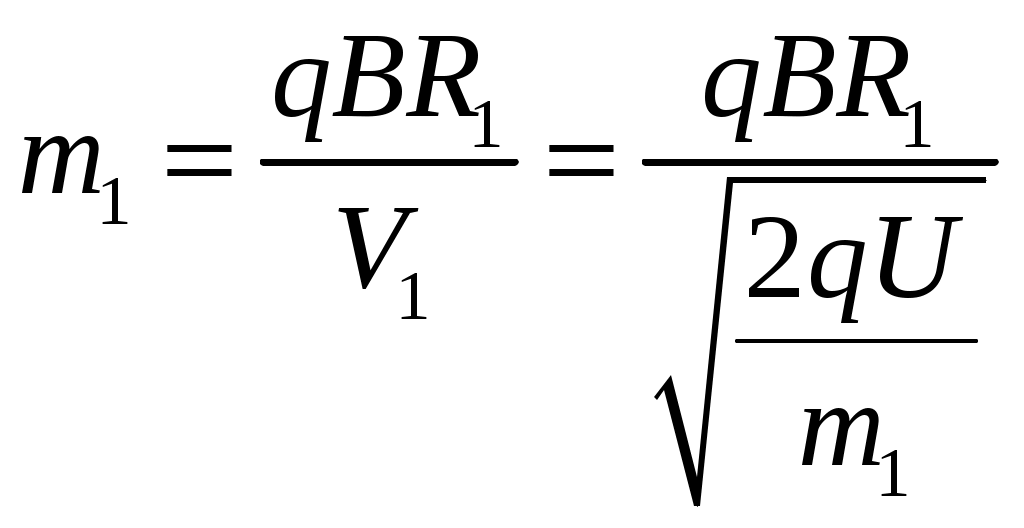 и для второй и для второй 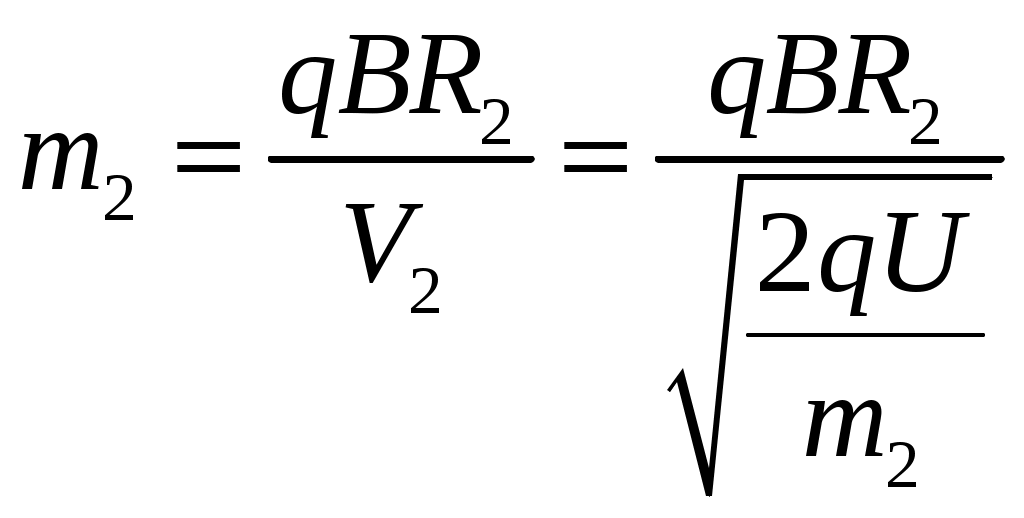 . .
Найдем соотношение масс микрочастиц:
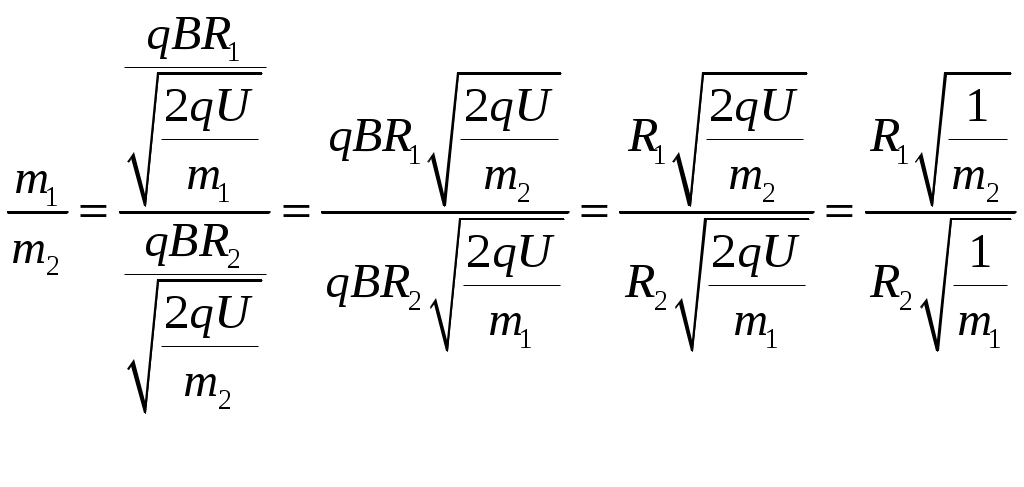
Упростим формулу:
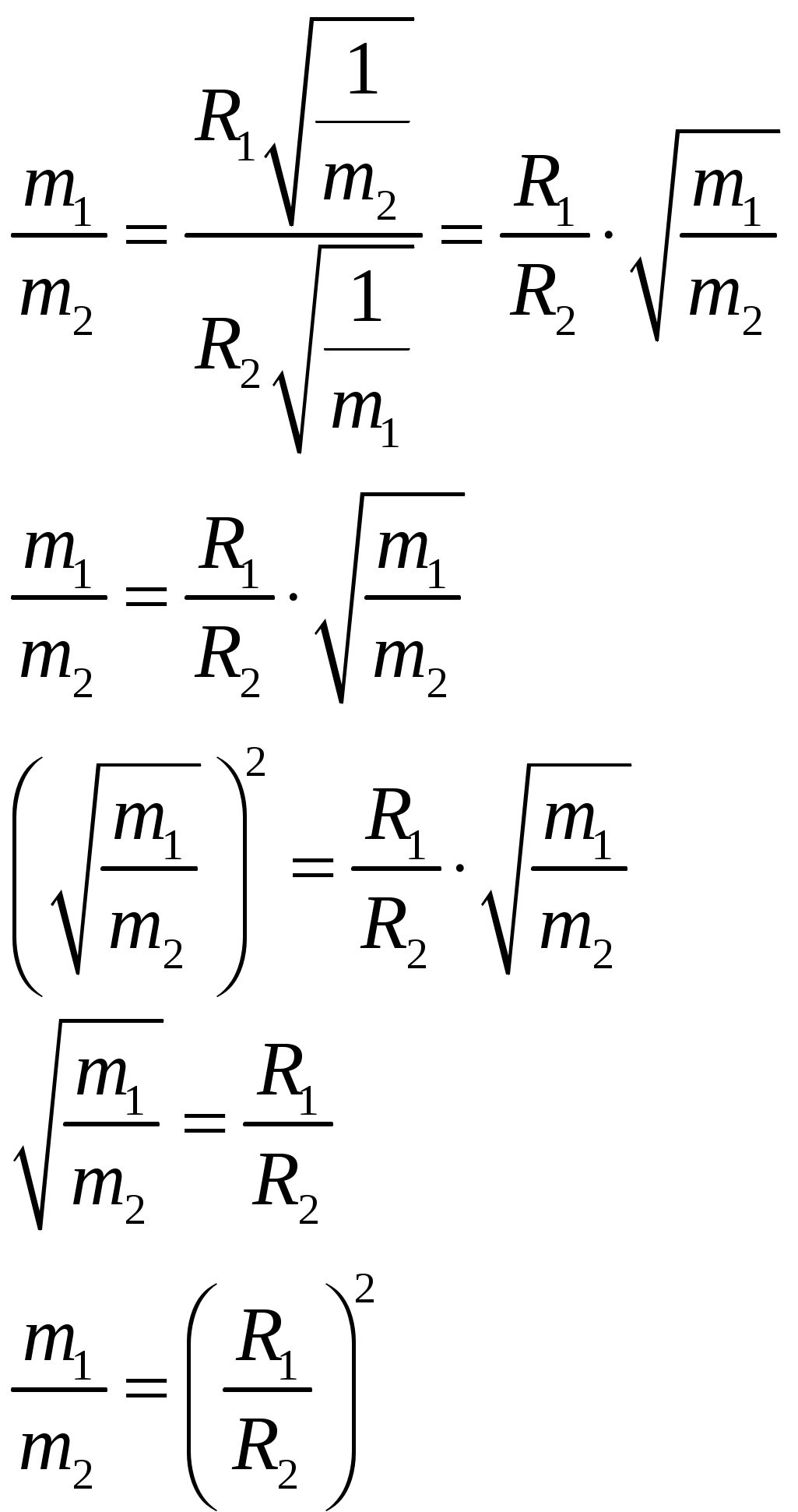
Подставим числовые данные в полученную формулу:
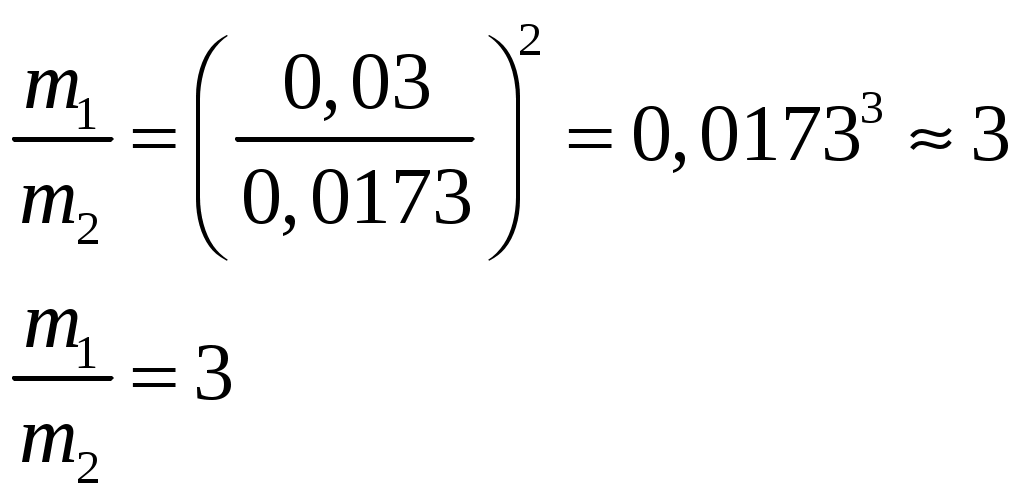
|
Ответ: 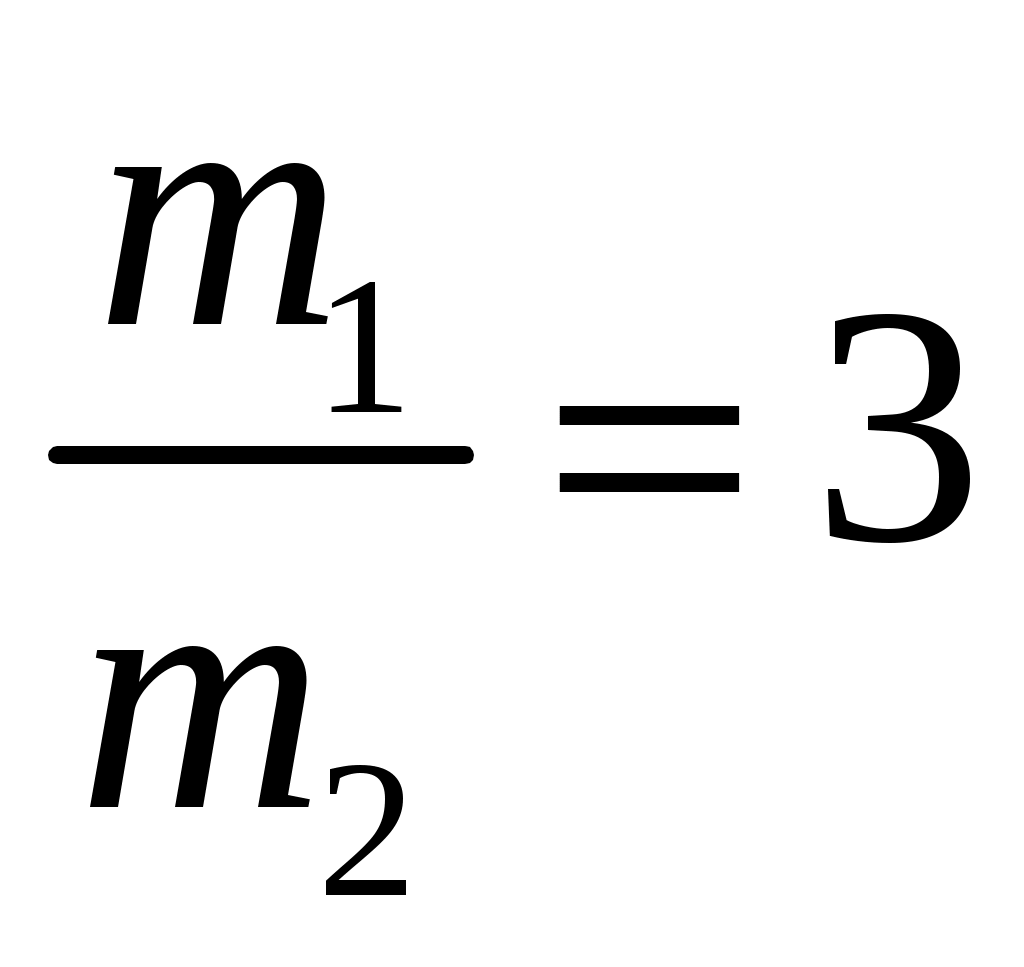 . .
|
441. Протон влетел в скрещенные под углом α= 120° магнитное (В = 50 мТл) и электрическое (Е = 20 кВ/м) поля. Определить ускорение а протона, если его скорость v (|v| = 4ּ105 м/с) перпендикулярна векторам Е и В.
Решение.
Дано:
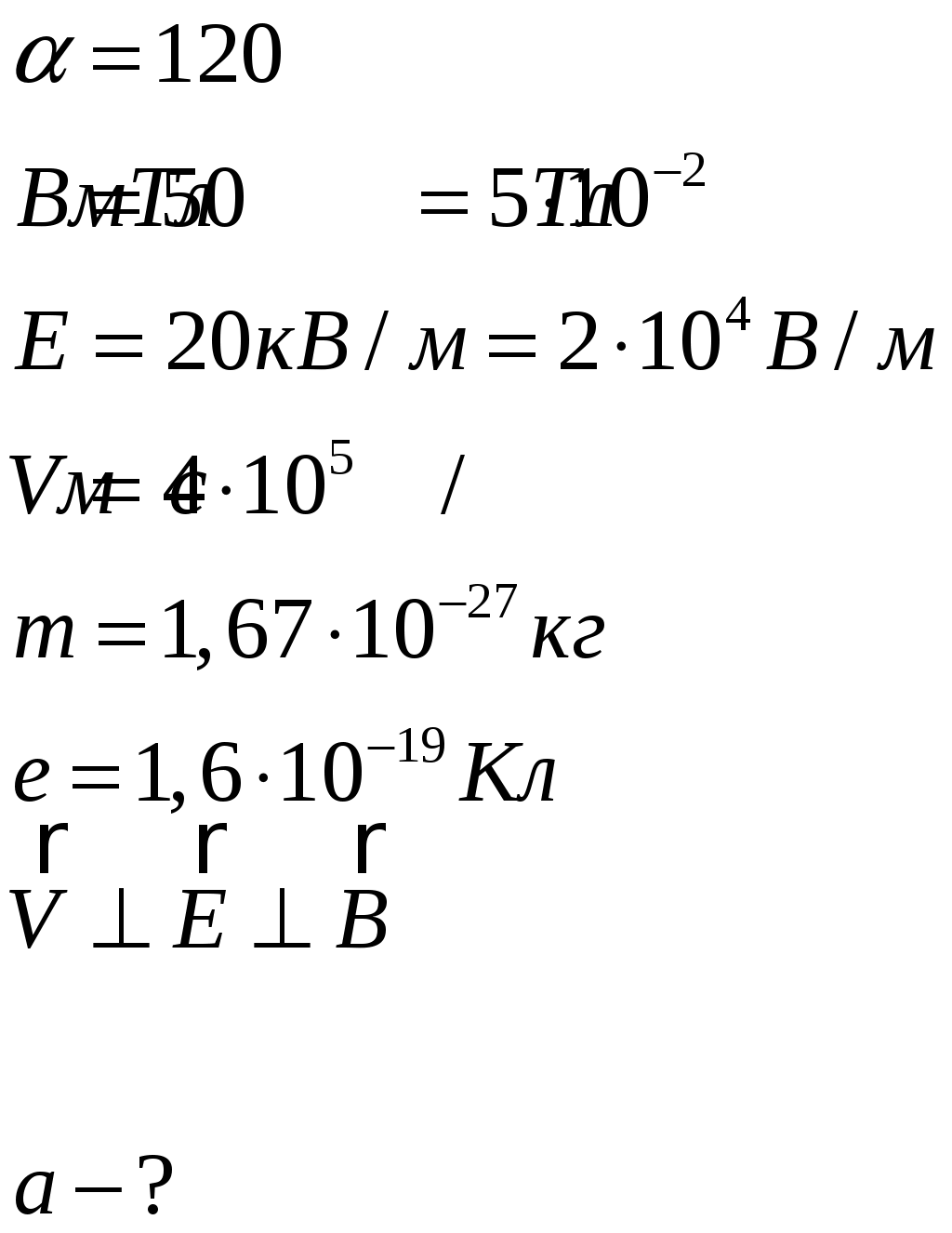
|
По условию задачи частица будет двигаться в скрещенных под углом в 120° магнитном и электрическом полях. Поэтому у протона возникнет ускорение. Причем возникнет как центростремительное ускорение, так и ускорение под действием электрического поля.
Поэтому результирующее ускорение частицы будет согласно законов физики равно:
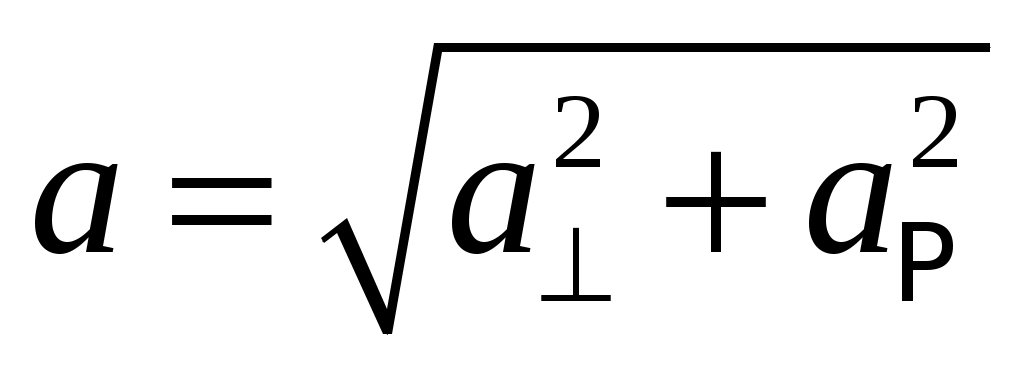 (1). (1).
В электрическом поле на частицу действуют сила Кулона:
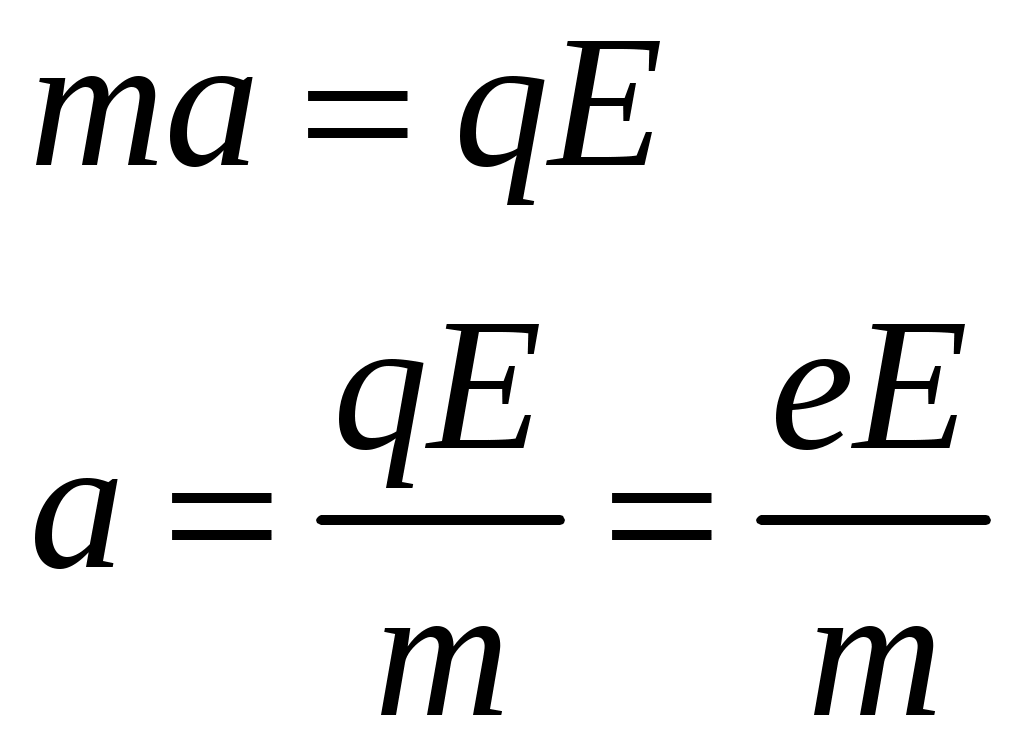
Если учесть, что электрическое и магнитное поля скрещены под углом, то:
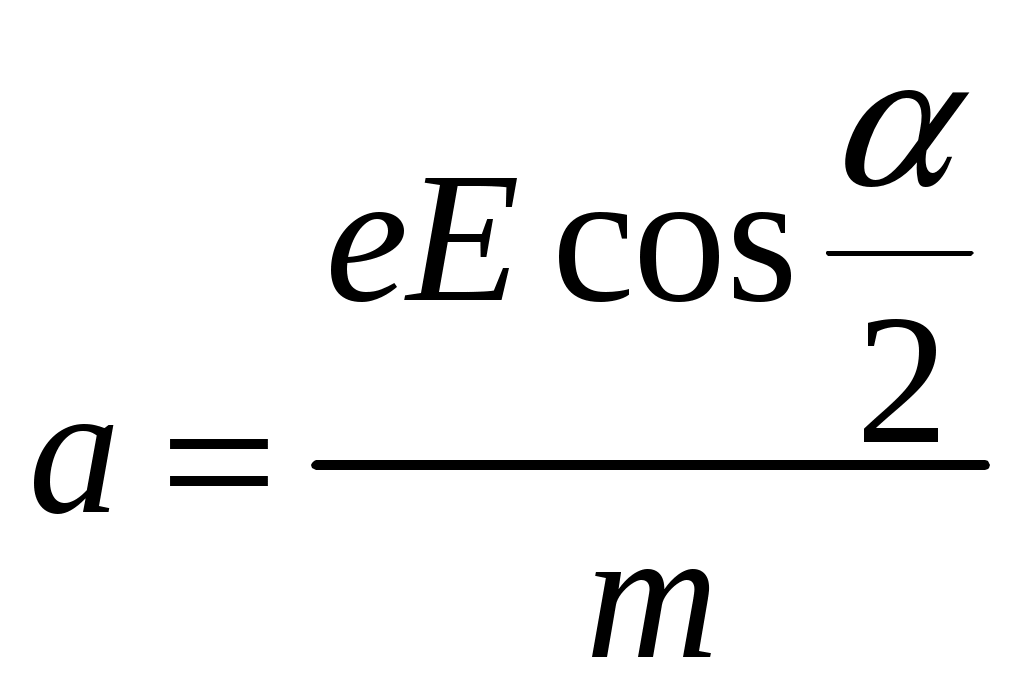
В магнитном поле протон, как и любая заряженная частица будет двигаться по винтовой линии.
Сила Лоренца действует на него в плоскости перпендикулярной вектору индукции магнитного поля и придает ему центростремительное ускорение.
Тогда можно записать:
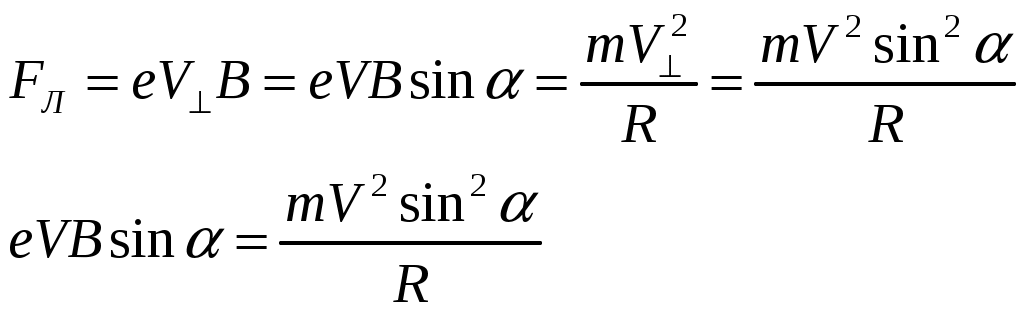
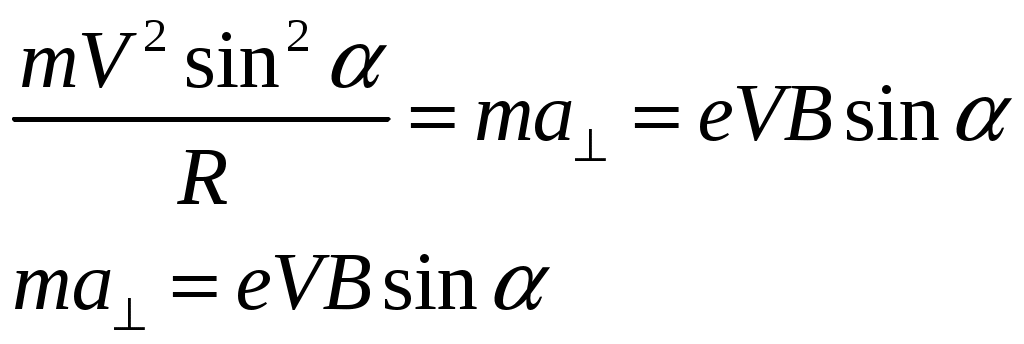
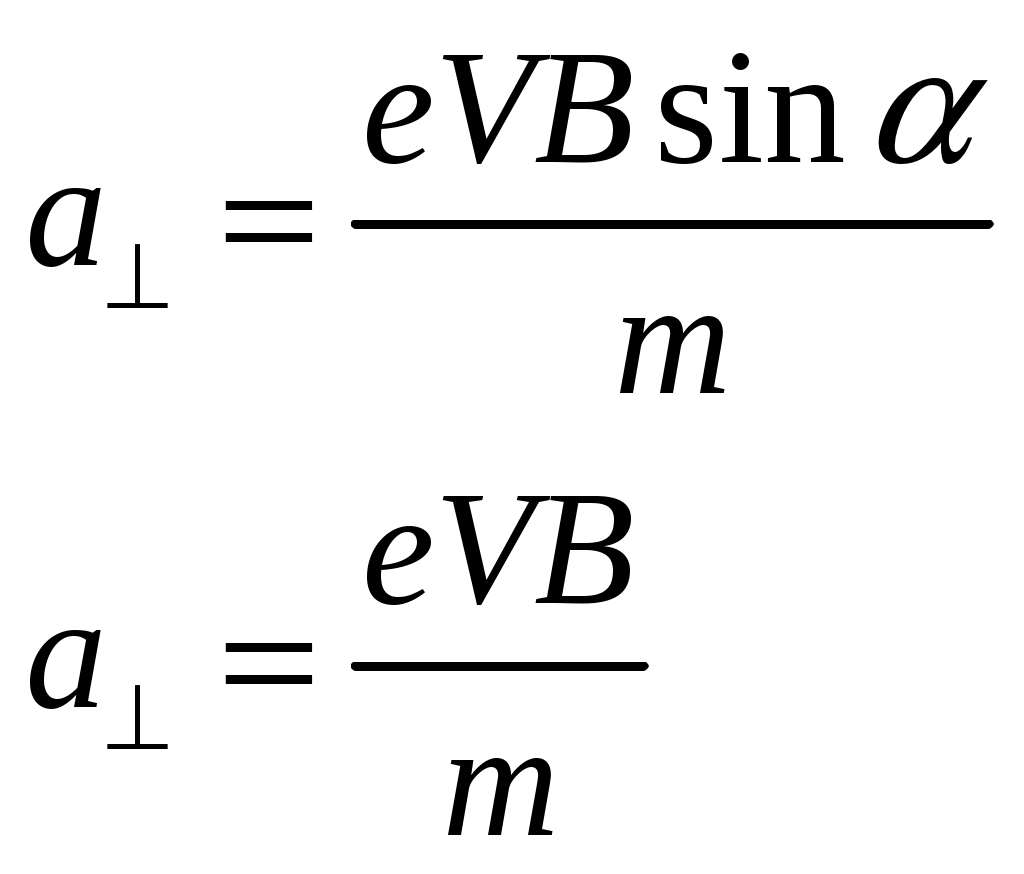
Тогда согласно формулы (1) мы можем записать соотношение для нахождения результирующего ускорения системы.
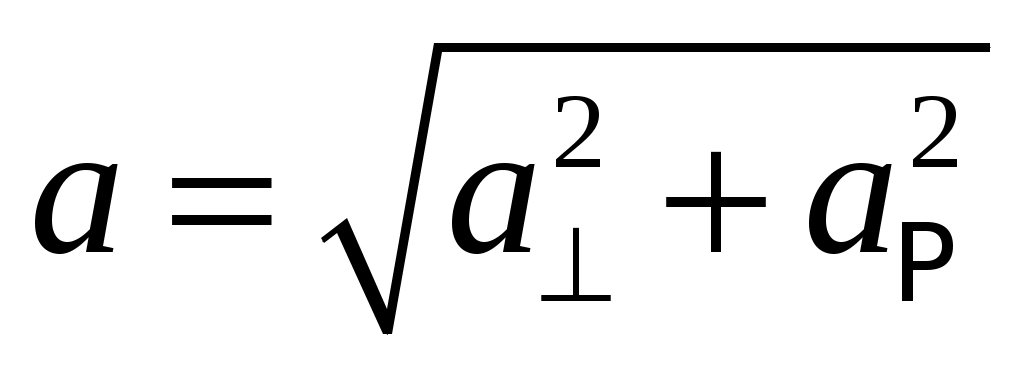
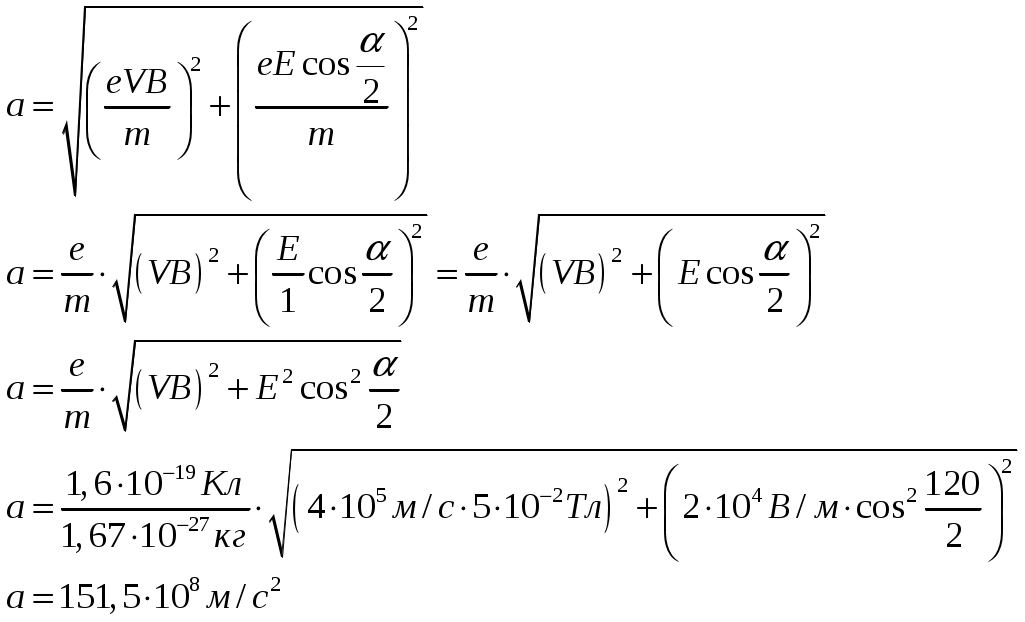
|
Ответ: 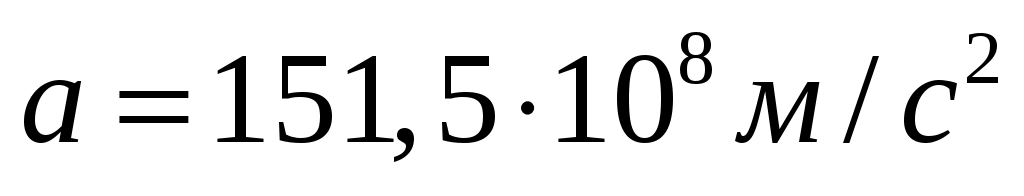 . .
|
451. Плоский контур площадью S = 20 см2 находится в однородном магнитном поле (В = 0,0ЗТл). Определить магнитный поток Ф, пронизывающий контур, если плоскость его составляет угол φ=60° с направлением линий магнитной индукции.
Решение.
Дано:
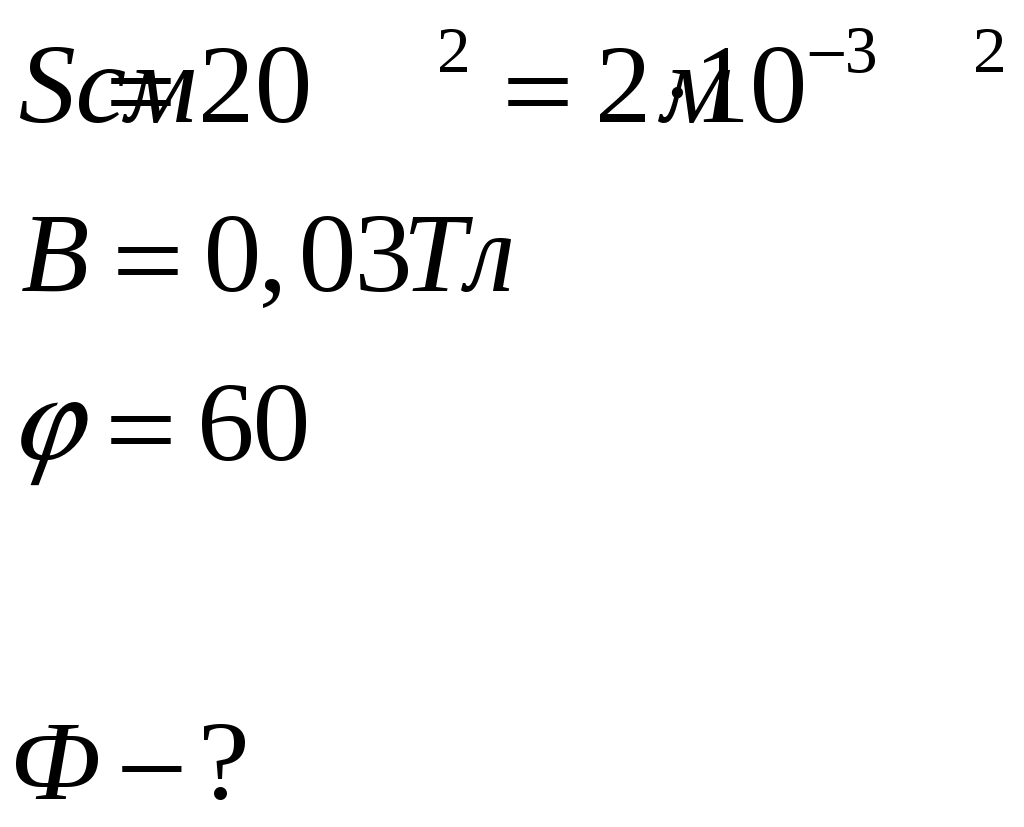
|
Магнитный поток Ф, пронизывающий контур согласно теории электромагнетизма можно вычислить при помощи формулы:
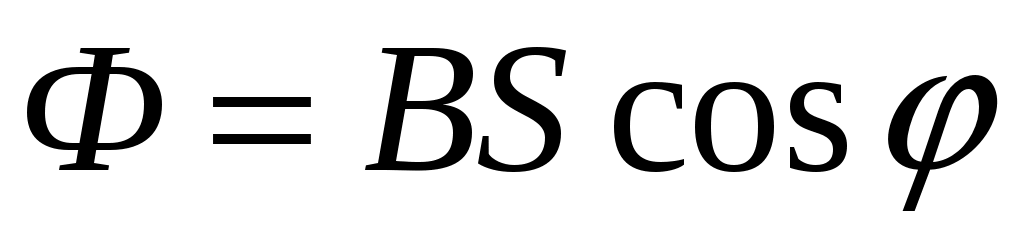
Поскольку все величины, которые входят в формулу, нам известны, то можно вычислить величину магнитного потока:
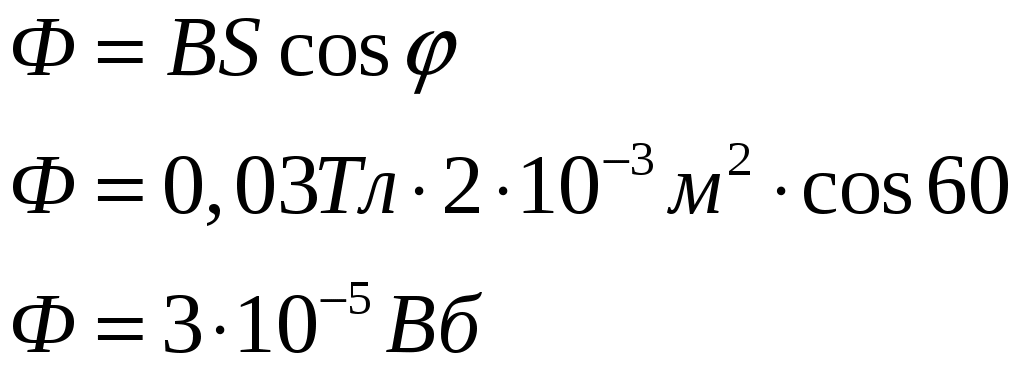
|
Ответ: 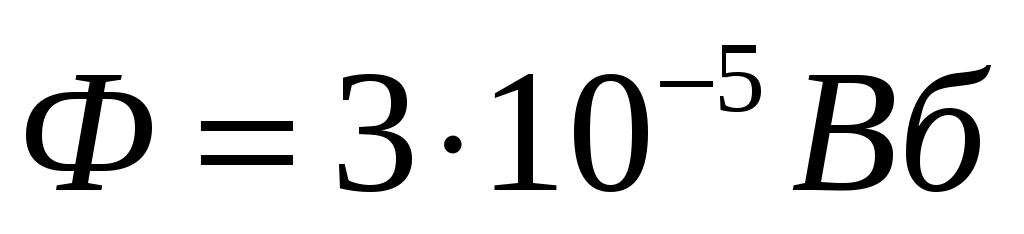 . .
|
461. В однородном магнитном поле (В = 0,1 Тл) равномерно с частотой n = 5 c-1 вращается стержень длиной l=50 см так, что плоскость его вращения перпендикулярна линиям напряженности, а ось вращения проходит через один из его концов. Определить индуцируемую на концах стержня разность потенциалов U.
Решение.
Дано:
В = 0,1 Тл
n = 5 c-1
l= 0,5 м
U - ?
|
Поскольку стержень вращается в переменном магнитном полу, то на его концах будет индуцироваться ЭДС. Величину этой ЭДС можно вычислить при помощи формулы:
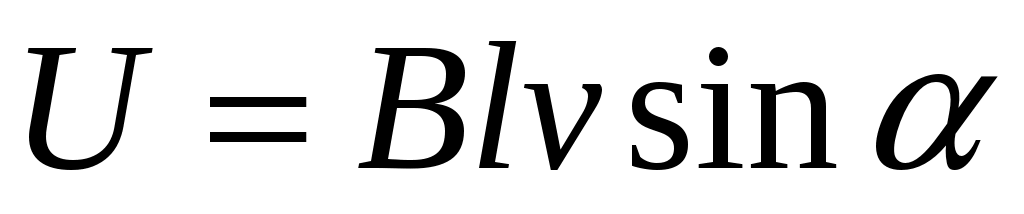
Поскольку 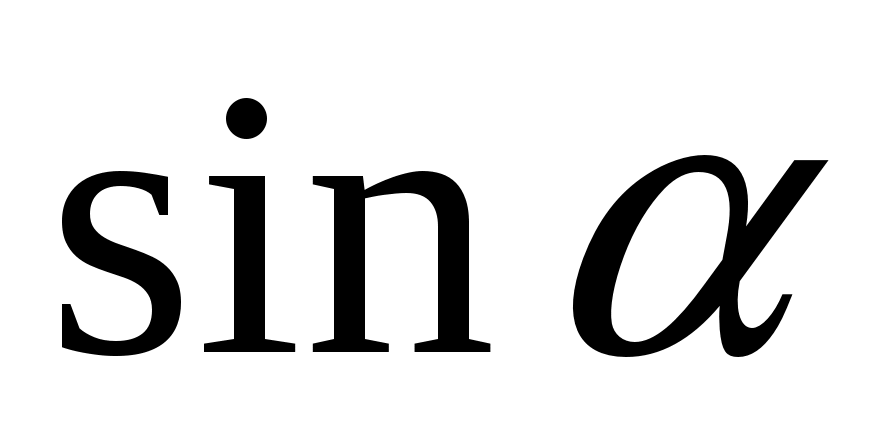 =1, то: =1, то:
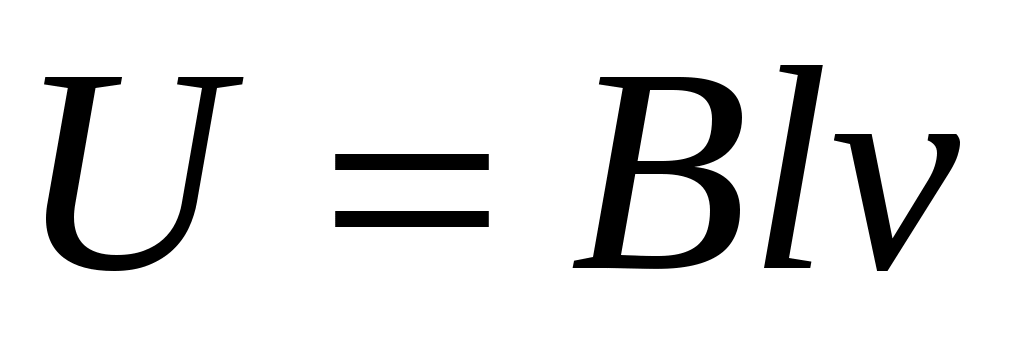
Скорость вращения стержня будет равна:
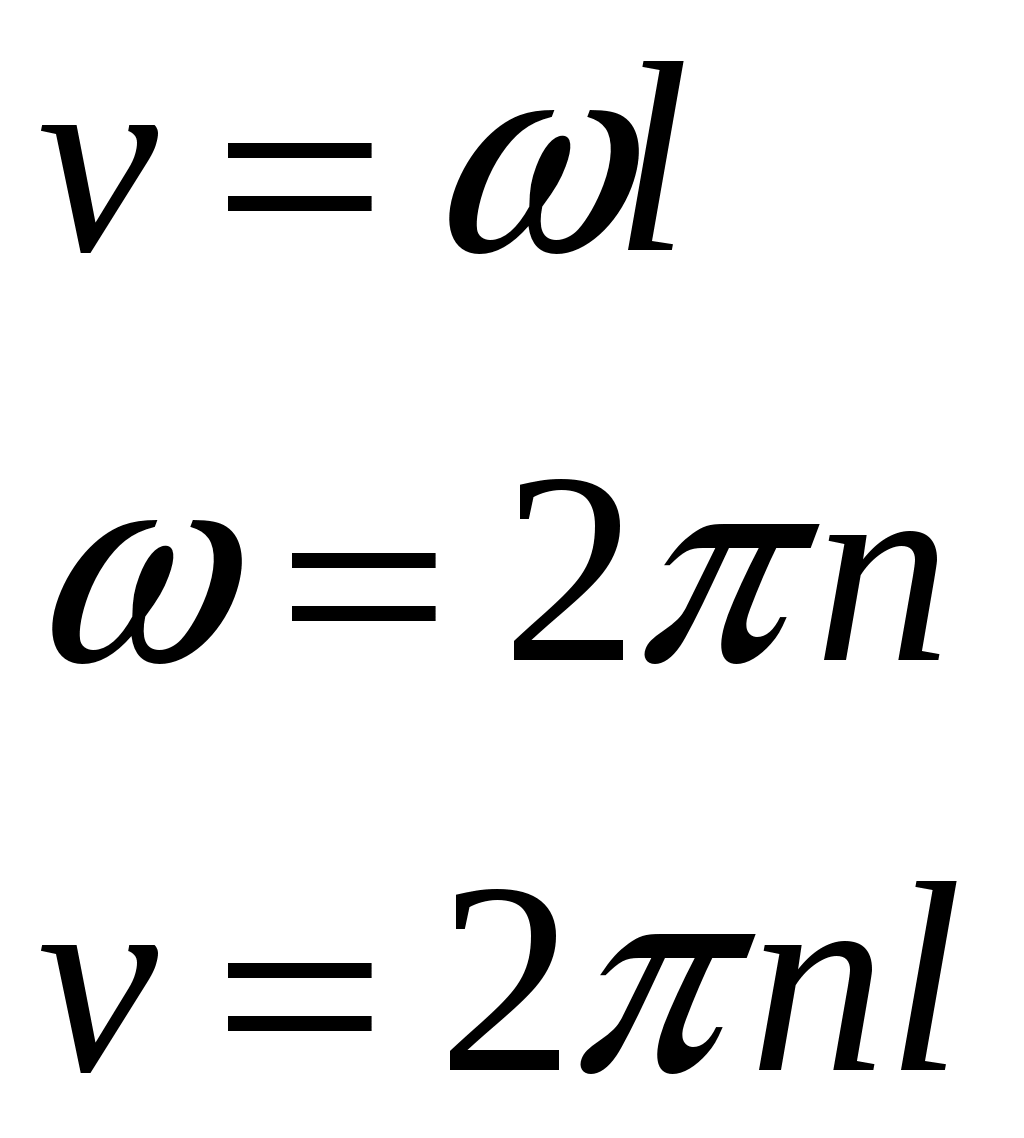
Тогда напряжение на концах стержня будет равно величине:
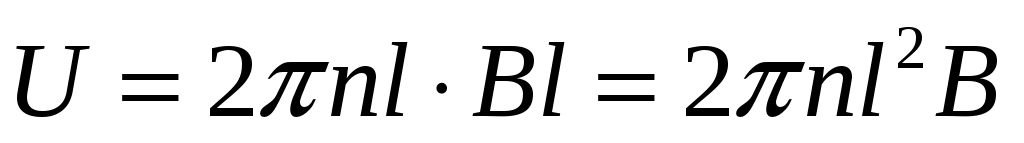
Подставим числовые данные в полученную формулу:
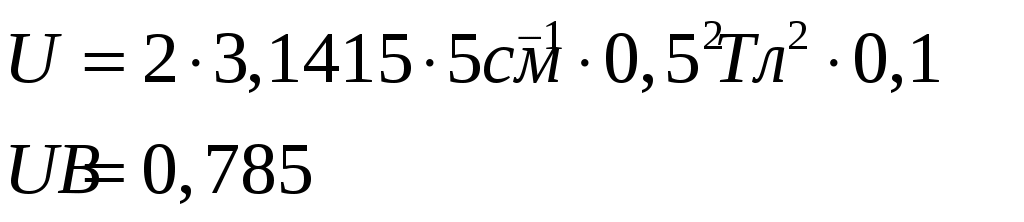
Напряжение на концах стержня равно 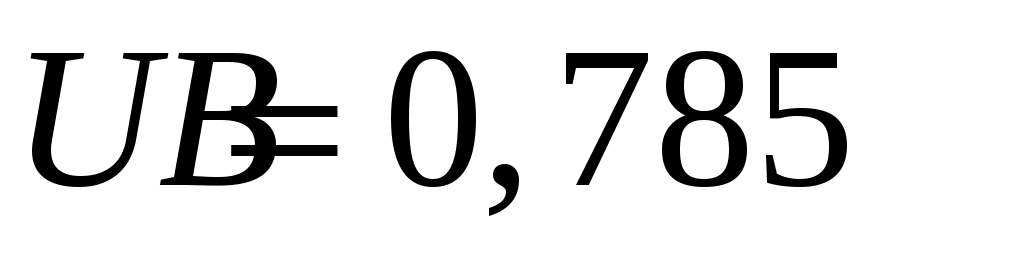 . .
|
Ответ: 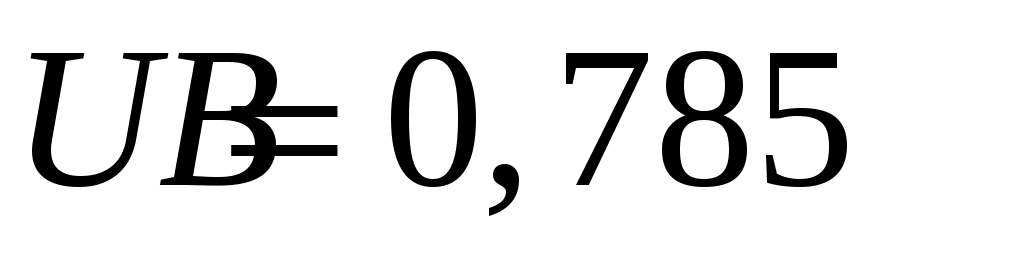
|
Список использованной литературы.
Дущенко В. П., Кучерук И. М. Общая физика. – К.: Высшая школа, 1995. – 430 с.
Зисман Г. А., Тодес О. М. Курс общей физики. В 3 т. – М.: Наука, 1995. – 343 с.
Кухлинг Х. Справочник по физике: Пер. с нем. – М.: Мир, 1983. – 520 с.
Яворский Б. М., Детлаф А. А. Справочник по физике. – М.: Наука, 1982. – 846 с.
Шебалин О. Д. Физические основы механики и акустики. – М.: Высшая школа, 1981. – 263 с.
|
|
|
 Скачать 231.5 Kb.
Скачать 231.5 Kb.

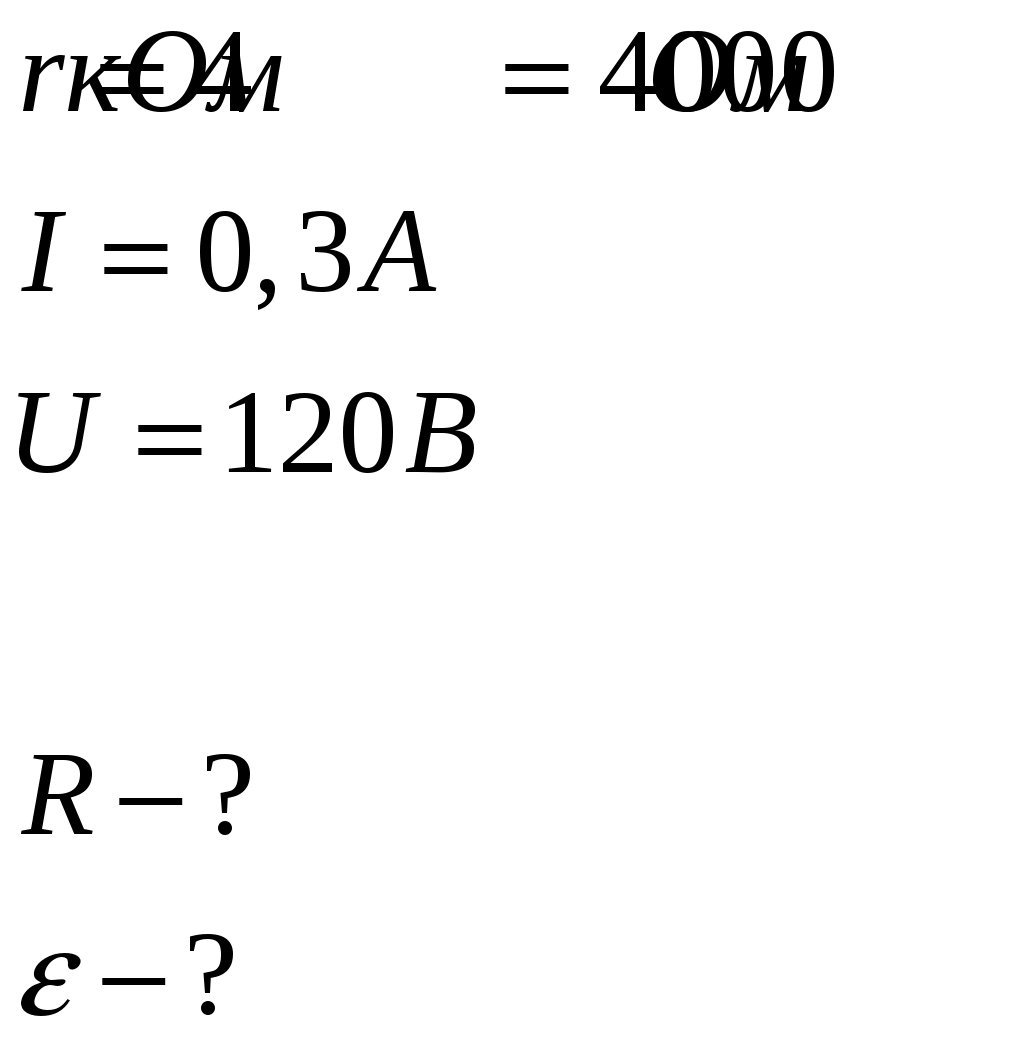
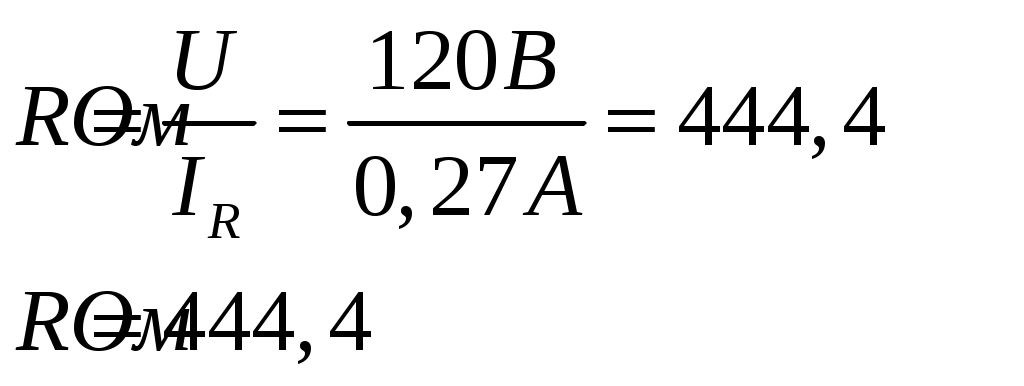
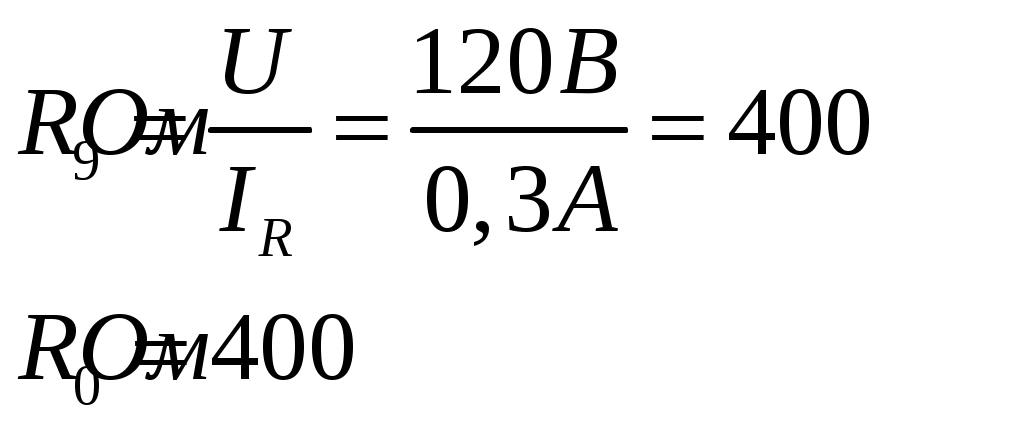
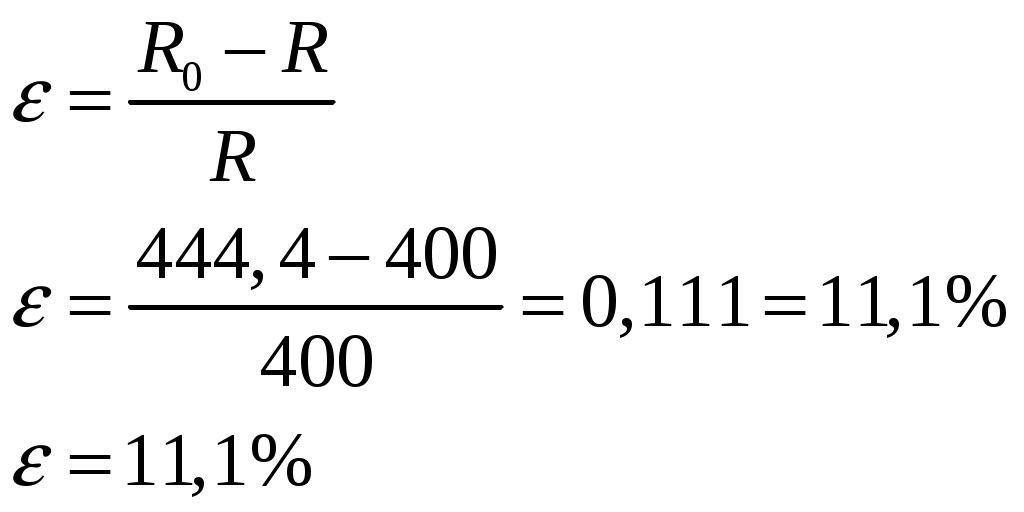
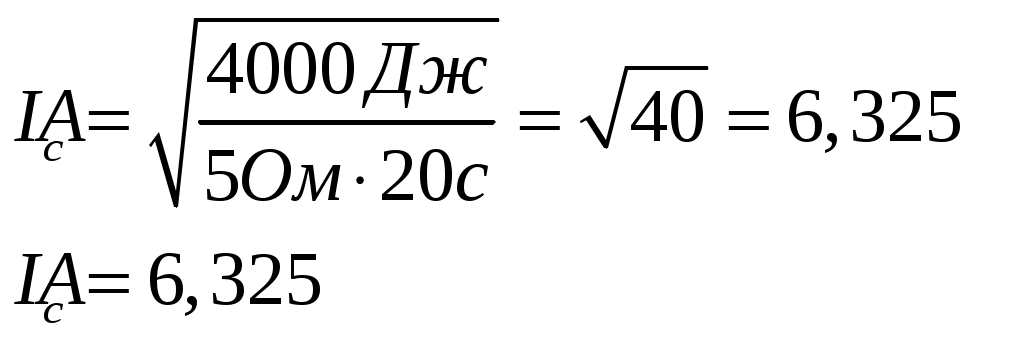
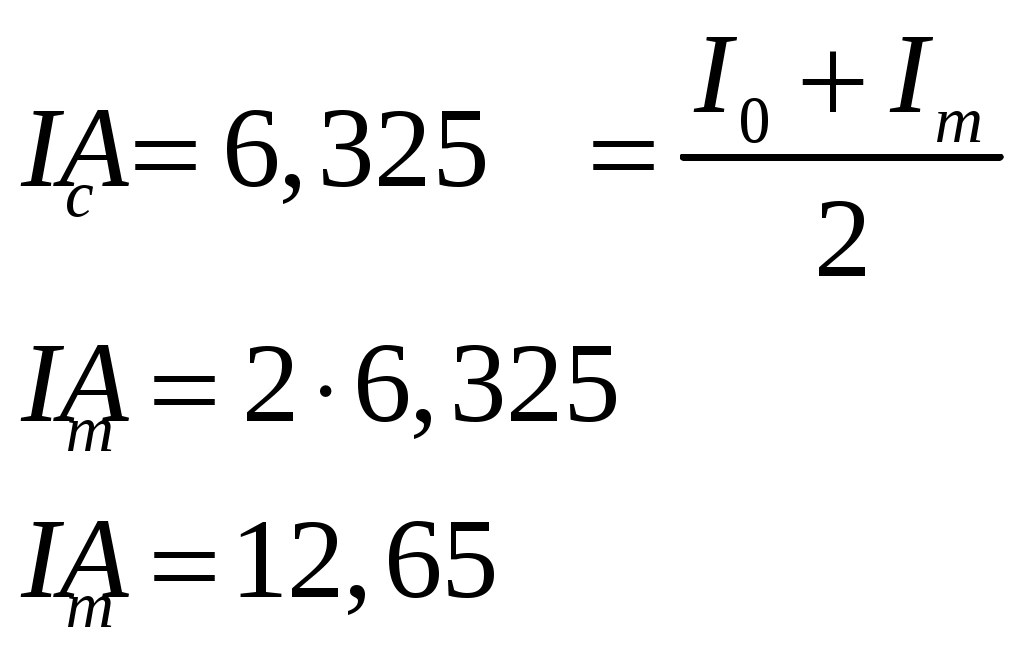
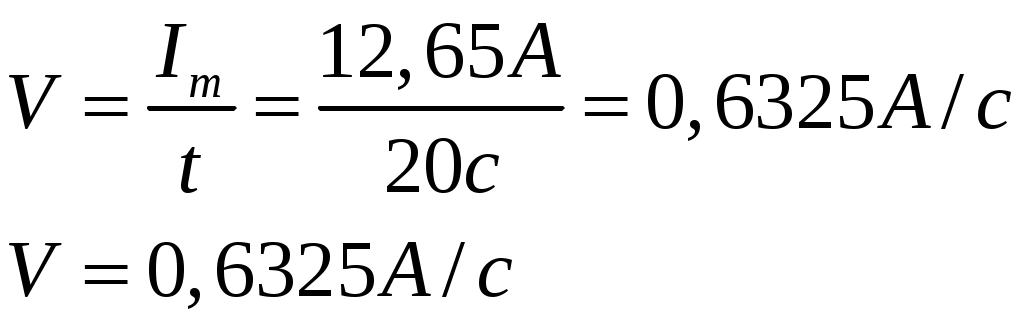
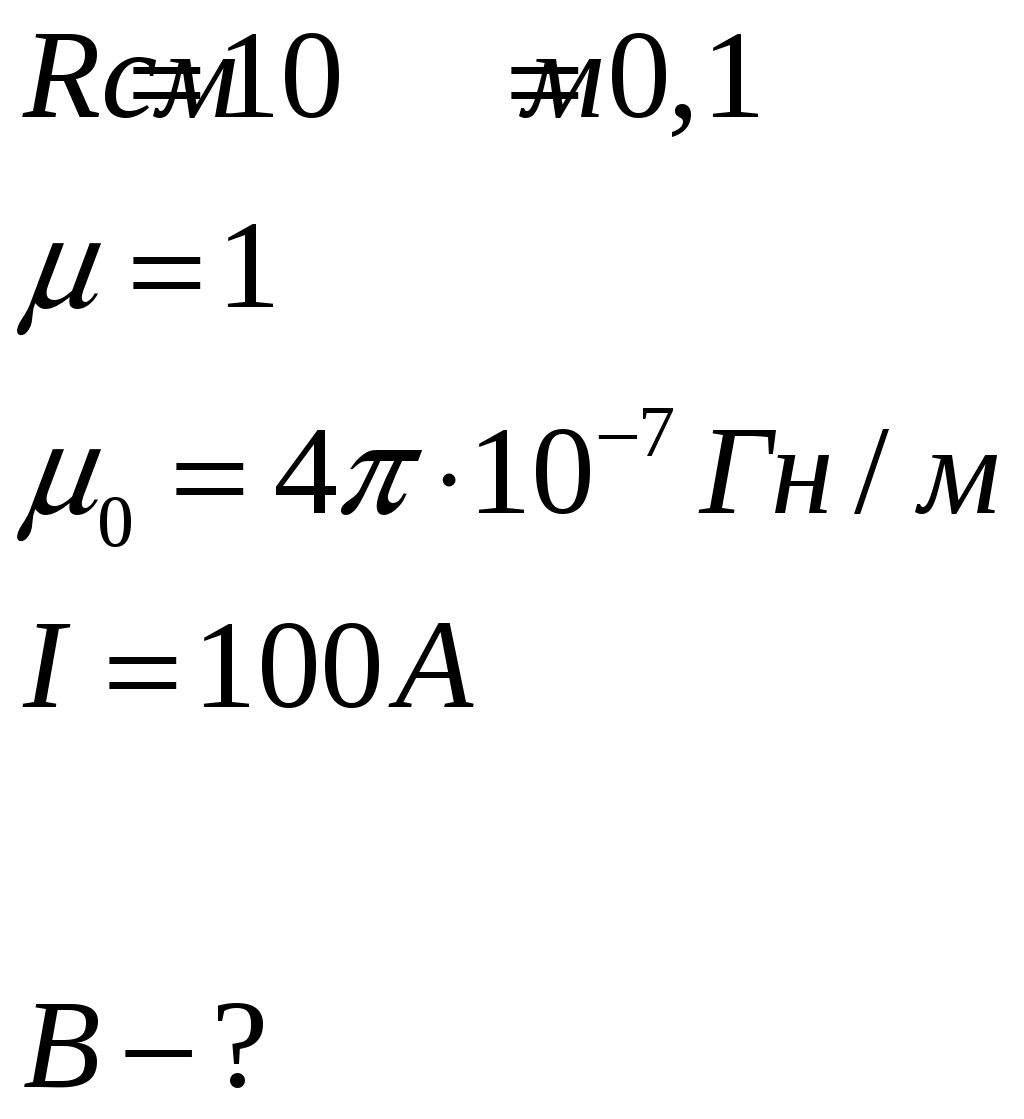
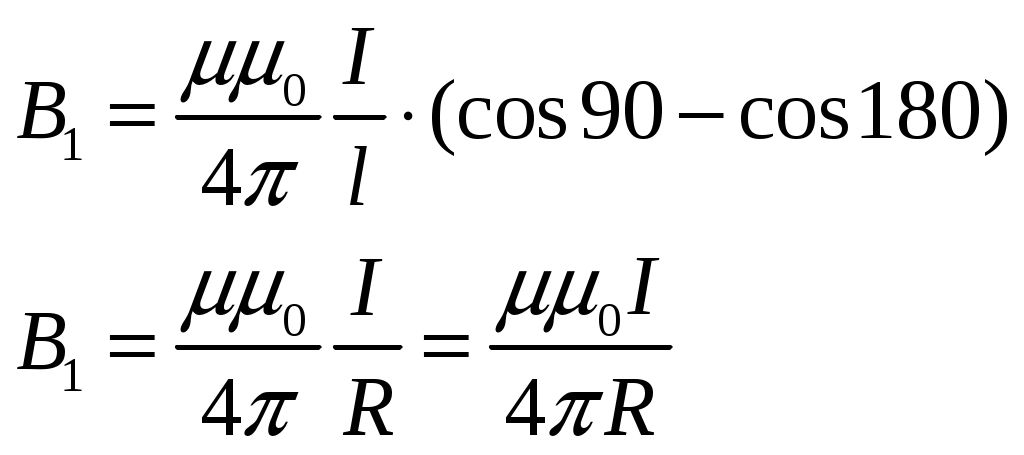
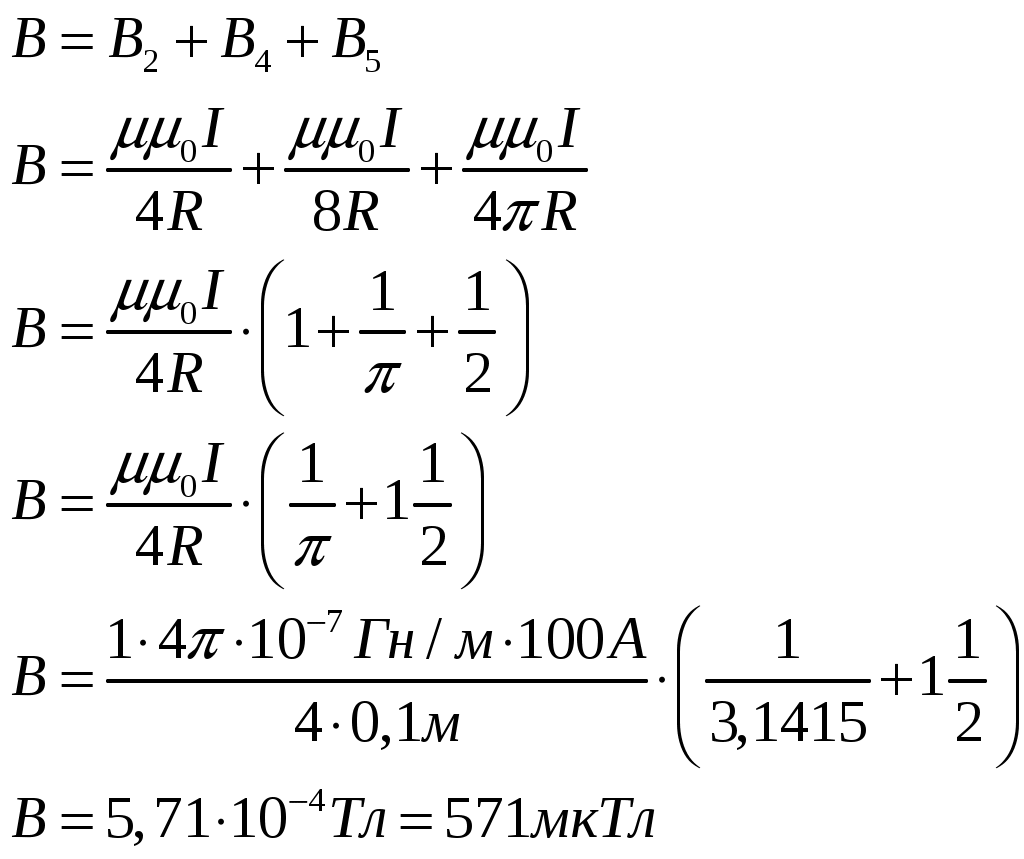
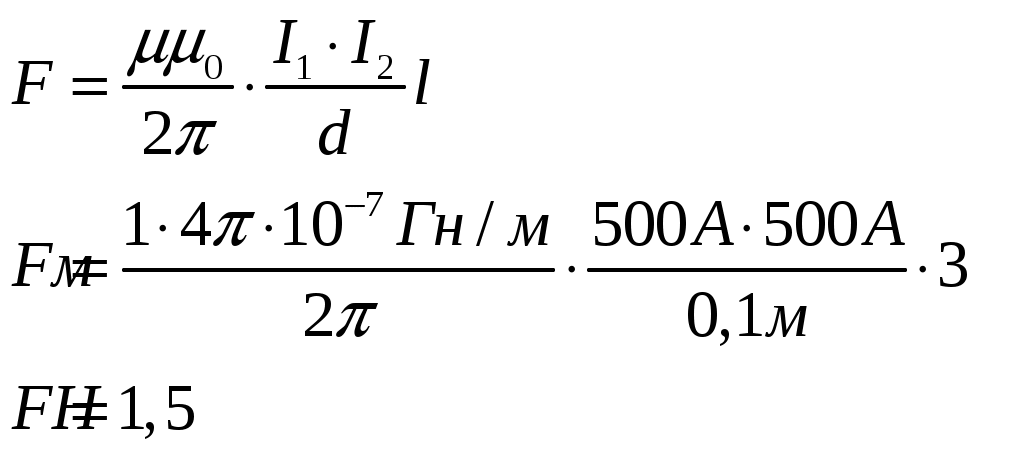
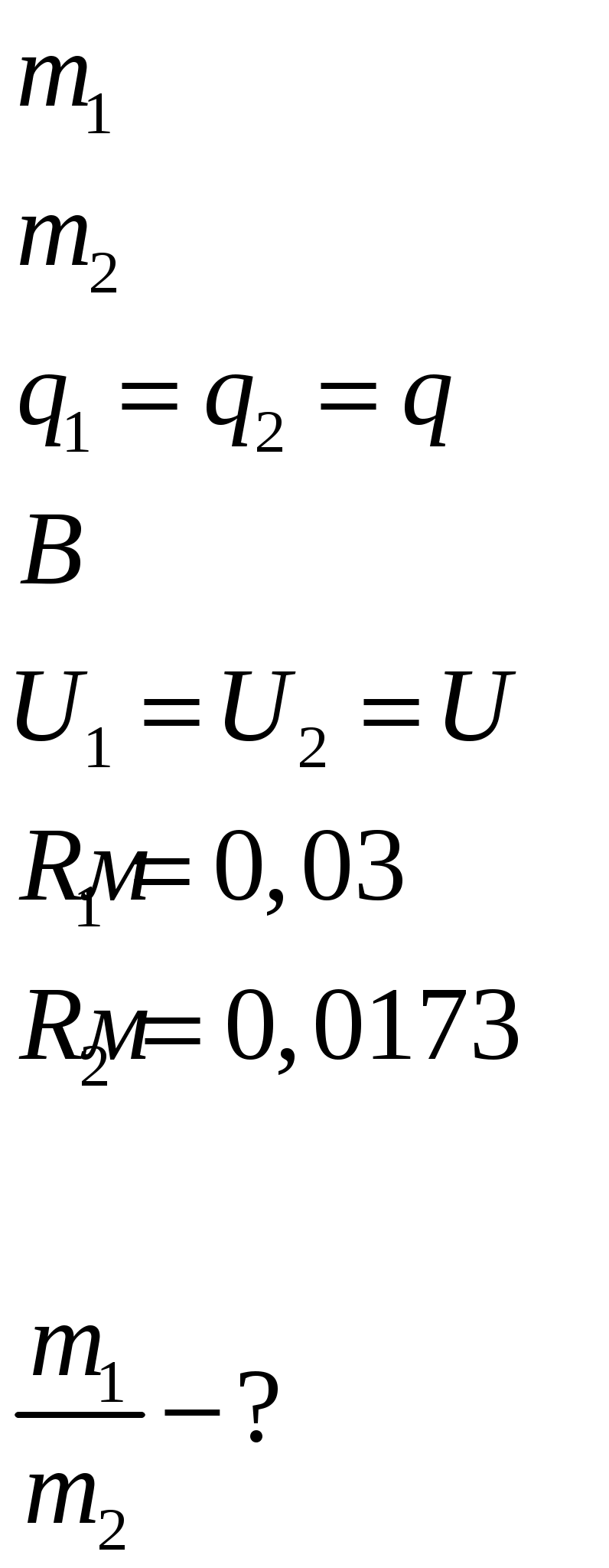
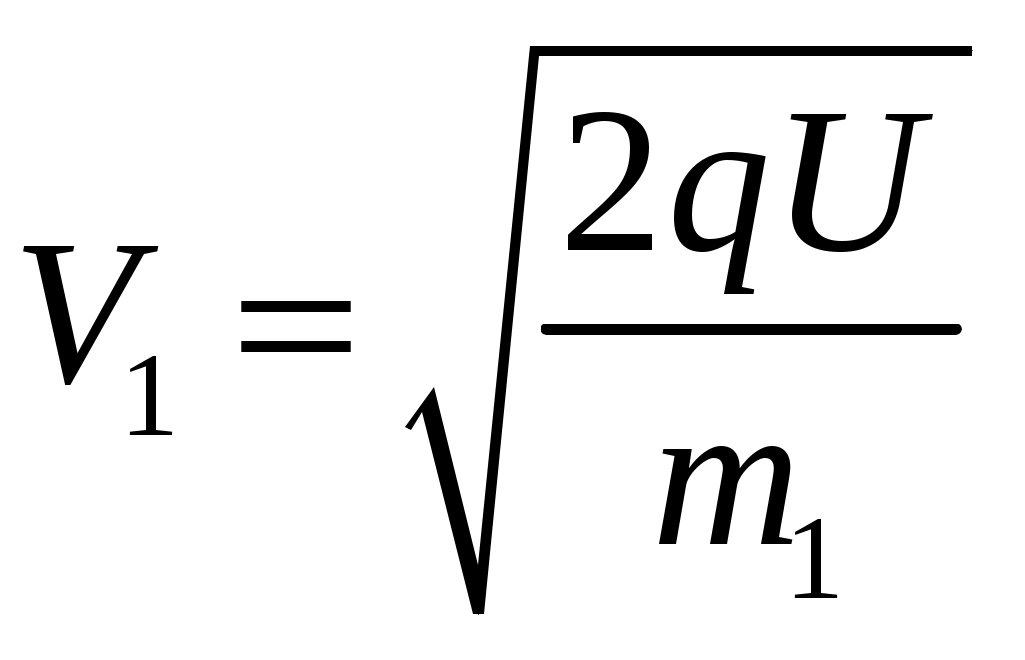 и
и 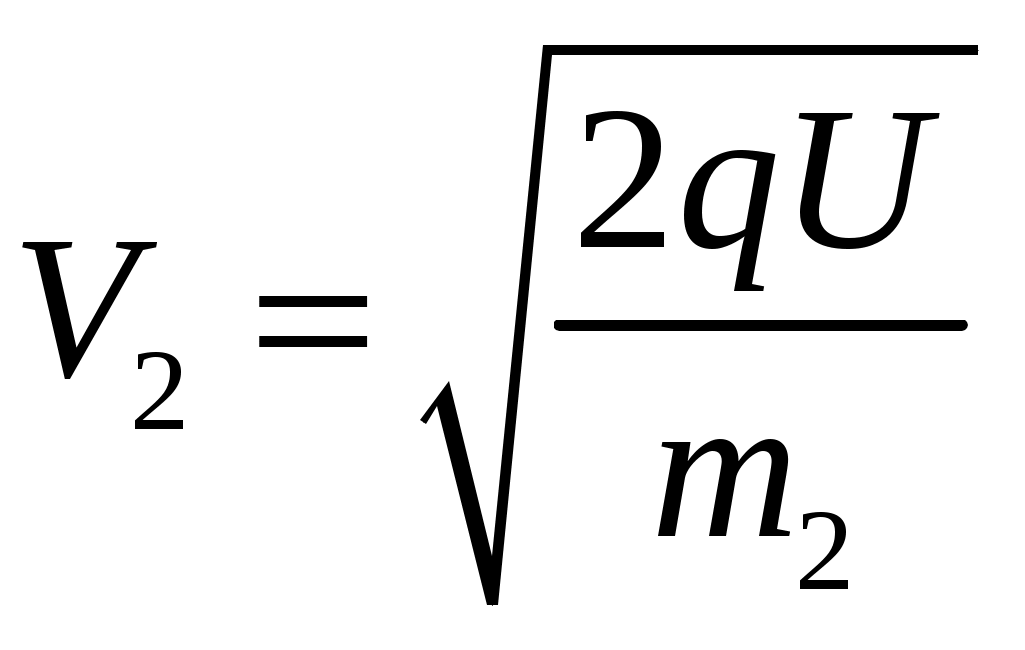 .
.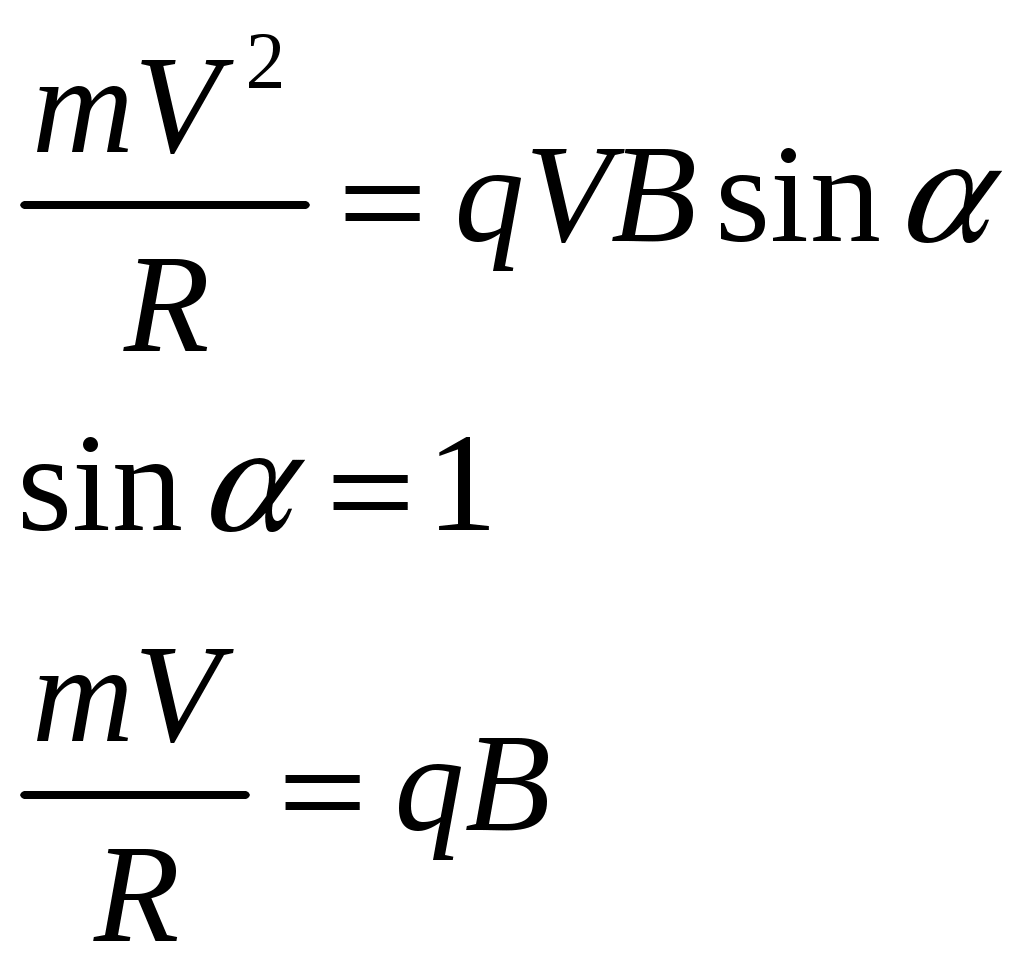
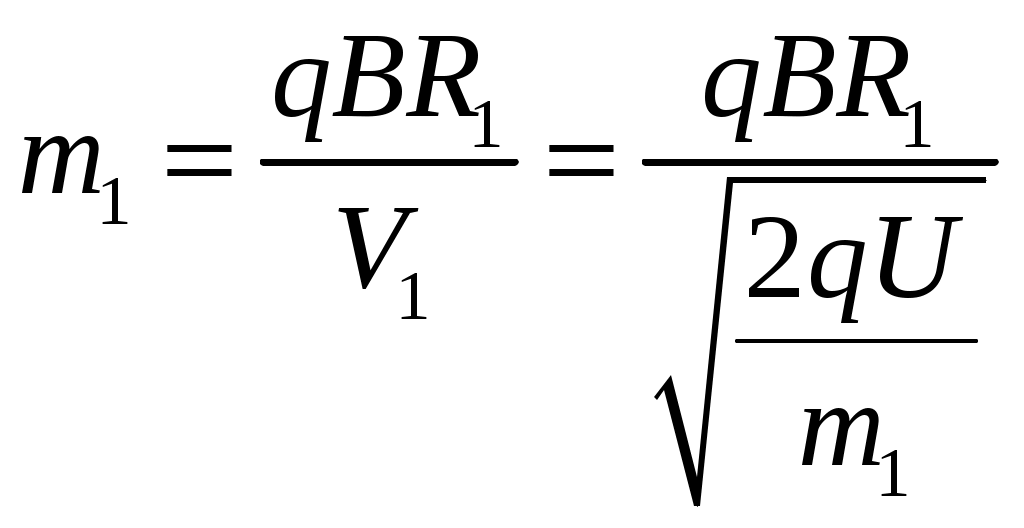 и для второй
и для второй 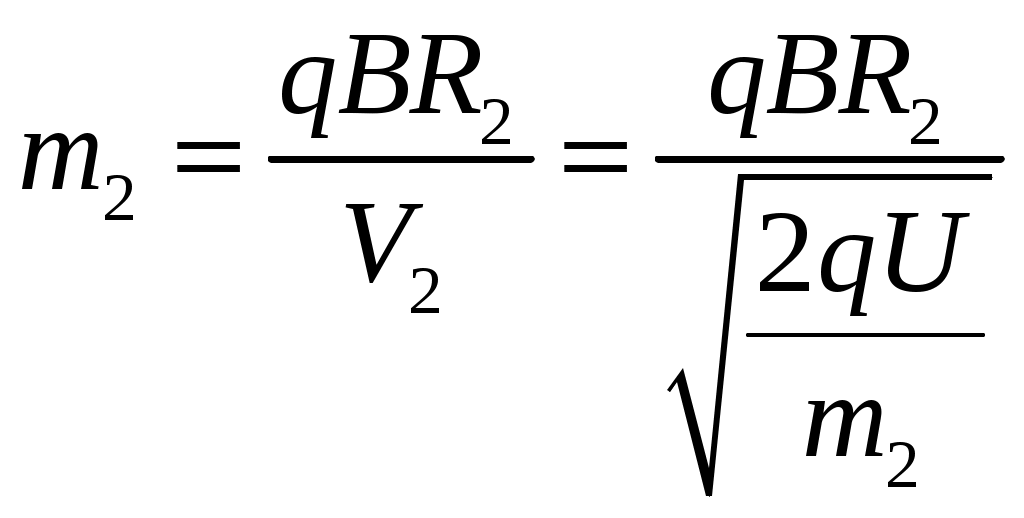 .
.