Монте Карло метод. Монте-Карло. Решение дифференциальных, интегральных и линейных алгебраических уравнений методом МонтеКарло

• Название: Решение дифференциальных, интегральных и линейных алгебраических уравнений методом МонтеКарло
• Анкор: Монте Карло метод
• Дата: 03.11.2022
• Размер: 121.06 Kb.
• Имя файла: Монте-Карло.doc
• Тип: Решение; #769351

СОДЕРЖАНИЕ
Введение………………………………………………………………………….…. 3

1. 
   Применение метода Монте-Карло в численном анализе ………………...... 4
   
2. 
   Понятие вычислительного эксперимента……………………………………5
   
3. 
   Метод Монте-Карло и его применение к приближенному вычислению интегралов………………………………………………………………………...….7
   
4. 
   Метод понижения дисперсии при вычислении интегралов: выделение главной части, метод существенной выборки, метод расслоения выборки………8
   
5. 
   Решение дифференциальных, интегральных и линейных алгебраических уравнений методом Монте-Карло………………………………………………..….9
   

Заключение ………………………………………………………………………... 11

Список литературы …………………………………………….………….………. 12

Введение

Одним из широко используемых подходов к численному моделированию физических систем является метод Монте-Карло, для применения которого необходим анализ большого количества случайных состояний и вариантов поведения исследуемой системы, что связано с большими объёмами вычислений.

Варианты случайного поведения системы, рассматриваемые методом Монте-Карло, обычно генерируются и обрабатываются по одному и тому же общему алгоритму, будучи при этом независимыми друг от друга. Это позволяет эффективно реализовывать метод Монте-Карло на поточно-парал­лельных вычислительных системах.

В последние годы появилась практическая возможность проведения поточно-параллельного физико-математического моделирования на графических процессорах (GPU) – вычислительных устройствах параллель­ной архитектуры, изначально предназначенных для отображения графики на персональных компьютерах и рабочих станциях.

В настоящее время ведущие производители графических процессоров сами позиционируют новые GPU как универсальные системы, предназначенные не только для графических вычислений, но и для расчётов общего назначения. В частности, компанией NVIDIA выпускаются графические процессоры архитектуры CUDA и соответствующее программное обеспечение, позволяющие сравнительно легко программировать GPU на языке, являющемся расширением языка C, сохраняющем синтаксис последнего и включающем все его основные возможности.

Современные графические процессоры имеют в своём составе до нескольких сотен параллельных процессоров, каждый из которых по вычислительной производительности сравним с центральным процессором персонального компьютера.

Результаты многих авторов показывают, что при решении хорошо распараллеливаемых задач реальная производительность GPU оказывается не менее чем на два порядка выше, чем у современных центральных процессоров ПК. Отметим, что затраты на приобретение и эксплуатацию одного вычислительного комплекса с GPU примерно совпадают с затратами на обычный персональный компьютер, тогда как кластер эквивалентной производительности занимал бы намного больше места, будучи при этом намного сложнее в эксплуатации и на порядки дороже.

1. 
   Применение метода Монте-Карло в численном анализе
   

Метод Монте-Карло применяется для исследования сложных систем. Принцип работы данного метода заключается в многократной имитации рассматриваемого процесса. Многократная имитация способствует получению большого набора данных определенных реализаций этого процесса. После этого набор данных проходит обработку расчета характеристик процесса.

Основная задача моделирования методом Монте-Карло — это анализ влияния неопределенности на системы при большом наборе ситуаций. Также метод служит для оценивания возможных результатов и их частоты для количественных величин. Актуальность метода Монте-Карло заключается в том, что он часто является единственным способом решения для многомерных задач, тогда как аналитические методы возможно использовать только для задач меньшей размерности.

Идея метода состоит в следующем:

- определяется модель, которая лучше всего отражает поведение изучаемой системы;

- данная модель тестируется множество раз с использованием случайных чисел для вывода выходных данных модели;

- модель многократно запускается на компьютере в каждом полученном случае с различными входными данными для вывода набора результатов.

Применение случайных равномерно распределенных чисел (СРРЧ) является основой метода Монте-Карло. Розыгрыш СРРЧ производится с помощью специальных алгоритмов, благодаря которым рассчитывается бесконечная последовательность чисел. При этом значения СРРЧ всегда попадают в диапазон от нуля до единицы. СРРЧ имеют 3 свойства: равномерность, независимость и случайность.

Свойство равномерности заключается в том, что СРРЧ принимают значения от 0 до 1 с одинаковой частотой; независимости – все значения СРРЧ не зависят от любых предыдущих; случайности – последовательность СРРЧ не имеет какой-либо закономерности.

Один из алгоритмов получения СРРЧ – алгоритм Лемера. Для данного алгоритма задается три параметра: равномерность (𝑅0), случайность (𝑎) и независимость (𝑚). Значения параметров подбираются при отладке алгоритма.

Процедура реализации розыгрыша СРРЧ на основе алгоритма Лемера:

1. Вычисляется произведение 𝑎𝑅𝑛−1, где 𝑛 – номер разыгрываемого СРРЧ.

2. Рассчитывается величина 𝑅𝑛 как остаток от деления числа на параметр 𝑚: 𝑅𝑛 = 𝑚𝑜𝑑(𝑎𝑅𝑛−1/𝑚), (1) где 𝑚𝑜𝑑 – остаток от деления.

3. Находится СРРЧ по формуле: 𝑅 = 𝑅𝑛 𝑚.

Пример розыгрыша трех СРРЧ на основе алгоритма Лемера, где𝑎 = 5, 𝑚 = 9, 𝑅0 = 3.

Розыгрыш 1. Вычисляется произведение 𝑎𝑅𝑛−1 = 𝑎𝑅0 = 5·3 = 15. Рассчитывается величина 𝑅𝑛: 𝑅𝑛 = 𝑅1 = 𝑚𝑜𝑑(15/9) = 6. Находится СРРЧ: 𝑅 = 6/9 = 0,6666.

Розыгрыш 2. Вычисляется произведение 𝑎𝑅𝑛−1 = 𝑎𝑅1 = 5·6 = 30 (здесь 𝑅𝑛−1 = 𝑅1 = 6 было вычислено в предыдущем розыгрыше). Рассчитывается величина 𝑅𝑛: 𝑅𝑛 = 𝑅2 = 𝑚𝑜𝑑(30/9) = 3. Находится СРРЧ: 𝑅 = 3/9 = 0,3333.

Розыгрыш 3. Вычисляется произведение 𝑎𝑅𝑛−1 = 𝑎𝑅2 = 5·3 = 15. Рассчитывается величина 𝑅𝑛: 𝑅𝑛 = 𝑅3 = 𝑚𝑜𝑑(15/9) = 6. Находится СРРЧ: 𝑅 = 6/9 = 0,6666.

Алгоритм решения основан на имитации случайных событий. Имитация случайного события на основе метода Монте-Карло представляет следующее. Разыгрывается СРРЧ R, если 0 ≤ 𝑅 < 𝑃, где P – вероятность имитируемого события, то моделируется появление данного события; если 𝑅 ≥ 𝑃, то моделируется отсутствие события.

2. 
   Понятие вычислительного эксперимента
   

В широком (методологическом) смысле под вычислительным экспериментом мы понимаем новую технологию научных исследований.

Для исследуемого объекта сначала строится математическая модель. Она базируется на известных фундаментальных моделях.

Вычислительный эксперимент, по своей сути, предусматривает исследование группы близких моделей. Вначале строится простая, но достаточно содержательная и полная с точки зрения описания исследуемых процессов и близости к экспериментальным данным модель. В процессе проведения вычислительного эксперимента, на его последующих циклах модель уточняется, учитываются новые факторы и т.д.

Поэтому мы всегда можем говорить (более того, должны говорить) о наборе, упорядоченном наборе (об иерархии) математических моделей, каждая из которых с той или иной точностью описывает действительность. И в рамках наиболее простой модели необходимо добиваться согласия с экспериментом. Это и является, в конце концов, целью вычислительного эксперимента.

Суть вычислительного эксперимента, его содержательное зерно состоит в исследовании на компьютере математических моделей численными методами.

Основное содержание предварительного исследования математической модели состоит в выделении более простых (модельных) задач и их всестороннем исследовании, так как полная математическая модель слишком сложна.

Модельные математические задачи в цикле вычислительного эксперимента строятся для двух различных целей: во-первых, для качественного исследования полной задачи (а опосредованно и исследуемого объекта), во-вторых – для проверки, тестирования вычислительных алгоритмов приближенного решения полной задачи.

В вычислительном эксперименте проблемы хранения и обработки информации имеют все возрастающее значение. На этапе анализа результатов становиться ясным, удачно ли выбрана математическая модель, ее вычислительная реализация. Если есть необходимость, модели и численные методы уточняются, и весь цикл вычислительного эксперимента повторяется, то есть совершается новый виток спирали в познании истины.

Основные особенности новой технологии научных исследований чрезвычайно важно отметить универсальность вычислительного эксперимента, которая позволяет легко переносить эту технологию на исследование других объектов. Это обстоятельство порождено тем, что многие явления и процессы имеют одни и те же математические модели.

Второй особенностью вычислительного эксперимента как технологии научных исследований является его междисциплинарный характер.

Математическое моделирование традиционно развивается в недрах фундаментальных наук: механике и физике, для которых отмечается наивысший уровень теоретических исследований (другими словами, уровень математизации). Значительно менее совершенен математический арсенал инженера и технолога. В современных условиях необходимо обеспечить повсеместное непосредственное внедрение математических методов в науку и технологию.

Наиболее благодатное поле для приложения методов математического моделирования и вычислительного эксперимента – техника и промышленность, технология. Особое внимание заслуживают отрасли, определяющие научно-технический прогресс сегодня, и прежде всего микроэлектроника и нанотехнологии. В настоящее время мировая общественность совершенно справедливо обеспокоена экологическими последствиями крупномасштабных проектов, обеспечением безопасности функционирования работающих установок и проектируемых объектов. Вычислительный эксперимент на базе адекватных моделей позволяет испытать модель экологически опасного объекта в мыслимых и немыслимых условиях, дать практические рекомендации обеспечения условий безопасной работы, дать, если хотите, гарантии такой работы.

При исследовании нового процесса или явления обычный подход связан с построением математической модели и проведением расчетов при изменении параметров задачи. В этом случае мы имеем поисковый вычислительный эксперимент.

В результате проведения поискового вычислительного эксперимента дается описание наблюдаемым явлениям, прогнозируется поведение исследуемого объекта в тех или иных условиях, возможно и не достижимых в реальных условиях. Такой тип вычислительного эксперимента характерен при проведении теоретических исследований в фундаментальных науках.

С другой стороны, при математическом моделировании технологических процессов в качестве основного может быть выбран оптимизационный вычислительный эксперимент. Для него характерно решение задачи оптимизации по уменьшению затрат, облегчению конструкции и т.д.

Для сформулированной математической модели ставится соответствующая задача оптимального управления, задача оптимизации. При обработке данных натурных экспериментов используется диагностический вычислительный эксперимент. По дополнительным косвенным измерениям делается вывод о внутренних связях явления или процесса.

3. 
   Метод Монте-Карло и его применение к приближенному вычислению интегралов
   

Основные вероятностные характеристики непрерывной случайной величины x определяются интегралами, связанными с её п. р. в. f(t). К их числу относятся следующие характеристики:
- вероятность попадания x в интервал (a,b)

- математическое ожидание x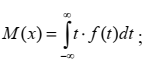



- математическое ожидание любой функции φ от случайной величины x



- математическое ожидание x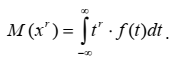



Часто эти интегралы сложны для вычисления. При статистическом моделировании вместо точных значений можно вычислять и использовать соответствующие приближённые эмпирические оценки, легко рассчитываемые по выборке x1, x2, …, xn:

- оценку вероятности попадания x в интервал (a,b), где функция I [A] – индикатор события A – равна 1, когда событие A имеет место, и равна нулю в противном случае;

- оценку математического ожидания x;

- оценку математического ожидания любой функции φ(x) от случайной величины x;

- оценку математического ожидания xr (r-го начального момента).

Оценки легко вычисляются, и погрешности, с которыми они
приближают точные значения характеристик, легко контролируются. Действительно, как суммы большого числа независимых случайных величин они имеют нормальное распределение. При этом математическое ожидание оценок характеристик совпадают с точными значениями характеристик, а фактические отклонения оценок от точных значений характеристик подчиняются известному правилу «трёх сигм» и могут быть сделаны сколь угодно малыми путём увеличения объёма выборки n.

Основная идея метода Монте-Карло состоит в том, чтобы использовать
расчёт эмпирических оценок в качестве способа вычисления определённых интегралов вида.

Поскольку к такому виду легко сводятся практически любые определённые интегралы, метод Монте-Карло оказывается достаточно универсальным методом. Преимущества метода Монте-Карло и условия, в которых они проявляются, можно увидеть, рассмотрев некоторые примеры его применения.

4. 
   Метод понижения дисперсии при вычислении интегралов: выделение главной части, метод существенной выборки, метод расслоения выборки
   

Количество испытаний, необходимое для вычисления интеграла с заданной точностью, зависит, как было показано выше, от дисперсии соответствующей случайной величины. Существуют различные приемы преобразования задачи, позволяющие уменьшать дисперсию и, следовательно, время вычислений. Если часть задачи можно решить аналитически, то, используя это частичное решение, обычно удается построить метод Монте-Карло для решения всей задачи с меньшей дисперсией. Правда, вообще говоря, построенные таким путем методы могут оказаться более трудоемкими и в конечном счете невыгодными.

Выделение главной части.

Если главную часть задачи можно вычислить аналитически, то, как правило, выгодно считать методом Монте-Карло не всю задачу, а только «поправку» — разницу между всей задачей и главной частью. Уменьшение дисперсии при этом может оказаться очень значительным.

Метод существенной выборки.

Этот метод устроен так, что большинство точек выбирается в той части области интегрирования Q, которая дает наибольший вклад в интеграл, что достигается специальным выбором вспомогательной плотности f(pr). Метод существенной выборки аналогичен по идее одноименному методу при моделировании случайных величин методом отбора. В обоих случаях надо удачно выбрать вспомогательную плотность. При моделировании такой выбор обеспечивает высокую эффективность отбора на втором шаге алгоритма. При вычислении интегралов удачный выбор вспомогательной плотности минимизирует дисперсию осредняемой случайной величины.

Метод расслоения выборки.

Допустим, что мы умеем (аналитически) вычислить интегралы по некоторой части области G. Тогда выгодно представить интеграл в виде суммы интегралов по областям B и G − B, и методом Монте-Карло вычислить только интеграл по области G − B. Чем область B больше, тем заметнее будет понижение дисперсии.

Если аналитически взять интеграл по некоторым из переменных, а по остальным переменным использовать тот же метод Монте-Карло, то дисперсия уменьшится. Правда, нередко бывает, что после интегрирования по некоторым из переменных получаются более сложные формулы счета и, несмотря на уменьшение дисперсии, трудоемкость возрастает.

5. 
   Решение дифференциальных, интегральных и линейных алгебраических уравнений методом Монте-Карло
   

Метод Монте-Карло для решения систем дифференциальных, интегральных и линейных алгебраических уравнений рекомендуется использовать в том случае, если ее порядок достаточно велик. В монографиях с помощью метода Монте-Карло вычисляется одна компонента вектора решения или скалярное произведение вектора решения и произвольного вектора. Представлены алгоритмы Монте-Карло, позволяющие получать итерационное решение системы линейных уравнений при условиях более слабых, чем условия обычного метода Монте-Карло.

Особенность построения случайного вектора заключается в том, что математическое ожидание очередной итерации совпадает с итерацией Зейделя.

Рассмотрим метод, применимый к решению системы линейных алгебраических уравнений общего вида: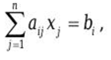



где i = 1, ..., п.

Решение системы равносильно минимизации квадратичной формы: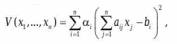




где ai, (Х2, ..., а„ - некоторые положительные константы.

Определим n-мерный эллипсоид



 

Пусть х = (х].....Х„) - вектор решения системы уравнений, тогда очевидно, что вектор X является центром симметрии эллипсоида. Это означает, что каждая из иперплоскостей X , = X ., проходящая через центр эллипсоида, делит его объем пополам. По этой причине решение системы сводится к нахождению таких значений X,,..., Х„, что объемы частей эллипсоида, лежащих в полупространствах Xj < Х_; и Xj > х), совпадают и равняются половине объема эллипсоида.

Обычно решение во многих случаях даже этой простейшей задачи является весьма трудоемким. Это связано в первую очередь с тем, что часто приходится использовать итерационные способы (если невыгодно применять так называемый метод прогонки или факторизации). При итерационных способах решения нужно многократно использовать значения неизвестной функции и во всех узлах решетки. Так как количество узлов обычно очень велико, то это вызывает трудности при хранении значений функции и в оперативной памяти машины и требует большого количества обращений к внешней памяти. Таким образом, происходит большая потеря машинного времени.

Таким образом, переход к многомерным задачам очень быстро выводит за пределы возможностей машинной памяти (оперативной и внешней) современных универсальных цифровых машин.

Все эти соображения указывают, что разработка других методов решения краевых задач, свободных от указанных недостатков, является очень существенной.

Заключение

Метод Монте-Карло позволяет эффективно использовать параллельную архитектуру современных графических процессоров за счёт обработки альтернативных случайных вариантов поведения моделируемой системы в большом количестве независимых вычислительных потоков.

Преимущества метода Монте-Карло:

- связь между входными и выходными данными очевидна, что обеспечивает простоту понимания модели;

- применение данного метода возможно для любого распределения входной переменной;

- для определения сильных и слабых воздействий имеется возможность применения анализа чувствительности;

- при методе Монте-Карло во внимание могут приниматься любые условия, которые возникают в реальности;

- для реализации метода имеется доступное программное обеспечение.

Недостатки метода Монте-Карло:

- точность результата зависит от количества имитаций;

- основой метода является представление неопределенности параметров посредством достоверного распределения;

- для разработчиков моделей сложные структуры вызывают определенные трудности и усложняют взаимодействие с заинтересованными сторонами;

- данный метод плохо восприимчив к маловероятным событиям, что влечет к серьезным последствиям.

На развитие вычислительной математики метод Монте-Карло оказывает значительное влияние. Сочетание данного метода с другими вычислительными методами, а также дополнение их при решении задач является одной из его особенностей.

Применение данного метода присуще, прежде всего, задачам с теоретико-вероятностном описанием. Это способствует естественности получения ответа с заданной вероятностью в задачах и значительному упрощению процедуры решения.


СПИСОК ЛИТЕРАТУРЫ

1. 
   Боярченков, А.С., Поташников, С.И. Использование графических процессоров и технологии CUDA для задач молекулярной динамики // Вычислительные методы и программирование. 2009. № 10. С. 9–23. http://num-meth.srcc.msu.ru/zhurnal/tom_2009/v10r102.html.
   
2. 
   Ермаков, С. М. Метод Монте-Карло в вычислительной математике / С. М. Ермаков — Москва: Наука, 2008. — 192 с.
   
3. 
   Метод Монте-Карло на графических процессорах: учебное пособие для проведения практических занятий и самостоятельной работы / К.А. Некрасов, С.И. Поташников, А.С. Боярченков, А.Я. Купряжкин. Екатерин­бург: УГТУ-УПИ, 2009. 58 с.
   
4. 
   Поташников, С.И., Боярченков, А.С., Некрасов, К.А., Купряжкин, А.Я., Рисо­ваный, В.Д., Голованов, В.Н. Высокоскоростное моделирование диффузии ионов урана и кислорода в UO₂ // Сборник рефератов и докладов семинара «Во­просы создания новых методик исследований
   и испытаний, сличитель­ных экспериментов, аттестации и аккредита­ции» Димитровград, 22-23 ноября 2005 г. / НИИАР. Димитровград, 2007. С. 
   139–159.
   
5. 
   Поташников, С.И., Боярченков, А.С., Некрасов, К.А., Купряжкин, А.Я. Молеку­лярно-динамическое восстановление межчастичных потенциалов в диоксиде урана по тепловому расширению // Альтернативная энергетика и экология. 2007. № 8. С. 43–52.
   
6. 
   Савелова, Т. И. Метод Монте-Карло: учеб. пос. / Т. И. Савелова — Москва: НИЯУ МИФИ, 2011. — 152 с
   
7. 
   Смородинский, С. С. Оптимизация решений на основе компьютерных имитационных методов и моделей / С. С. Смородинский, Н. В. Батин — Минск: БГУИР, 2004. — 79 с.
   
8. 
   Соболь И.М. Метод Монте – Карло. / И.М. Соболь М.: Наука, 1985. 78 с.