Решение дифференциальных уравнений

• Название: Решение дифференциальных уравнений
• Дата: 11.11.2021
• Размер: 81.52 Kb.
• Имя файла: Laba_4_Slastin_Nikon.docx
• Тип: Решение; #269264

_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РАПС

отчет

по лабораторной работе №4

по дисциплине «Информатика»

Тема: Решение дифференциальных уравнений

Студент гр. 1487		Сластин Н.Ю.
Преподаватель		Пожидаев А. К.

Санкт-Петербург

2020

Цель работы.

Освоить технику работы с математическим пакетом MathCad.
Основные теоретические положения.

Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается лёгкостью использования и применения для коллективной работы.

Mathcad содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции со скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.
Ход работы.

Найти функцию у(х), удовлетворяющую дифференциальному уравнению

и имеющую значение 0 при x = 0.

Это простое дифференциальное уравнение допускает точное аналитическое решение, однако в данном упражнении предполагается использование стандартной функции программы MathCad, осуществляющей численное решение данного урав­нения. Результат вычислений можно после этого сравнить с точным решением.

4.1. Запускаем программу MathCad.

4.2. Зададим начальное значение функции как элемент вектора у, размерность которого соответствует числу решаемых уравнений: у₀:= 0.

4.3. Создаем функцию Т(х, у), которая вычисляет значение производной при задан­ных значениях независимой переменной и неизвестной функции:

T(x, y) := –y₀ + x∙cos(x).

4.4. Определяем начальное и конечное значение отрезка интегрирования.

a :=0, b := 12∙.

4.5. Указываем число шагов интегрирования К:=20.

4.6. Вычислили численное решение уравнения при помощи функции rkfixed.

Z:= rkfixed(y,a,b,K,T).

4.7. Построили график полученного решения.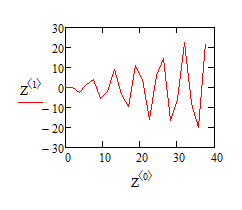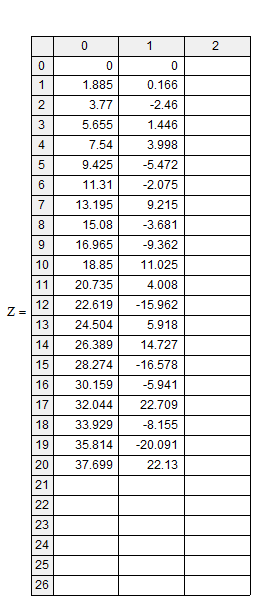



4.8. Измен. число шагов, на которые делится отрезок интегрирования, и иссле­дую, как изменяется результат расчета при уменьшении и увеличении этого параметра.

Изменили на K:=30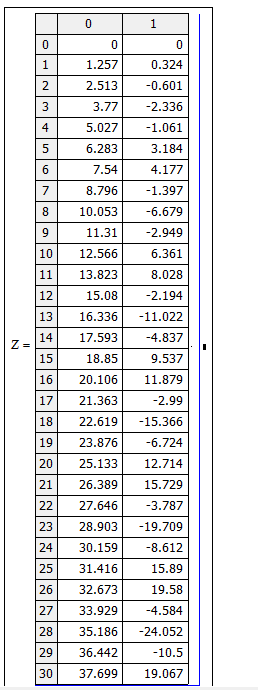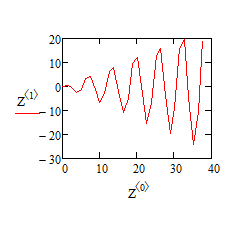



Выводы.

С помощью математического пакета Mathcad научился решать дифференциальные уравнения и строить их графики. Освоил технику работы с математическим пакетом MathCad.