Диффуры. Вариант№9. Решение дифференциального уравнения
 Скачать 50.58 Kb. Скачать 50.58 Kb.
|
|
Вариант №9 Задание №339 Найти общее решение дифференциального уравнения: 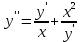 Решение: Данное уравнение является дифференциальным уравнением второго порядка допускающее понижение порядка. Так как в уравнение явно не входит функция 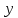 , то выполним замену переменной: , то выполним замену переменной: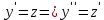  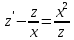 Это уравнение Бернулли. Умножим обе части уравнения на 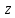 (при этом (при этом 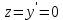 не является решением уравнения) не является решением уравнения)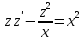 Выполним замену: 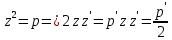 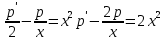 Получили линейное неоднородное уравнение первого порядка. Его решение будем искать в виде: 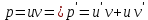 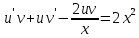  Выберем функцию  таким образом, чтобы выражение в скобках равнялось нулю: таким образом, чтобы выражение в скобках равнялось нулю: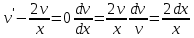 Интегрируем обе части уравнения: 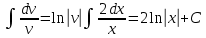 Выберем частное решение при 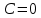 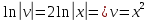 Подставим данное значение в уравнение (*): 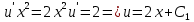  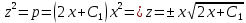 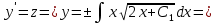 Выполним замену переменной:   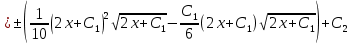 Задание №349 Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям: 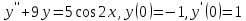 Решение: Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Найдем общее решение однородного уравнения: 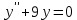 Составим и решим характеристическое уравнение: 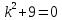 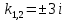 Корни характеристического уравнения комплексные сопряженные, поэтому общее решение однородного уравнения запишем в виде: 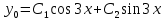 Найдем частное решение неоднородного уравнения. Правая часть уравнения является функцией специального вида с характеристическим числом  не совпадающим с корнями характеристического уравнения, поэтому частное решение неоднородного уравнения будем искать в виде: не совпадающим с корнями характеристического уравнения, поэтому частное решение неоднородного уравнения будем искать в виде: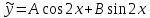 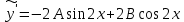  Подставим найденные значения в исходное уравнение: 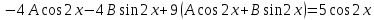 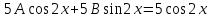 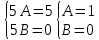 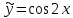 Общее решение уравнения запишем в виде: 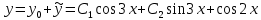 Найдем частное решение, удовлетворяющее начальным условиям:    Частное решение уравнения:  Задание №369 Точка массой 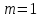 движется прямолинейно; на нее действует сила, пропорциональная времени, протекшему от момента, когда скорость равнялась нулю (коэффициент пропорциональности равен 2). Кроме того, точка испытывает сопротивление среды, пропорциональное скорости (коэффициент пропорциональности равен 3). Найти скорость в момент движется прямолинейно; на нее действует сила, пропорциональная времени, протекшему от момента, когда скорость равнялась нулю (коэффициент пропорциональности равен 2). Кроме того, точка испытывает сопротивление среды, пропорциональное скорости (коэффициент пропорциональности равен 3). Найти скорость в момент 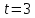 сек секРешение: Используем формулу: 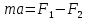 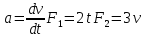 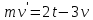 Учитывая, что 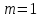 , получаем линейное неоднородное уравнение: , получаем линейное неоднородное уравнение: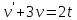 Найдем общее решение однородного уравнения: 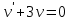 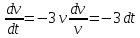 Интегрируем обе части уравнения: 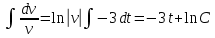  Решение неоднородного уравнения будем искать в виде:  Подставим данные значения в неоднородное уравнение:  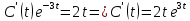  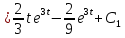 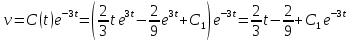 Найдем частное решение:  Частное решение: 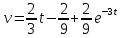 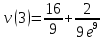 Задание №379 Вычислить с помощью двойного интеграла площадь фигуры, ограниченной указанными линиями. Сделать чертеж фигуры. 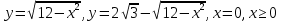 Решение: Площадь фигуры найдем по формуле: 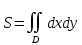 Построим область 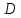 и опишем ее с помощью системы неравенств: и опишем ее с помощью системы неравенств: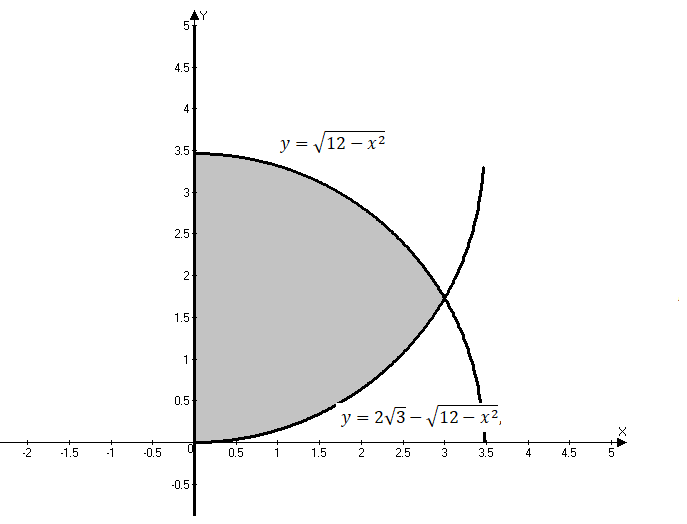 Найдем точки пересечения графиков функций: 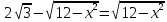 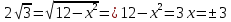 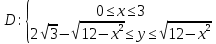  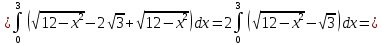 Используем значение табличного интеграла:   Задание №429 Исследовать сходимость числового ряда: 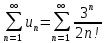 Решение: Это числовой знакоположительный ряд. Для его сходимости применим признак Даламбера: 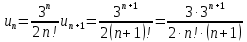  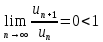 По признаку Даламбера ряд сходится. Задание №439 Найти интервал сходимости степенного ряда: 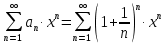 Решение: Радиус сходимости степенного ряда найдем по формуле: 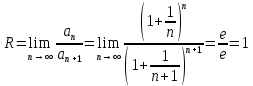 Ряд сходится абсолютно на интервале (-1;1) Исследуем ряд на сходимость на концах интервала:   Общий член ряда по модулю не стремится к нулю, поэтому по признаку Лейбница ряд сходится 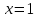 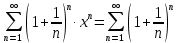 Не выполняется обязательный признак сходимости. Общий член ряда не стремится к нулю, поэтому ряд расходится.  Задание №469 Функция  задана в интервале (0;2). Разложить данную функцию в ряд Фурье в интервале (-2;2) продолжив ее в интервал (-2;0) четно. задана в интервале (0;2). Разложить данную функцию в ряд Фурье в интервале (-2;2) продолжив ее в интервал (-2;0) четно.Решение: Разложение функции в ряд Фурье на произвольном периоде 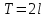 имеет вид: имеет вид: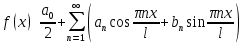 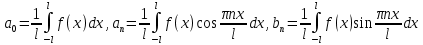 Продолжим функцию четным образом: 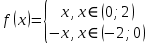 Тогда коэффициент 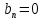  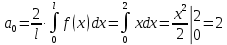 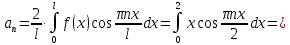 Применим формулу интегрирования по частям: 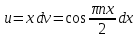 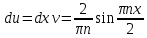 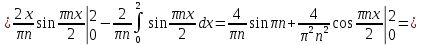 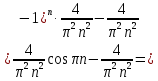 В итоге получаем: 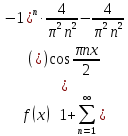 |
