Решение для 2 моделей. Модель линейного программирования Транспортная модель в отчетах для каждой из моделей должны быть
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
Санкт-Петербургский политехнический университет Петра Великого Институт промышленного менеджмента, экономики и торговли Применение моделей оптимизации по дисциплине «Математические методы в экономике и управлении» Выполнил студент гр.з3733801/90501 Е.И.Ульянова Руководитель доцент, к.ф.-м.н. А.Л. Кутузов «___» __________ 2022 г. Санкт-Петербург 2022 Санкт-Петербургский политехнический университет Петра Великого ЗАДАНИЕ НА ВЫПолнение студенту группы з3733801/90501 Ульяновой Еве Игоревне 1. Тема работы: Применение моделей оптимизации. 2. Срок сдачи студентом законченной работы _________ 3. Исходные данные к работе: 1) Теоретические материалы лекций. 2) Учебное пособие А.Л. Кутузов. Компьютерные методы экономического моделирования. – СПб.: Изд-во Политехн. ун-та, 2020 (доступно в электронном виде в информационно-библиотечном комплексе СПбПУ, далее – все ссылки на страницы и рисунки этого пособия). 3) Учебная литература и информация, представленная на сайтах. 4) Программное обеспечение MS Office. 4. Содержание пояснительной записки: номер варианта работы (номер студента в списке группы), основная часть, заключение, список использованных источников. В основной части с помощью программы Excel найдите оптимальное решение для 2 моделей. Модель линейного программирования Транспортная модель В отчетах для каждой из моделей должны быть: a. Словесное описание ситуации, обозначения переменных и алгебраическая формулировка задачи (примеры на стр. 5 и 26 для 1-й модели и 54 – для 2-й). Названия продуктов в 1-й модели и грузов во 2-й придумайте сами. b. Табличная модель (примеры на рис. 1.21, 1.22, 1.32 для 1-й модели и 3.16 – для 2-й). c. Окна «Поиска решения» – в зависимости от версии Excel (примеры на рис. 1.23, 1.26 или 1.24, 1.27 для 1-й модели и 3.17 или 3.18 – для 2-й,). d. Отчет об устойчивости (примеры на рис. 1.34 для 1-й модели и 3.19 – для 2-й ). Получив решение модели линейного программирования, ответьте на следующие вопросы: a. Каков оптимальный производственный план и какую прибыль он обеспечит? b. Как может меняться прибыльность отдельных продуктов, чтобы этот план оставался оптимальным? c. Какие ресурсы являются дефицитными? d. По какой цене и сколько их можно купить? Получив решение транспортной модели, ответьте на следующие вопросы: a. Каков оптимальный план перевозок и какие при нем будут общие транспортные расходы? b. Как нужно изменить тарифы тех перевозок, которые не вошли в оптимальный план, чтобы они стали выгодными? c. Как изменятся общие транспортные расходы, если снизить потребности в пунктах назначения? d. Как изменятся общие транспортные расходы, если увеличить запасы в пунктах отправления? ПРИМЕЧАНИЯ Подробный анализ результатов дан в пособии. Отвечая на вопросы, не переписывайте текст из пособия и не указывайте, где в отчете можно найти нужные ответы. На каждый вопрос приводите только конкретные числа. В копиях экранов с формулами (аналогичных рис. 1.21, 1.22 и 3.16), должны быть видны заголовки строк и столбцов. Денежные величины во всех моделях нужно представлять в денежном или финансовом формате (с указанием денежных единиц). Фон всех пустых ячеек по границам моделей сделайте темным (см, например, рис. 1.21). В исходных данных каждой модели добавьте число N к правой части всех ограничений (где N — номер студента в списке группы). Примерный объём пояснительной записки 10–20 страниц печатного текста. 5. Перечень графического материала: копии экранов, отображающие основные результаты работы (аналогичные рисункам, перечисленным выше, но с данными для своего варианты задания). 6. Консультанты________________ 7. Дата получения задания: «___» ____________ 20__ г. Руководитель ________________ А.Л. Кутузов Задание принял к исполнению _______________ И.И. Иванов ____________(дата) Оглавление1. ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 6 2. ТРАНСПОРТНАЯ ЗАДАЧА 13 1. ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯТребуется определить план выпуска четырех видов продукции, обеспечивающий максимальную прибыль от ее реализации. На изготовление этой продукции расходуются трудовые ресурсы, сырье и финансы. С учетом рыночного спроса и производственно-технологических возможностей заданы предельные границы выпуска каждого вида продукции. Эти границы, наличие и нормы расхода ресурсов, а также маржинальная прибыль (разность между выручкой и переменными издержками) на единицу продукции приведены в таблице:
Обозначив количество выпускаемых изделий через x1, x2,x3, x4, а целевую функцию (валовую маржинальную прибыль) — через F, построим математическую модель задачи: F = 120x1 + 110x2 + 160x3 + 190x4 max, 51x1 + 52x2 + 51x3 + 52x4 ≤ 69, 53 ≤ x1 ≤ 55, 57x1 + 54x2 + 55x3 + 54x4 ≤ 130, 51 ≤ x2, 55x1 + 57x2 + 59x3 + 58x4 ≤ 150, 51 ≤ x3 ≤ 53, 52≤x4 ≤54, x1, x2, x3, x4 ≥ 0. Три неравенства, расположенные слева, будем в дальнейшем называть ограничениями, а четыре справа — граничными условиями (они показывают, в каких пределах могут изменяться значения переменных). В последней строке модели находятся условия неотрицательности. Они говорят о том, что количество выпускаемых изделий не может быть отрицательным. Так как такие условия присутствуют в большинстве моделей линейного программирования, мы привели их здесь для общности, хотя в данной задаче неотрицательность переменных вытекает из граничных условий. В результате этих преобразований каждое ограничение должно содержать только один знак неравенства. Слева от него — переменные с коэффициентами, справа — числа. (Не должно быть чисел слева от знака неравенства или переменных — справа.) Нахождение одинаковых переменных в одном столбце поможет заполнению соответствующих столбцов электронной таблицы. F = 120x1 + 110x2 + 160x3 + 190x4 max, 51x1 + 52x2 + 51x3 + 52x4 ≤ 69 57x1 + 54x2 + 55x3 + 54x4 ≤ 130 55x1 + 57x2 + 59x3 + 58x4 ≤ 150 x1 ≤ 55 x3 ≤ 53 x4 ≤54 x1 ≥ 53 x2 ≥ 51 x3 ≥ 51 x4 ≥ 52 x1, x2, x3, x4 ≥ 0. Руководствуясь этой алгебраической формой модели, введем на лист Excel числовые данные (рис. 1). При этом условия неотрицательности переменных вводить не нужно, так как они задаются с помощью соответствующего параметра средства Поиск решения. В первой строке таблицы располагается заголовок, во второй — наименования продуктов. Третья строка отведена для значений переменных, которые после вычислений появится в ячейках B3:E3, выделенных с помощью рамки, образованной внешней границей ячеек. Можно, конечно, оставить эти ячейки пустыми, но лучше ввести какие-нибудь небольшие числа, например единицы, которые позволят проверить правильность вводимых формул (будут видны отличные от нуля результаты вычислений). В четвертой строке в ячейках B4:E4 заданы коэффициенты целевой функции, а ячейка F4, выделенная внешней границей и цветом заливки, зарезервирована для вычисления значения целевой функции. Строки с 6-й по 15-ю содержат коэффициенты, знаки и правые части ограничений. В столбце Лев.часть будут вычисляться левые части ограничений, а в столбце Разница — разность правых и левых частей. 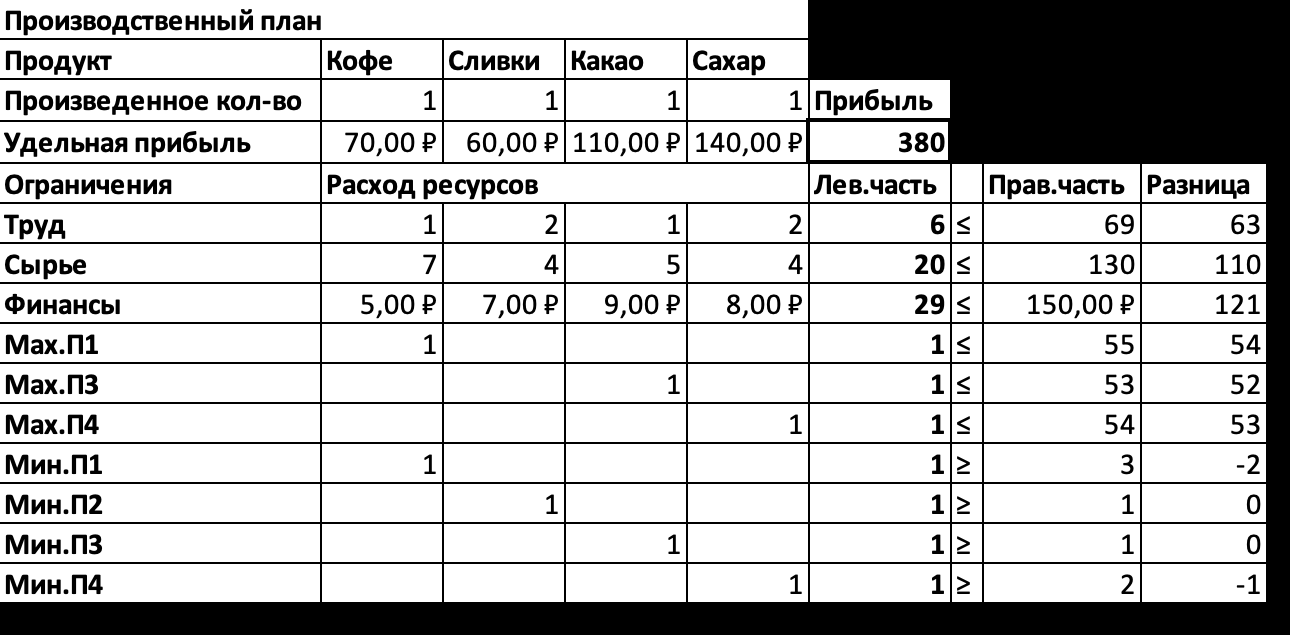 Рисунок 1 Предложенная форма таблицы удобна для выполнения расчетов, анализа результатов и документирования модели. Наглядность обеспечивается соответствующим форматированием: использованием заголовков, жирного шрифта, подчеркивания текста, рамок по границам ячеек, выделения цветом и различных видов выравнивания. Чтобы задокументировать созданную модель, нужно сохранить ее изображение не только с числами, как на рис. 1, но и с формулами (рис. 2). 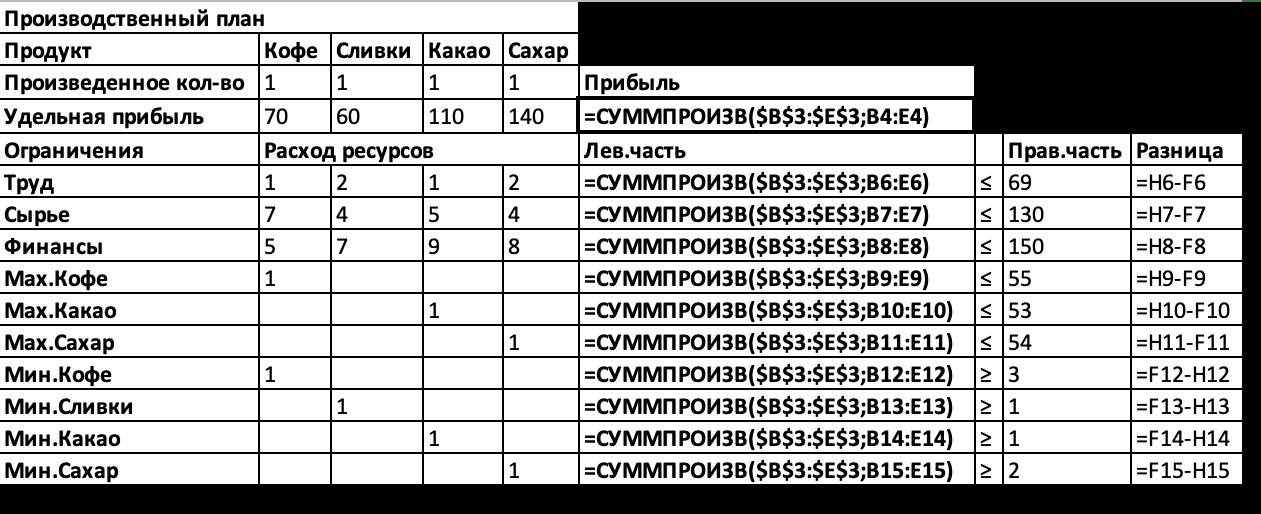 Рисунок 2 На рис. 3 показано использование имен диапазонов в формулах модели. Это позволяет сделать формулы понятнее.  Рисунок 3 На рис. 4 показано, как на листе выглядят результаты вычислений. В ячейках B3:E3 выводится оптимальный производственный план, в ячейке F4 — получаемая максимальная прибыль. 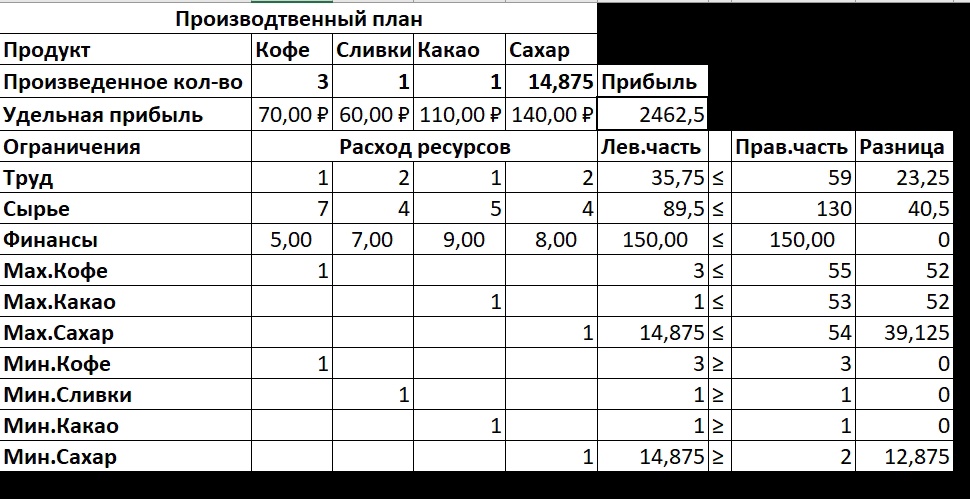 Рисунок 4 а)В строках 6–8, содержащих ограничения на ресурсы, в столбце Лев.часть — количество использованных ресурсов, а в столбце Разница — их остаток после выполнения оптимального плана. Разница финансов равна нулю, то есть этот ресурс будет использован полностью, то есть является дефицитным. В строках 9–15, содержащих граничные условия, в столбце Лев.часть — значения переменных в оптимальном решении, а в столбце Разница — разность между этими значениями и заданными для переменных верхними или нижними границами. Если разница равна нулю, то соответствующая переменная принимает свое граничное значение. В нашем случае это переменные Мин.Кофе, Мин.Сливки и Мин.Какао. Вызов средства Поиск решения Окно параметры поиска решений (рис.5). 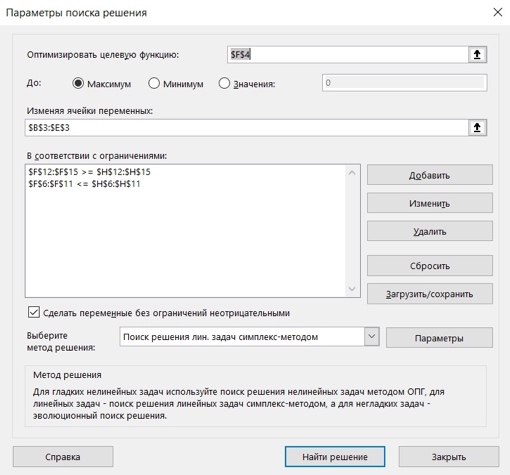 Рисунок 5 Дополнительные параметры поиска решения в Excel 2010 (или новее) (рис.6).  Рисунок 6 Отчет об устойчивости (рис.7) содержит основную информацию для анализа чувствительности модели. Этот отчет показывает, насколько чувствительно найденное решение к изменениям параметров модели (коэффициентов целевой функции и правых частей ограничений). При этом предполагается, что значения всех параметров, за исключением какого-то одного, остаются неизменными. 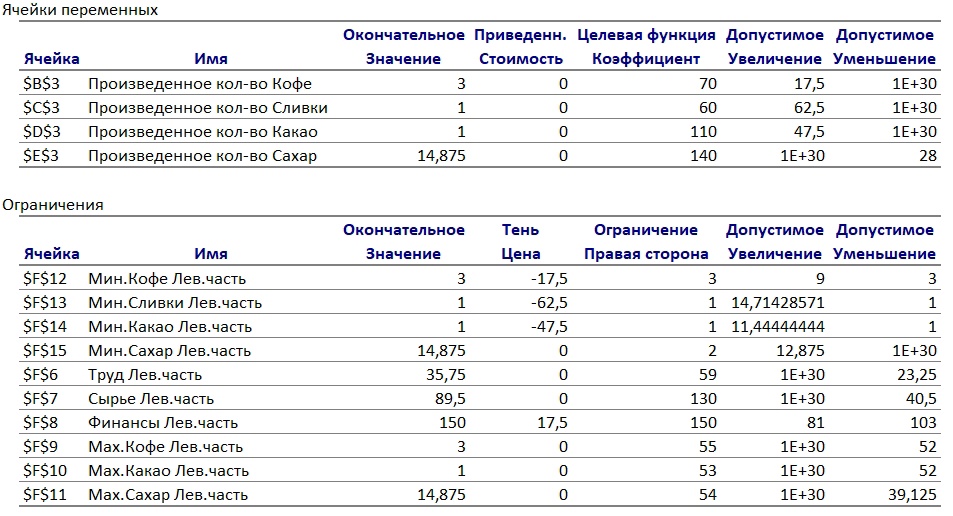 Рисунок 7 Ответы на вопросы: Каков оптимальный производственный план и какую прибыль он обеспечит? Оптимальный производственный план предполагает производство 3 единиц Кофе, 1 единицы Сливок, 1 единицы Какао, 14,875 единиц Сахара. Данный производственный план обеспечит прибыль в размере 2462,5 руб. Как может меняться прибыльность отдельных продуктов, чтобы этот план оставался оптимальным? Интервалом оптимальности для Кофе является (3;9], для Сливок - (1; 14,714], для Какао - (1; 11,444], для Сахара – [14,875; 1Е+30). Какие ресурсы являются дефицитными? Дефицитным ресурсом являются финансы, так как их теневая цена отлична от 0 (17,5). d. По какой цене и сколько их можно купить? Финансы можно купить (занять) по цене 17,5 руб. за 1 руб. полученных финансов. Можно приобрести дополнительно 103 руб. финансов. 2. ТРАНСПОРТНАЯ ЗАДАЧА |
