НИРС Кузнецов. Решение Для каждого человека принятие решений полностью индивидуально и не существует готового алгоритма принятия решений, подходящего всем. Обычно умение принимать решения вырабатывается с опытом
 Скачать 1.19 Mb. Скачать 1.19 Mb.
|
1 2 Этап 5На пятом этапе проектируется реализация выбранной альтернативы 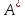 , которая становится целью системы - , которая становится целью системы - 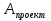 . Сравнение проектной альтернативы . Сравнение проектной альтернативы 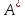 и фактического состояния системы и фактического состояния системы 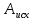 позволяет установить отклонения по каждому базовому критерию. После ввода дополнительных ограничений («трудоемкости» изменения локальных критериев позволяет установить отклонения по каждому базовому критерию. После ввода дополнительных ограничений («трудоемкости» изменения локальных критериев 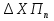 , приоритета возможных изменений подкритериев) выбирается решение, минимизирующее целевую функцию L (либо максимизирующее функцию , приоритета возможных изменений подкритериев) выбирается решение, минимизирующее целевую функцию L (либо максимизирующее функцию 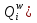 . .Для реализации варианта составляется программа практических мероприятий, которая приводит к улучшению базовых характеристик системы, при целенаправленном изменении локальных параметров. Метод анализа иерархий. Метод анализа иерархий является систематической процедурой для иерархического представления элементов, определяющих суть любой проблемы. Метод состоит в декомпозиции проблемы на все более простые составляющие части и дальнейшей обработке последовательности суждений лица, принимающего решение (ЛПР), по парным сравнениям. В результате может быть выражена относительная степень (интенсивность) взаимодействия элементов в иерархии. Эти суждения затем выражаются численно. Метод анализа иерархии включает процедуры синтеза множественных суждений, получения приоритетности критериев и нахождения альтернативных решений. Полезно отметить, что полученные таким образом значения являются оценками в шкале отношений и соответствуют так называемым жестким оценкам. Решение проблемы есть процесс поэтапного установления приоритетов. Весь процесс подвергается проверке и переосмысливанию до тех пор, пока не будет уверенности, что процесс охватил все важные характеристики, необходимые для представления и решения проблемы. Принцип идентичности и декомпозиции Принцип идентичности и декомпозиции предусматривает структурирование проблем, в виде иерархий или сети, что является первым этапом применения МАИ. В наиболее элементарном виде иерархия строится с вершины (целей — с точки зрения управления), через промежуточные уровни (критерии, от которых зависят последующие уровни) к самому низкому уровню (который обычно является перечнем альтернатив). Принцип дискриминации и сравнительных суждений После иерархического или сетевого воспроизведения проблемы возникает вопрос: как установить приоритеты критериев и оценить каждую из альтернатив по критериям, выявив самую важную из них? Парные сравнения В МАИ элементы задачи сравниваются попарно по отношению к их воздействию («весу», или «интенсивности») на общую для них характеристику. Проведем парные сравнения, приводящие к матричной форме — квадратной таблице, в которой числа могут быть расположены следующим образом:  Скобки, в которые заключена матрица размерностью 4X4 используются для обозначения стандартной формы матрицы. Сравнивая набор составляющих проблемы друг с другом, получаем следующую квадратную матрицу: 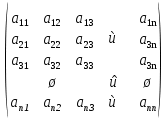 Очевидно, что эта матрица имеет свойства обратной симметричности: 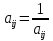 где индексы i и j относятся к строке и столбцу соответственно. Пусть А1, A2, А3, ..., Ап — множество из п элементов и w1,w2, w3, ..., wn — соответственно их веса, или интенсивности. С использованием МАИ сравним вес, или интенсивность, каждого элемента с весом, или интенсивностью, любого другого элемента множества по отношению к общему для них свойству или цели. Сравнение весов можно представить следующим образом:  Отметим, что матрица может состоять только из одной строки или одного столбца, которые называются векторами. Квадратная матрица имеет равное число строк и столбцов, а также другие полезные характеристики, такие, как собственные векторы и собственные значения. Альтернативы: К1- Кислород (O2) + водород; Iy.п = 4541 м/с ρ = 0,3155 г/см3 К2- Кислород + керосин; Iy.п = 3599 м/с ρ = 1,036 г/см3 К3- Кислород + НДМГ (C2H8N2); Iy.п = 3720 м/с ρ = 0,9915 г/см3 К4- Кислород + гидразин (N2H4); Iy.п = 3394 м/с ρ = 1,0715 г/см3 К5- Кислород + аммиак (NH3); Iy.п = 3168 м/с ρ = 0,8393 г/см3 К6- АТ (N2O4) + керосин; Iy.п = 3308 м/с ρ = 1,269 г/см3 К7- АТ + НДМГ (C2H8N2); Iy.п = 3403 м/с ρ = 1,185 г/см3 К8- АТ + гидразин (N2H4); Iy.п = 3425 м/с ρ = 1,228 г/см3 Критерии:
В основе метода лежит линейная свертка, но оценки альтернатив и веса критериев получаются особым образом. В модели АНР вместо критериальной таблицы принята иерархия. Представим ее следующим образом: Уровень 0 : Цель – выбор топлива для носителей, выводящих аппараты на лунную орбиту. Уровень 1: Критерии - – максимальный удельный импульс –минимальная масса конструкции топливных баков – экономичность топлива Уровней может быть сколько угодно. Критерий 1-го уровня "экономичность" можно раскрыть уровнем 2 как: 1) расход топлива, 2) качество топлива, 3) стоимость топлива, 4) экологичность топлива. Получим оценки каждой альтернативы по каждому критерию. Если существуют объективные оценки, то они просто выписываются и нормируются таким образом, чтобы их сумма была равна единице. С таким критерием как "экономичность топлива", для которого не существует объективных оценок, процедура Саати рекомендует использовать парные сравнения. Для фиксации результата сравнения пары альтернатив может использоваться, например, шкала следующего типа: 1 – проигрывает в сравнении, 2 – равноценны, 4 – выигрывает в сравнении. Результат парных сравнений альтернатив для критерия "максимальный удельный импульс" записывается в виде таблицы: Таблица 3. Результат парных сравнений альтернатив для критерия "максимальный удельный импульс"
Суммы нормируются образом, чтобы итог был равен 1. Для этого разделим сумму каждой строки на 150 (сумма последнего столбца, т.е. сумма самих строчных сумм). Получим: Таблица 4. Результат парных сравнений альтернатив для критерия "максимальный удельный импульс"
Аналогично построим таблицу для критерия «минимальная масса конструкции топливных баков»: Таблица 5. Результат парных сравнений альтернатив для критерия "минимальная масса конструкции топливных баков"
И точно также построим таблицу для критерия «экономичность топлива»: Таблица 6. Результат парных сравнений альтернатив для критерия "экономичность топлива"
Стоит отметить, что полученные оценки отражают исключительно точку зрения конкретного лица, принимающего решение. На самом деле, вместо строчных сумм Саати рекомендует использовать собственный вектор матрицы парных сравнений, считая его более точной оценкой. Но для простоты ограничимся только строчными суммами, которые допустимы, но, с точки зрения Саати, менее точны. Аналогичным образом получаются веса критериев. Сравним попарно критерии с точки зрения их сравнительной важности. Запишем результаты сравнений в виде таблицы.
Таблица 7. Результат парных сравнений критериев Таким образом, мы получили веса критериев Занесем в таблицу оценки альтернатив по критериям: Таблица 8. Результат оценки альтернатив по критериям
Далее, применяя линейную свертку (взвешенную сумму), получим следующие интегральные оценки альтернатив (функция полезности): Таблица 9. Функция полезности
Вывод:Таким образом, процедура рекомендует выбрать К1- Кислород (O2) + водород Главным достоинством процедуры считается тот факт, что веса критериев и оценки по субъективным критериям не назначаются прямым волевым методом (как чаще всего пытаются делать, не сильно задумываясь о корректности такого волюнтаризма), а на основе парных сравнений. При этом остается неопределенным (интуитивным) понятие "превосходство" одного критерия над другим. Серьезные исследования последнего десятилетия приводят к выводу, что корректнее и надежнее использовать парные сравнения для получения только качественных заключений, типа: "критерий К1 важнее критерия К2", не уточняя на сколько важнее. Другое достоинство - представление критериев в виде иерархии (дерева). Используя одну критериальную таблицу (один уровень), мы упрощаем ситуацию, выполняя оценку либо для верхних уровней дерева критериев, либо для самых нижних Для примерной оценки это подойдет, но при оценке более сложных альтернатив полезнее использовать все дерево критериев. Метод Саати-Кернса (Метод аналитического планирования) Для данного метода потребуется 4 матрицы – 1 для второго уровня (попарного сравнения «важности» критериев между собой; такая матрица, впрочем, представлена в предыдущем пункте) и 3 для заданной цели – выбора топлива. Шкала сравнения Саати в данном методе такова:
Важное отличие этого метода состоит в том, что в матрице имеют место обратные величины; если, например, при сравнении первого критерия со вторым мы получили число «3», то при обратном сравнении (второго с первым) получим обратное число – т.е. «1/3». Матрица попарных сравнений для уровня 2 Таблица 10. Матрица попарных сравнений
Матрица для критерия «Максимальный удельный импульс» Таблица 11. Матрица для критерия «Максимальный удельный импульс»
Матрица для критерия «Минимальная масса конструкции топливных баков» Таблица 12. Матрица для критерия «Минимальная масса конструкции топливных баков»
Матрица для критерия «Экономичность топлива» Таблица 13. Матрица для критерия «Экономичность топлива»
Результат оценки альтернатив по критериям Таблица 14. Результат оценки по критериям
Интегральные взвешенные оценки альтернатив Таблица 13. Интегральные взвешенные оценки
Вывод: Используя данный критерий оценки, получено, что предпочтение следует отдать К2- Кислород + керосин, так как она имеет наибольшее значение в векторе приоритетов (см. табл. 13). Можно отметить, что решение проблемы выбора топлива есть процесс поэтапного установления приоритетов. На первом этапе выявляются наиболее важные элементы проблемы, на втором – наилучший способ проверки наблюдений, испытания и оценки элементов, следующим этапом может быть выработка способа применения решения и оценка его качества. Весь процесс подвергается проверке и переосмысливанию до тех пор, пока не будет уверенности, что процесс охватил все важные характеристики, необходимые для представления и решении проблемы. Если интуиция и субъективные оценки являются основными исходным материалом, на основании которого индивидуум получает ясно представление о своих творческих способностях, то суждение о превосходстве одного элемента над другим и интенсивность этих суждений можно использовать для выражения внутренних чувств и склонностей. Суждения расширяют рамки общения, укрупняя кластеры и элементы, имеющиеся в иерархии по определенной проблеме. Заключение В работе даны определения ключевых понятий тории принятия решений. Сделан обзор общего метода принятия решений в условиях неопределенности Проведена работа по выбору альтернативы в условиях неопределенности по заданным критериям. Были выбраны следующие альтернативы: К1- Кислород (O2) + водород; К2- Кислород + керосин; К3- Кислород + НДМГ (C2H8N2);К4- Кислород + гидразин (N2H4); К5- Кислород + аммиак (NH3); К6- АТ (N2O4) + керосин; К7- АТ + НДМГ (C2H8N2); К8- АТ + гидразин (N2H4); Список литературы
1 2 |
